Next: Time Series Analysis of Unequally Spaced Data: Intercomparison Between Estimators of the Power Spectrum
Previous: Unified Survey of Fourier Synthesis Methodologies
Up: Algorithms
Table of Contents - Index - PS reprint - PDF reprint
V. L. Oknyanskij
Sternberg Astronomical Institute, Universitetskij Prospekt 13, Moscow, 119899, Russia
Radio-optical variability correlation in Q0957+561 was first reported
by Oknyanskij & Beskin (1993, hereafter OB) on the basis of radio
observations made in the years 1979 to 1990. OB used an idea to take
into account the known gravitational lensing time delay to get
combined radio and optical light curves and then to use them for
determination of the possible radio-from-optical time delay. It was
found this way that radio variations (5MHz) followed optical ones
by about 6.4 years with high level of correlation (![]() 0.87).
Using new radio data (Haarsma et al. 1997), for the interval 1979-1994,
we find nearly the same value for the optical-to-radio delay as had
been found before. Additionally, we suspect that the time delay value
is linearly increasing at about 110 days per year while the portion
of reradiated flux in the radio response is decreasing.
0.87).
Using new radio data (Haarsma et al. 1997), for the interval 1979-1994,
we find nearly the same value for the optical-to-radio delay as had
been found before. Additionally, we suspect that the time delay value
is linearly increasing at about 110 days per year while the portion
of reradiated flux in the radio response is decreasing.
We conclude that the variable radio source is ejected from the central part of the QSO compact component.
Time delay determinations in astrophysics are used most often to
find time shifts between variations in different spectral bands and/or
lines in AGNs, as well as time delays between different
images of gravitationally lensed QSOs. In most cases, the task
is complicated by uneven spacing of data, so that standard
cross-correlation methods become useless. Two different methods
are most often used: CCF (Gaskell & Spark 1986) and DCF (Edelson &
Krolik 1988), which are based on line interpolation of
data sets or binning of correlation coefficients,
respectively. We have introduced
several simple improvements to CCF (Oknyanskij 1994) and this
modernized MCCF combines the best properties of CCF and DCF
methods. With MMCF we calculated regression
coefficients as functions of time shift. Here,
this calculation is
generalized for the more complex case where the time delay is a
linear function of time, and a portion of the flux density is
itself a power-law function of the delay. We apply this method to
the optical-to-radio time delay in the gravitationally lensed double quasar
Q0957+561.
The data sets used here were obtained to determine the
gravitational lensing time delay ![]() o.
Our results are nearly identical
for values of
o.
Our results are nearly identical
for values of ![]() o
in the interval of 410-550 days.
In the
discussion below, we take
o
in the interval of 410-550 days.
In the
discussion below, we take ![]() o=425 days.
o=425 days.
Our method includes several steps, which are briefly explained below:
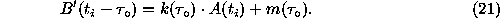
We combine these values B´ with the usual B ones, sorting by time. The resulting optical light curve was then smoothed by averaging in 200 day intervals with steps of 30 days. This accounts for the physical argument that radio sources should be bigger than optical ones. The value of 200 days for smoothing was taken as about optimal from the autocorrelation analysis of light curves.
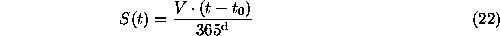
to be added to dates in the optical light curves:

Assuming that a portion of radio flux decreases as
a power-law function of time with exponent ![]() .
We should also correct the
optical flux for that fading before computing the cross-correlation
function:
.
We should also correct the
optical flux for that fading before computing the cross-correlation
function:
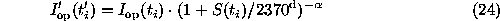
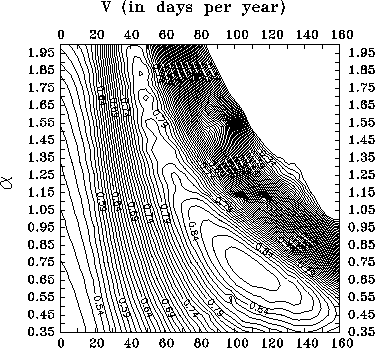
Figure: Two-dimensional cross-correlation function (see text).
Original PostScript figure (192kB).
For points (V,![]() )
we map the MCCF values
(see Figure 1).
The best correlation
occurs for V
)
we map the MCCF values
(see Figure 1).
The best correlation
occurs for V![]() 100
days/year, and
100
days/year, and ![]()
![]() 0.7.
0.7.
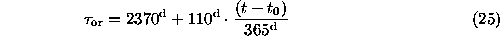
We have calculated the time delay between radio and optical flux variations using a new method. In addition, we have investigated the possibilities that (1) there is a change of the time delay that is a linear function of time, and (2) the radio response has power-law dependence on the time delay value.
Finally, let us stress some additional consequences from our results:
Figure: Radio and optical combined light curves.
(The optical light curve is corrected as described in the text.)
Original PostScript figure (168kB).
In conclusion, we thank Debborah Haarsma for sending us the preprint with the new radio data for Q0957+561 before publication.
Edelson, R. A., & Krolik, J. H. 1988, ApJ, 333, 646
Gaskell, C. M., & Spark, L. S. 1986, ApJ, 305, 175
Haarsma, D. B., Hewitt, J. N., Lehar, J., & Burke, B. F. 1997, ApJ, 479, 102
Oknyanskij, V. L., & Beskin, G. M. 1993, in Gravitational Lenses in the Universe: Proceedings of the 31st Liege International Astrophysical Colloquium, eds. J. Surdej et al. (Liege, Belgium: Universite de Liege, Institut d'Astrophysique), 65
Oknyanskij, V. L. 1994, Ap&SS, 222, 157
Schild, R. E., & Thomson, D. J. 1995, AJ, 109, 1970
Vanderriest, C., et al. 1989, A&A, 215, 1
Next: Time Series Analysis of Unequally Spaced Data: Intercomparison Between Estimators of the Power Spectrum
Previous: Unified Survey of Fourier Synthesis Methodologies
Up: Algorithms
Table of Contents - Index - PS reprint - PDF reprint