Next: Determination of Variable Time Delay in Uneven Data Sets
Previous: A Computer-Based Technique for Automatic Description and
Classification of Newly-Observed Data
Up: Algorithms
Table of Contents - Index - PS reprint - PDF reprint
Astronomical Data Analysis Software and Systems VI
ASP Conference Series, Vol. 125, 1997
Editors: Gareth Hunt and H. E. Payne
P. Maréchal, E. Anterrieu, and A. Lannes
Laboratoire d'Astrophysique and CERFACS,
Observatoire Midi-Pyrénées,
14, Avenue Édouard Belin F-31400 Toulouse (France)
Abstract:
This paper deals with theoretical and practical results
on aperture synthesis. Full attention is devoted to the
Fourier synthesis operation, which proves to be the
central issue with regard to the global problem.
Different regularization techniques are shown to derive
from a unique principle:
the Principle of Maximum Entropy on the Mean (PMEM).
This is the case for WIPE|, as well as for the traditional
Maximum Entropy Method (and for some others).
In order to compare the performances of different regularizers,
some numerical simulations are presented.
Let 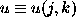 denote the spatial frequency
corresponding to the baseline
denote the spatial frequency
corresponding to the baseline 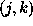 of the
interferometric device, and let
of the
interferometric device, and let 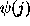 be the aberration phase
term of pupil element j .
The central problem is to reconstruct both the brightness distribution
be the aberration phase
term of pupil element j .
The central problem is to reconstruct both the brightness distribution 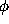 (of some object) and the pupil phase function
(of some object) and the pupil phase function 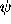 , by using as data
complex-visibility measurements of the form
, by using as data
complex-visibility measurements of the form 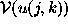 .
The latter are related to
.
The latter are related to 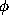 and
and 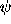 by the equation
by the equation
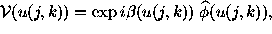 in which
in which 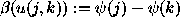 and
and 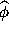 is the Fourier transform of
is the Fourier transform of 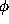 . Solving for
. Solving for 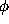 (assuming that
(assuming that 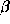 is known) is a Fourier synthesis operation, while solving for
is known) is a Fourier synthesis operation, while solving for 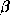 corresponds to a phase calibration operation. The whole problem
must be solved in such a way that the solution is not too sensitive to
unavoidable measurement errors. In other words, the inverse problem
under consideration must be regularized, and it is essential that the chosen
methodology provides an estimation of the reconstruction stability. In fact, the Fourier
synthesis operation proves to be the core of the problem. It has the form
of a linear inverse problem. The corresponding ``measurement equation''
may be written as
y = A x,
in which
corresponds to a phase calibration operation. The whole problem
must be solved in such a way that the solution is not too sensitive to
unavoidable measurement errors. In other words, the inverse problem
under consideration must be regularized, and it is essential that the chosen
methodology provides an estimation of the reconstruction stability. In fact, the Fourier
synthesis operation proves to be the core of the problem. It has the form
of a linear inverse problem. The corresponding ``measurement equation''
may be written as
y = A x,
in which 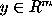 is the real-valued data vector associated with
is the real-valued data vector associated with
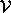 , A is the Fourier sampling operator, and x is the
vector formed with the components of
, A is the Fourier sampling operator, and x is the
vector formed with the components of 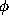 in an adequate basis
(Maréchal & Lannes 1996).
in an adequate basis
(Maréchal & Lannes 1996).
In practice, equation y = A x
fails to have a unique and stable solution,
and is therefore replaced by an optimization problem of the form
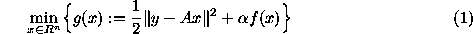
in which f is a measure of roughness of x ,
and 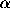 is the so-called regularization parameter. The
quadratic term in (1) forces the object to fit the data, while
the regularization term stabilizes the solution with respect to
small variations in y (and of course ensures uniqueness).
Denoting by
is the so-called regularization parameter. The
quadratic term in (1) forces the object to fit the data, while
the regularization term stabilizes the solution with respect to
small variations in y (and of course ensures uniqueness).
Denoting by 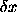 the variation of the solution
the variation of the solution 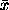 induced by a variation
induced by a variation 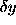 , the stability is
governed by an inequality such as
, the stability is
governed by an inequality such as

The trade-off between fitting the data and stability depends in a crucial manner
on the nature of f and on the value of 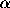 .
We emphasize that the regularization term should also
be designed so that g has a physical meaning, so that
the solution
.
We emphasize that the regularization term should also
be designed so that g has a physical meaning, so that
the solution 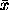 can be easily interpreted.
can be easily interpreted.
Let us now review some classical examples. The well-known Tikhonov
regularization corresponds to the case 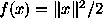 .
It can be generalized by choosing
.
It can be generalized by choosing
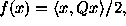 in which Q is a symmetric non-negative n × n matrix.
When x can be interpreted as a (discrete) probability density,
one often takes the Shannon entropy
in which Q is a symmetric non-negative n × n matrix.
When x can be interpreted as a (discrete) probability density,
one often takes the Shannon entropy 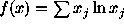 or
the Kullback measure
or
the Kullback measure
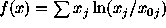 ,
in which
,
in which
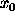 represents a prior knowledge of the object. If x is
only assumed to be positive, one can use the Generalized
Cross-Entropy (GCE)
represents a prior knowledge of the object. If x is
only assumed to be positive, one can use the Generalized
Cross-Entropy (GCE)
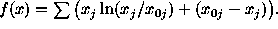 Let us also mention the Itakura-Saito criterion
Let us also mention the Itakura-Saito criterion
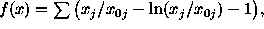 frequently used in spectral analysis.
frequently used in spectral analysis.
Recently, a new Fourier synthesis method has been
developed for radio imaging and optical interferometry (Lannes,
Anterrieu, & Bouyoucef 1994, 1996; Lannes, Anterrieu, & Maréchal
1997):
WIPE|. The name
of WIPE| is associated with that of ÇLEAN|.
To some extent (Lannes, Anterrieu, & Maréchal 1997),
WIPE| can be regarded as an updated version of ÇLEAN|.
In particular, the robustness of the
reconstruction process is well controlled.
The main aspects of WIPE| are its regularization principle
(for controlling the image resolution)
and its matching pursuit strategy (for constructing the image support).
The regularizer of WIPE|
is defined by the relation
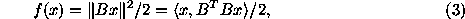
in which
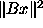 represents the energy of x
in the high frequency band (Lannes,
Anterrieu, & Bouyoucef 1994).
Clearly, this regularization principle belongs to the Tikhonov family, since
represents the energy of x
in the high frequency band (Lannes,
Anterrieu, & Bouyoucef 1994).
Clearly, this regularization principle belongs to the Tikhonov family, since
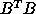 is a symmetric non-negative n × n matrix. It is very
closely related to the notion of resolution. The function to be minimized in (1)
takes the form
is a symmetric non-negative n × n matrix. It is very
closely related to the notion of resolution. The function to be minimized in (1)
takes the form 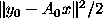 with
with 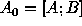 and
and 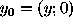 .
This kind of function is efficiently minimized by a conjugate-gradients
algorithm, which has the advantage of providing (with negligible
additional computing time) an estimate of the condition number and, thereby,
control of the stability of the reconstruction process.
As for the matching pursuit strategy, we simply mention that the
main difference from ÇLEAN| is that it can be conducted
at the level of the scaling functions of the object workspace (Lannes,
Anterrieu, & Bouyoucef 1994)
.
This kind of function is efficiently minimized by a conjugate-gradients
algorithm, which has the advantage of providing (with negligible
additional computing time) an estimate of the condition number and, thereby,
control of the stability of the reconstruction process.
As for the matching pursuit strategy, we simply mention that the
main difference from ÇLEAN| is that it can be conducted
at the level of the scaling functions of the object workspace (Lannes,
Anterrieu, & Bouyoucef 1994)
We now turn to the unification of WIPE| with
the methodologies mentioned in § 2 by the
Principle of Maximum Entropy on the Mean. Note first
that the optimization problem (1) is equivalent to
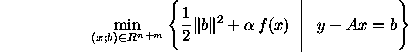
in which we have explicitly introduced the error term b .
In the PMEM, 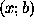 is a random vector
to which a prior probability measure
is a random vector
to which a prior probability measure 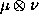 is assigned.
The Maximum Entropy Principle is then used to infer a posterior
probability on
is assigned.
The Maximum Entropy Principle is then used to infer a posterior
probability on 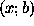 , and finally, we choose the expectancy
of x under the inferred density
, and finally, we choose the expectancy
of x under the inferred density 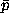 as the solution
to our inverse problem. The core of the PMEM is an
infinite dimensional linearly constrained optimization problem
(Maréchal & Lannes 1996)
in which the functional to be minimized is (the continuous version of)
the Kullback information measure. As explicitly
shown in Maréchal & Lannes (1996), it can be solved by means of a dual strategy. It is then possible
to demonstrate that, for particular choices of the priors
as the solution
to our inverse problem. The core of the PMEM is an
infinite dimensional linearly constrained optimization problem
(Maréchal & Lannes 1996)
in which the functional to be minimized is (the continuous version of)
the Kullback information measure. As explicitly
shown in Maréchal & Lannes (1996), it can be solved by means of a dual strategy. It is then possible
to demonstrate that, for particular choices of the priors 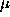 and
and  ,
the PMEM
gives rise to some of the most classical regularization techniques.
For example, a
Gaussian
,
the PMEM
gives rise to some of the most classical regularization techniques.
For example, a
Gaussian  with
with 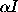 as the covariance matrix, associated with
a Gaussian
as the covariance matrix, associated with
a Gaussian 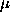 with covariance Q , gives rise to a Tikhonov regularization technique.
In particular,
if
with covariance Q , gives rise to a Tikhonov regularization technique.
In particular,
if 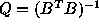 (provided that
(provided that 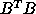 is positive definite),
we retrieve
WIPE|. Now, taking the multidimensional Poissonian distribution with vector
parameter
is positive definite),
we retrieve
WIPE|. Now, taking the multidimensional Poissonian distribution with vector
parameter 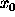 as
as 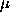 yields the GCE regularizer (Lannes,
Anterrieu, & Bouyoucef 1994),
and the Gamma law
with vector parameter
yields the GCE regularizer (Lannes,
Anterrieu, & Bouyoucef 1994),
and the Gamma law
with vector parameter 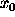 gives rise to the Itakura-Saito criterion.
Note that in this description, the quadratic fit term derives
from the standard Gaussian
prior measure on b . If another kind of noise were to corrupt the data,
this prior may, of course, be replaced by the appropriate one.
gives rise to the Itakura-Saito criterion.
Note that in this description, the quadratic fit term derives
from the standard Gaussian
prior measure on b . If another kind of noise were to corrupt the data,
this prior may, of course, be replaced by the appropriate one.
Many other criteria could be derived from the above scheme, taking into account
the probabilistic description of the problem. However, it is important
to keep in mind
that the design of f (i.e., the choice of the corresponding 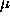 )
must be governed
by the nature of the imaging operator A . The next paragraph illustrates the
importance of this point.
)
must be governed
by the nature of the imaging operator A . The next paragraph illustrates the
importance of this point.
In the simulations presented here, the frequency coverage consists
of 211 points.
The object to be reconstructed, shown in Figure 1(a), is
the original object convolved by a point-spread function corresponding
to the selected resolution limit
(i.e., to the corresponding frequency coverage to be synthesized; see
Lannes, Anterrieu, & Bouyoucef 1994).
Three reconstructions
were performed: with WIPE| (Figure 1(b)), the Shannon entropy on the support
determined by the matching pursuit strategy of WIPE| (Figure 2(a)), and the GCE
in which the prior model 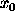 is a smoothed (and normalized) version of the
characteristic function of the previous support (Figure 2(b)). For the Shannon entropy
and the GCE, the regularization parameter
is a smoothed (and normalized) version of the
characteristic function of the previous support (Figure 2(b)). For the Shannon entropy
and the GCE, the regularization parameter 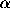 was adjusted in such a way that the final
fit term is equal to that reached by WIPE|.
The best reconstructed images, shown in Figures 1(b) and 2(b), are quite similar,
the values of the stability parameter
was adjusted in such a way that the final
fit term is equal to that reached by WIPE|.
The best reconstructed images, shown in Figures 1(b) and 2(b), are quite similar,
the values of the stability parameter 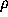 being reasonably small. In both cases,
the inverse problem is well regularized.
However, for the selected resolution,
the best stability is obtained with the WIPE| regularizer.
being reasonably small. In both cases,
the inverse problem is well regularized.
However, for the selected resolution,
the best stability is obtained with the WIPE| regularizer.
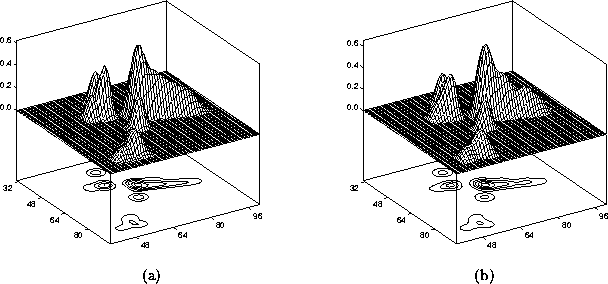
Figure:
a: image to be reconstructed;
b: reconstructed image by WIPE| (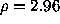 ).
Original Postscript figures(240kB), (240kB).
).
Original Postscript figures(240kB), (240kB).
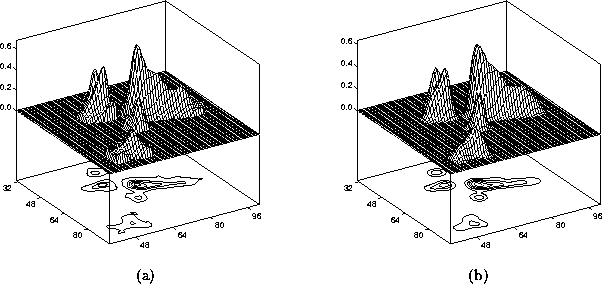
Figure:
Reconstruction via the GCE;
a: with a uniform prior 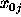 on the support provided by WIPE| (
on the support provided by WIPE| ( );
b: with a smoothed version of the previous prior (
);
b: with a smoothed version of the previous prior (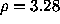 ).
Original Postscript figures(240kB), (240kB).
).
Original Postscript figures(240kB), (240kB).
References:
Lannes, A., Anterrieu, E., & Bouyoucef, K., 1994, J. Mod. Opt., 41, 1537
Lannes, A., Anterrieu, E., & Bouyoucef, K., 1996, J. Mod. Opt., 43, 105
Lannes, A., Anterrieu, E., & Maréchal, P., 1997, A&AS, in
press
Maréchal, P., & Lannes, A. 1996, Inverse Problems, 12, 1
© Copyright 1997
Astronomical Society of the Pacific,
390 Ashton Avenue, San Francisco, California 94112, USA
Next: Determination of Variable Time Delay in Uneven Data Sets
Previous: A Computer-Based Technique for Automatic Description and
Classification of Newly-Observed Data
Up: Algorithms
Table of Contents - Index - PS reprint - PDF reprint
payne@stsci.edu
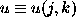 denote the spatial frequency
corresponding to the baseline
denote the spatial frequency
corresponding to the baseline 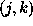 of the
interferometric device, and let
of the
interferometric device, and let 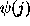 be the aberration phase
term of pupil element j .
The central problem is to reconstruct both the brightness distribution
be the aberration phase
term of pupil element j .
The central problem is to reconstruct both the brightness distribution 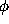 (of some object) and the pupil phase function
(of some object) and the pupil phase function 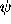 , by using as data
complex-visibility measurements of the form
, by using as data
complex-visibility measurements of the form 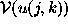 .
The latter are related to
.
The latter are related to 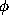 and
and 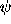 by the equation
by the equation
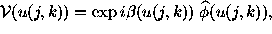 in which
in which 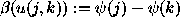 and
and 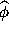 is the Fourier transform of
is the Fourier transform of 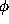 . Solving for
. Solving for 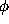 (assuming that
(assuming that 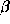 is known) is a Fourier synthesis operation, while solving for
is known) is a Fourier synthesis operation, while solving for 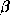 corresponds to a phase calibration operation. The whole problem
must be solved in such a way that the solution is not too sensitive to
unavoidable measurement errors. In other words, the inverse problem
under consideration must be regularized, and it is essential that the chosen
methodology provides an estimation of the reconstruction stability. In fact, the Fourier
synthesis operation proves to be the core of the problem. It has the form
of a linear inverse problem. The corresponding ``measurement equation''
may be written as
y = A x,
in which
corresponds to a phase calibration operation. The whole problem
must be solved in such a way that the solution is not too sensitive to
unavoidable measurement errors. In other words, the inverse problem
under consideration must be regularized, and it is essential that the chosen
methodology provides an estimation of the reconstruction stability. In fact, the Fourier
synthesis operation proves to be the core of the problem. It has the form
of a linear inverse problem. The corresponding ``measurement equation''
may be written as
y = A x,
in which 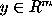 is the real-valued data vector associated with
is the real-valued data vector associated with
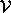 , A is the Fourier sampling operator, and x is the
vector formed with the components of
, A is the Fourier sampling operator, and x is the
vector formed with the components of 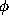 in an adequate basis
(Maréchal & Lannes 1996).
in an adequate basis
(Maréchal & Lannes 1996).
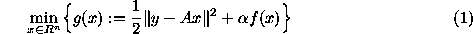
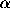 is the so-called regularization parameter. The
quadratic term in (1) forces the object to fit the data, while
the regularization term stabilizes the solution with respect to
small variations in y (and of course ensures uniqueness).
Denoting by
is the so-called regularization parameter. The
quadratic term in (1) forces the object to fit the data, while
the regularization term stabilizes the solution with respect to
small variations in y (and of course ensures uniqueness).
Denoting by 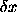 the variation of the solution
the variation of the solution 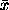 induced by a variation
induced by a variation 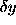 , the stability is
governed by an inequality such as
, the stability is
governed by an inequality such as

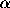 .
We emphasize that the regularization term should also
be designed so that g has a physical meaning, so that
the solution
.
We emphasize that the regularization term should also
be designed so that g has a physical meaning, so that
the solution 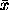 can be easily interpreted.
can be easily interpreted.
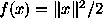 .
It can be generalized by choosing
.
It can be generalized by choosing
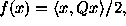 in which Q is a symmetric non-negative n × n matrix.
When x can be interpreted as a (discrete) probability density,
one often takes the Shannon entropy
in which Q is a symmetric non-negative n × n matrix.
When x can be interpreted as a (discrete) probability density,
one often takes the Shannon entropy 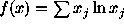 or
the Kullback measure
or
the Kullback measure
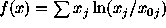 ,
in which
,
in which
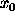 represents a prior knowledge of the object. If x is
only assumed to be positive, one can use the Generalized
Cross-Entropy (GCE)
represents a prior knowledge of the object. If x is
only assumed to be positive, one can use the Generalized
Cross-Entropy (GCE)
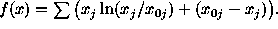 Let us also mention the Itakura-Saito criterion
Let us also mention the Itakura-Saito criterion
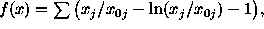 frequently used in spectral analysis.
frequently used in spectral analysis.
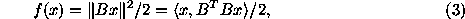
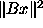 represents the energy of x
in the high frequency band (Lannes,
Anterrieu, & Bouyoucef 1994).
Clearly, this regularization principle belongs to the Tikhonov family, since
represents the energy of x
in the high frequency band (Lannes,
Anterrieu, & Bouyoucef 1994).
Clearly, this regularization principle belongs to the Tikhonov family, since
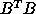 is a symmetric non-negative n × n matrix. It is very
closely related to the notion of resolution. The function to be minimized in (1)
takes the form
is a symmetric non-negative n × n matrix. It is very
closely related to the notion of resolution. The function to be minimized in (1)
takes the form 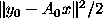 with
with 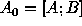 and
and 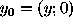 .
This kind of function is efficiently minimized by a conjugate-gradients
algorithm, which has the advantage of providing (with negligible
additional computing time) an estimate of the condition number and, thereby,
control of the stability of the reconstruction process.
As for the matching pursuit strategy, we simply mention that the
main difference from ÇLEAN| is that it can be conducted
at the level of the scaling functions of the object workspace (Lannes,
Anterrieu, & Bouyoucef 1994)
.
This kind of function is efficiently minimized by a conjugate-gradients
algorithm, which has the advantage of providing (with negligible
additional computing time) an estimate of the condition number and, thereby,
control of the stability of the reconstruction process.
As for the matching pursuit strategy, we simply mention that the
main difference from ÇLEAN| is that it can be conducted
at the level of the scaling functions of the object workspace (Lannes,
Anterrieu, & Bouyoucef 1994)
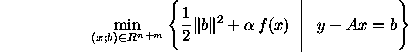
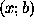 is a random vector
to which a prior probability measure
is a random vector
to which a prior probability measure 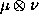 is assigned.
The Maximum Entropy Principle is then used to infer a posterior
probability on
is assigned.
The Maximum Entropy Principle is then used to infer a posterior
probability on 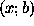 , and finally, we choose the expectancy
of x under the inferred density
, and finally, we choose the expectancy
of x under the inferred density 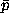 as the solution
to our inverse problem. The core of the PMEM is an
infinite dimensional linearly constrained optimization problem
(Maréchal & Lannes 1996)
in which the functional to be minimized is (the continuous version of)
the Kullback information measure. As explicitly
shown in Maréchal & Lannes (1996), it can be solved by means of a dual strategy. It is then possible
to demonstrate that, for particular choices of the priors
as the solution
to our inverse problem. The core of the PMEM is an
infinite dimensional linearly constrained optimization problem
(Maréchal & Lannes 1996)
in which the functional to be minimized is (the continuous version of)
the Kullback information measure. As explicitly
shown in Maréchal & Lannes (1996), it can be solved by means of a dual strategy. It is then possible
to demonstrate that, for particular choices of the priors 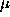 and
and  ,
the PMEM
gives rise to some of the most classical regularization techniques.
For example, a
Gaussian
,
the PMEM
gives rise to some of the most classical regularization techniques.
For example, a
Gaussian  with
with 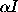 as the covariance matrix, associated with
a Gaussian
as the covariance matrix, associated with
a Gaussian 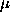 with covariance Q , gives rise to a Tikhonov regularization technique.
In particular,
if
with covariance Q , gives rise to a Tikhonov regularization technique.
In particular,
if 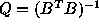 (provided that
(provided that 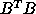 is positive definite),
we retrieve
WIPE|. Now, taking the multidimensional Poissonian distribution with vector
parameter
is positive definite),
we retrieve
WIPE|. Now, taking the multidimensional Poissonian distribution with vector
parameter 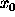 as
as 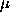 yields the GCE regularizer (Lannes,
Anterrieu, & Bouyoucef 1994),
and the Gamma law
with vector parameter
yields the GCE regularizer (Lannes,
Anterrieu, & Bouyoucef 1994),
and the Gamma law
with vector parameter 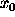 gives rise to the Itakura-Saito criterion.
Note that in this description, the quadratic fit term derives
from the standard Gaussian
prior measure on b . If another kind of noise were to corrupt the data,
this prior may, of course, be replaced by the appropriate one.
gives rise to the Itakura-Saito criterion.
Note that in this description, the quadratic fit term derives
from the standard Gaussian
prior measure on b . If another kind of noise were to corrupt the data,
this prior may, of course, be replaced by the appropriate one.
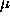 )
must be governed
by the nature of the imaging operator A . The next paragraph illustrates the
importance of this point.
)
must be governed
by the nature of the imaging operator A . The next paragraph illustrates the
importance of this point.
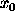 is a smoothed (and normalized) version of the
characteristic function of the previous support (Figure 2(b)). For the Shannon entropy
and the GCE, the regularization parameter
is a smoothed (and normalized) version of the
characteristic function of the previous support (Figure 2(b)). For the Shannon entropy
and the GCE, the regularization parameter 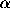 was adjusted in such a way that the final
fit term is equal to that reached by WIPE|.
The best reconstructed images, shown in Figures 1(b) and 2(b), are quite similar,
the values of the stability parameter
was adjusted in such a way that the final
fit term is equal to that reached by WIPE|.
The best reconstructed images, shown in Figures 1(b) and 2(b), are quite similar,
the values of the stability parameter 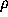 being reasonably small. In both cases,
the inverse problem is well regularized.
However, for the selected resolution,
the best stability is obtained with the WIPE| regularizer.
being reasonably small. In both cases,
the inverse problem is well regularized.
However, for the selected resolution,
the best stability is obtained with the WIPE| regularizer.

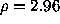 ).
Original Postscript figures
).
Original Postscript figures
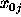 on the support provided by WIPE| (
on the support provided by WIPE| (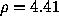 );
b: with a smoothed version of the previous prior (
);
b: with a smoothed version of the previous prior (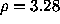 ).
Original Postscript figures
).
Original Postscript figures