



 1088 kB PostScript reprint
1088 kB PostScript reprint
Next: Cheating Poisson: A
Up: Statistical Analysis
Previous: Spatial Models and
Astronomical Data Analysis Software and Systems IV
ASP Conference Series, Vol. 77, 1995
Book Editors: R. A. Shaw, H. E. Payne, and J. J. E. Hayes
Electronic Editor: H. E. Payne
L. Pásztor
MTA TAKI, H-1022 Budapest, Herman Ottó út 15,
Hungary
C. Gallart, A. Aparicio, J. M. Vílchez
IAC, Vía Láctea a/n 38200 La Laguna, Tenerife,
Spain
Abstract:
The spatial distribution of stars in the Local Group dwarf
irregular galaxy NGC 6822 has been studied, using recent
positions and deep photometry for about 15,000 stars in the
galaxy. Based on photometrical data, OB stars and red stars
could be studied separately. Spatial statistical tools have
been applied to the analysis of the spatial structure. The
primary aim of the analysis was to find associations among
OB stars of the sample in statistical way; that is to
quantify the grouping tendency visible in the images of the
dwarf galaxy with the aid of merely statistical models. In the
present paper the technical aspects of the analysis
are discussed.
The Local Group dwarf irregular galaxy NGC 6822 is
characterized by small dimensions and structural simplicity;
its distance is about 500 kpc. The surface distribution of stars
in the direction of NGC 6822 (total: 22,958 objects)
came from recent position and deep photometric
observations (Gallart et al. 1994 and references
therein). After removing the foreground contamination
(estimated by the aid of a representative comparison field
located near to the galaxy) 15,343 objects retained in the
sample.
Blue stars [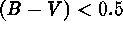 and
and 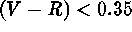 ; a total of 1,631
objects] and red stars [
; a total of 1,631
objects] and red stars [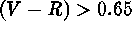 ; a total of 8,998 objects]
in the filtered sample were separated in
; a total of 8,998 objects]
in the filtered sample were separated in 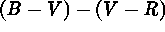 parameter space which was accompanied by a separation
also in 2D geometrical space (a similar effect was
published for NGC 3109 by Bresolin et al. 1993).
parameter space which was accompanied by a separation
also in 2D geometrical space (a similar effect was
published for NGC 3109 by Bresolin et al. 1993).
Our approach to group identification has been based on
merely statistical tools, as opposed to recent works on
similar efforts finding associations in nearby galaxies,
like Bresolin et al. (1993 or Wilson (1991, 1992). The main
characteristic of the present method is the subsequent
refinement of point process models fitted to the sample.
Rejection of CSR, (complete spatial randomness; for
details on the following spatial statistical models see
Pásztor and Tóth 1995) was based on the results
of the NNS (nearest-neighbors statistic). Principles of NNS
can be summarized as follows. Consider every pair of
objects whose separation is less than a predefined limit:
The number of pairs whose distance is between 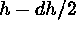 and
and
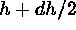 versus their separation is a well defined
function, and widely used in point pattern analysis. This function is
the derivative of another important point process
function, the K function which is related to
second-order properties of point processes (for details see
Cressie 1991). For HPP (homogeneous Poisson point process),
the function is linear: upward deviation indicates aggregation,
while a deviation downward is due to some regularity in the point pattern.
The significance of deviation from CSR results from
comparisons to 100 Monte Carlo simulations of HPP, so the significance of
deviation from CSR is
versus their separation is a well defined
function, and widely used in point pattern analysis. This function is
the derivative of another important point process
function, the K function which is related to
second-order properties of point processes (for details see
Cressie 1991). For HPP (homogeneous Poisson point process),
the function is linear: upward deviation indicates aggregation,
while a deviation downward is due to some regularity in the point pattern.
The significance of deviation from CSR results from
comparisons to 100 Monte Carlo simulations of HPP, so the significance of
deviation from CSR is 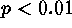 for every scale.
for every scale.
Refinement of the model was carried out by taking into
consideration the apparent large-scale structure present in
the sample. The newer 100 Monte Carlo simulations were generated as
realizations of IPP (inhomogeneous Poisson point process)
with fixed (and identical with that of the real sample)
marginal distributions (Pásztor et al. 1993). Result of
NNS (Figure.1) shows significant (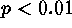 ) clustering at
around the scales of 25, 40, 65, and 90pc, and additionally
vacancies at scales smaller than 5pc. This latter is
a resukt of an SIP (simple inhibition point process),
and is probably due to the limit in resolution of the
observations.
) clustering at
around the scales of 25, 40, 65, and 90pc, and additionally
vacancies at scales smaller than 5pc. This latter is
a resukt of an SIP (simple inhibition point process),
and is probably due to the limit in resolution of the
observations.
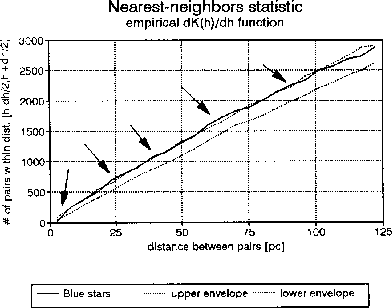
Figure: Identification of significant scales by NNS.
Original PostScript figure (249 kB)
All of the objects which dominant the
significant clustering at a given scale are thought to be
members of groups with a characteristic size comparable with
the scale value. However the number, shape, and location of
these groups is a priori unknown. A sequence of
non-hierarchical clustering models was carried out, providing partitions
of the sample as well as results of PCP (Poisson
cluster process) models. In choosing an optimum and
minimal model over the set of these competing models, an
information theoretic criterion, the CAIC (a more
strictly inforced version of Akaike's Information
Criterion) (Eisenblätter and Bozdogan 1988), was used
(Figure 2).
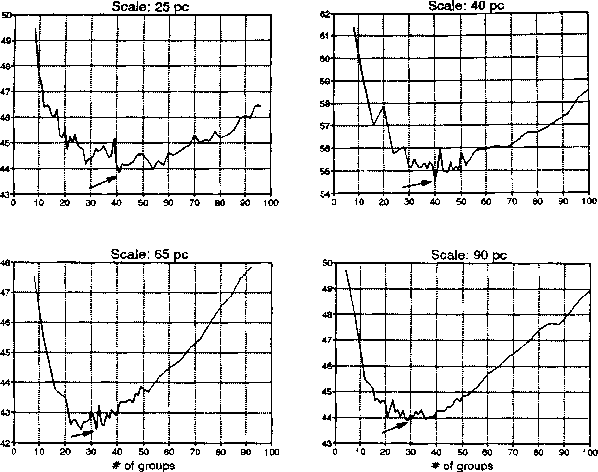
Figure: Model selection by the aid of CAIC.
Original PostScript figure (413 kB)
A final partition of the blue stars into groups (associations)
on the level characterized by characteristics scale of 25,
40, 65, and 90pc can be seen on Figure 3. Circles with
radii of the scale values should not be interpreted as anything but models
of fuzzy sets with radii varying around these values.
Th centers scattered around the centers of the resultant
circles, and shapes are approximate.

Figure: Clustering of OB stars on scales of 25, 40, 65 and 90 pc.
Original PostScript figure (370 kB)
Acknowledgments:
L. Pásztor was partially supported by the Hungarian State
Research Found (Grant No. OTKA-F 4239). L. Pásztor is
grateful to the Organizers of the conference and the Hungarian
State Research Found for the travel grants.
References:
Bresolin, F., Capaccioli, M., & Piotti, G. 1993, AJ, 105, 1779
Cressie, N. A. C. 1991, Statistics for Spatial Data
(New York, Wiley)
Eisenblätter, D., & Bozdogan, H. 1988, in Classification and
Related Methods of Data Analysis, ed. H. H. Bock (Amsterdam,
North-Holland), p. 91
Gallart, C., Aparacio, A., Chiosi, C., Bertelli, G., &
Vílchez, J. M. 1994, ApJ, 425, L9
Pásztor, L., Tóth, L. V., & Balázs, L. G. 1993, A&A, 268, 108
Pásztor, L., Tóth, L. V. 1995, 
Wilson, C. D. 1991, AJ, 101, 1663
Wilson, C. D. 1992, ApJ, 384, L29




 1088 kB PostScript reprint
1088 kB PostScript reprint
Next: Cheating Poisson: A
Up: Statistical Analysis
Previous: Spatial Models and
adass4_editors@stsci.edu
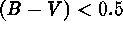 and
and 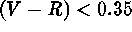 ; a total of 1,631
objects] and red stars [
; a total of 1,631
objects] and red stars [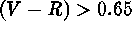 ; a total of 8,998 objects]
in the filtered sample were separated in
; a total of 8,998 objects]
in the filtered sample were separated in 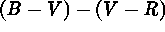 parameter space which was accompanied by a separation
also in 2D geometrical space (a similar effect was
published for NGC 3109 by Bresolin et al. 1993).
parameter space which was accompanied by a separation
also in 2D geometrical space (a similar effect was
published for NGC 3109 by Bresolin et al. 1993).
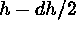 and
and
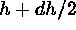 versus their separation is a well defined
function, and widely used in point pattern analysis. This function is
the derivative of another important point process
function, the K function which is related to
second-order properties of point processes (for details see
Cressie 1991). For HPP (homogeneous Poisson point process),
the function is linear: upward deviation indicates aggregation,
while a deviation downward is due to some regularity in the point pattern.
The significance of deviation from CSR results from
comparisons to 100 Monte Carlo simulations of HPP, so the significance of
deviation from CSR is
versus their separation is a well defined
function, and widely used in point pattern analysis. This function is
the derivative of another important point process
function, the K function which is related to
second-order properties of point processes (for details see
Cressie 1991). For HPP (homogeneous Poisson point process),
the function is linear: upward deviation indicates aggregation,
while a deviation downward is due to some regularity in the point pattern.
The significance of deviation from CSR results from
comparisons to 100 Monte Carlo simulations of HPP, so the significance of
deviation from CSR is 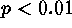 for every scale.
for every scale.
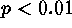 ) clustering at
around the scales of 25, 40, 65, and 90pc, and additionally
vacancies at scales smaller than 5pc. This latter is
a resukt of an SIP (simple inhibition point process),
and is probably due to the limit in resolution of the
observations.
) clustering at
around the scales of 25, 40, 65, and 90pc, and additionally
vacancies at scales smaller than 5pc. This latter is
a resukt of an SIP (simple inhibition point process),
and is probably due to the limit in resolution of the
observations.


