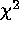 score or number of standard deviations,
but for this purpose it is more convenient to work with
raw probabilities.) A uniform threshold is applied to
the significance list to determine which detections are to be included
in the catalog.
score or number of standard deviations,
but for this purpose it is more convenient to work with
raw probabilities.) A uniform threshold is applied to
the significance list to determine which detections are to be included
in the catalog.
J. W. Lewis
Center for EUV Astrophysics, 2150 Kittredge St., University
of California, Berkeley, CA 94720--5030
This result does not, however, imply that real sources below the limiting catalog threshold cannot be reliably detected. If one has some prior knowledge of where the real sources are likely to be found, it is possible to ``cheat Poisson'' and include these sub-threshold sources without introducing significant numbers of spurious detections. This paper describes the theoretical and practical aspects of the biased search technique as applied to EUVE all-sky survey skymaps.
Consider the problem of producing a catalog of point sources from a data set dominated by background noise where many sources will have low signal-to-noise ratios. The goal is to include as many sources as possible without introducing a large number of spurious detections. It may be the case that a threshold strict enough to reduce the spurious detections to an acceptable number may exclude large numbers of faint, yet interesting sources. This loss is the unfortunate price one must pay to produce an unbiased catalog.
In some situations, however, certain types of bias may be acceptable. For example, the Extreme Ultraviolet Explorer ( EUVE) has conducted an all-sky survey and is now being used to obtain deep, pointed exposures of interesting targets. A guest observer interested in a specific, perhaps rare, class of objects may wish to use the survey data to determine which objects of that class might be good candidates for pointed observations, even if the potential targets were too faint to be included in an unbiased survey catalog. The prior information that an object of the correct type is known to exist near the position of a marginal detection can increase our confidence that the detection is not spurious, and that scheduling an observation of that target will not be a waste of precious instrument time.
In the unbiased approach, we apply the detection algorithm of choice
to compute the significance at each point on the sky. Every significance
value corresponds to a probability that the detection is a false alarm
caused by random background variations. (The significance is usually
expressed as a 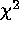 score or number of standard deviations,
but for this purpose it is more convenient to work with
raw probabilities.) A uniform threshold is applied to
the significance list to determine which detections are to be included
in the catalog.
score or number of standard deviations,
but for this purpose it is more convenient to work with
raw probabilities.) A uniform threshold is applied to
the significance list to determine which detections are to be included
in the catalog.
The number of spurious detections in the catalog will be a random variable,
approximating a Poisson distribution with expectation 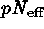 ,
where p is the threshold false alarm probability, and
,
where p is the threshold false alarm probability, and 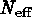 is the effective number of independent trials.
The value of
is the effective number of independent trials.
The value of 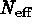 will depend strongly on the size and shape of
the instrument point-spread function (PSF), the pixel size (for binned data),
and the amount of sky covered by the survey. A crude estimate of
will depend strongly on the size and shape of
the instrument point-spread function (PSF), the pixel size (for binned data),
and the amount of sky covered by the survey. A crude estimate of
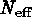 is given by
is given by

where 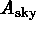 is the sky area surveyed, and
is the sky area surveyed, and 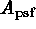 is some
measure of the PSF area; but this estimate is highly dependent on the shape
of the PSF. (Consider two points separated by less than one PSF diameter;
their significance will be somewhat correlated because of overlapping PSFs,
but the amount of correlation will depend on how peaked the PSF is.)
is some
measure of the PSF area; but this estimate is highly dependent on the shape
of the PSF. (Consider two points separated by less than one PSF diameter;
their significance will be somewhat correlated because of overlapping PSFs,
but the amount of correlation will depend on how peaked the PSF is.)
It may be easier to estimate 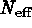 empirically via Monte Carlo
methods, e.g., generating a random, background-only data set and applying
the detection algorithm to assess the false alarm rate (Lewis 1993).
Simulation results indicate that
empirically via Monte Carlo
methods, e.g., generating a random, background-only data set and applying
the detection algorithm to assess the false alarm rate (Lewis 1993).
Simulation results indicate that 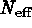 is approximately
is approximately 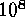 for the shortest wavelength EUVE survey coverage and PSF. Regardless
of the PSF shape,
for the shortest wavelength EUVE survey coverage and PSF. Regardless
of the PSF shape, 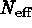 will generally be proportional to the area
of sky surveyed.
will generally be proportional to the area
of sky surveyed.
The disadvantage of the unbiased approach is that for large sky coverage
and small PSF area, one must use a rather strict detection threshold to
prevent catalog contamination from excessive numbers of spurious detections.
For the first EUVE catalog (Bowyer et al. 1994), the detection
thresholds were in the neighborhood from approximately 5.5  to
6
to
6 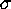 , which excluded many interesting sources.
, which excluded many interesting sources.
Suppose the source search were restricted to those areas immediately
surrounding a small (relative to 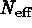 for an all-sky unbiased survey)
set of objects that we expect, a priori, to detect in the all-sky data.
If the search radius around each catalog location is on the order of
one PSF radius, the effective number of trials will be close to the
size of the input catalog (assuming the points are well separated).
This constraint can reduce
for an all-sky unbiased survey)
set of objects that we expect, a priori, to detect in the all-sky data.
If the search radius around each catalog location is on the order of
one PSF radius, the effective number of trials will be close to the
size of the input catalog (assuming the points are well separated).
This constraint can reduce 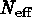 by several orders of magnitude, allowing a corresponding relaxation in the threshold probability to achieve
the same expected number of spurious detections. By using an input catalog
of a few thousand objects, detection thresholds from approximately 3
by several orders of magnitude, allowing a corresponding relaxation in the threshold probability to achieve
the same expected number of spurious detections. By using an input catalog
of a few thousand objects, detection thresholds from approximately 3 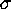 to 4
to 4 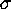 become feasible, allowing a substantial increase in the number
of objects detected without a severe penalty in spurious detections.
become feasible, allowing a substantial increase in the number
of objects detected without a severe penalty in spurious detections.
The biased catalog search suffers from the obvious problem of inheriting all biases present in the input catalog and will never result in unexpected detections (which are, in a sense, the most interesting kind). We can combine the best features of both approaches by using the following hybrid approach.
As in the unbiased case, we apply the detection algorithm to the all-sky
data set and apply a strict, uniform significance threshold, 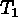 . Instead
of immediately discarding detections failing the significance test, we
apply a second, more liberal threshold,
. Instead
of immediately discarding detections failing the significance test, we
apply a second, more liberal threshold, 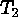 , to the leftover detections.
Any of these marginal detections corresponding to previously cataloged
objects are added to the final catalog.
, to the leftover detections.
Any of these marginal detections corresponding to previously cataloged
objects are added to the final catalog.
The existence of a cataloged object near a marginal detection
is prior information that effectively increases our confidence
that the detection is not spurious. The significance boost can be
expressed in terms of the input catalog size and the positional
tolerance in the matching process. We assume that the input catalog
sources are in an approximately uniform distribution over the entire sky,
and that they are almost always separated by at least one search radius.
If 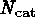 is the size of the input catalog, and
is the size of the input catalog, and 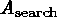 is the area within one search radius of a detection, the probability q that
a random point on the sky will be within one search radius of a cataloged
object is given by
is the area within one search radius of a detection, the probability q that
a random point on the sky will be within one search radius of a cataloged
object is given by

We presume the existence of a detection at a given point with false alarm
probability p, and the existence of a cataloged object near that point
with coincidence probability q, are independent events. Therefore the
joint false alarm probability 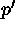 is simply
is simply

Since 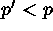 , we have lowered the false alarm probability by
finding a nearby cataloged object. It is obviously advantageous to have
q as small as possible. Any objects in the input catalog unlikely to be
detected in the survey data should be pruned to reduce the number of
potential coincidences. For example, we used several on-line catalogs such
as SIMBAD and NED in an attempt to identify newly detected EUVE
sources. Many of our on-line catalog ``hits'' turned out to be IRAS
sources and faint galaxies in directions of high hydrogen column density
(Bowyer et al. 1994) and, therefore, highly unlikely to be detected in the
extreme ultraviolet (EUV) bandpasses. After pruning these implausible
objects, we observed a coincidence rate q of about 0.03 in a
sample of 100 random points using a search radius of 3 arcmin.
, we have lowered the false alarm probability by
finding a nearby cataloged object. It is obviously advantageous to have
q as small as possible. Any objects in the input catalog unlikely to be
detected in the survey data should be pruned to reduce the number of
potential coincidences. For example, we used several on-line catalogs such
as SIMBAD and NED in an attempt to identify newly detected EUVE
sources. Many of our on-line catalog ``hits'' turned out to be IRAS
sources and faint galaxies in directions of high hydrogen column density
(Bowyer et al. 1994) and, therefore, highly unlikely to be detected in the
extreme ultraviolet (EUV) bandpasses. After pruning these implausible
objects, we observed a coincidence rate q of about 0.03 in a
sample of 100 random points using a search radius of 3 arcmin.
The expected number of spurious detections in the biased component of the
hybrid catalog is qM, where M is the count of marginal
detections between the two thresholds 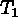 and
and 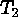 .
.
Detection and Flux Service
Researchers interested in applying these concepts to EUVE all-sky survey data are invited to use CEA's in-house software via our on-line source detection server. This service allows the user to supply a list of coordinates and receive a list of detection significance, flux, best-fit position, and other relevant data by e-mail, usually within a few hours of submitting the request. A skymap image server is also available to allow users to obtain images of skymap regions of interest. A great deal of general EUVE sky survey documentation is also available to assist users in interpreting the results.
When dealing with marginal detections, it is important to keep in mind that the discussion in this paper only addresses spurious detections arising from random background fluctuations. A possibility always exists that at very low significance thresholds, any detection algorithm may respond more to deviations from the underlying background model than to the putative source itself. We have found that analysis of large ensembles of randomly placed test points is a useful tool to assess the presence and severity of systematic deviations from any claimed statistical properties of the significance reported by the detection software. In some cases, it may be advisable to use perturbed versions of the input catalog (e.g., adding 1^o of ecliptic latitude to each object's coordinates) if one suspects spurious detections are correlated with known problematic skymap features. Finally, it is always a good idea to visually inspect the skymap at each claimed detection to rule out significance errors from diffuse skymap features, exposure edges, or strong background gradients.
We thank the principal investigator, Stuart Bowyer, and the EUVE science team for their advice and support. This research has been supported by NASA contract NAS5--30180.
Lewis, J. 1993, Journal of the British Interplanetary Society, 46, 346