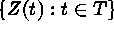 ; where
; where 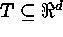 . Here T
is the index set,
. Here T
is the index set, 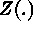 is the spatial process,
is the spatial process, 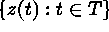 is a realization of the process. In the present
paper we give a brief overview on the most important spatial
statistical models,
is a realization of the process. In the present
paper we give a brief overview on the most important spatial
statistical models,
L. Pásztor
MTA TAKI, H-1022 Budapest Herman Ottó út 15,
Hungary
L. V. Tóth
Dept. of Astr., Eötvös Univ., H-1083 Budapest
Ludovika tér 2, Hungary
Consider 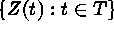 ; where
; where 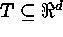 . Here T
is the index set,
. Here T
is the index set, 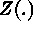 is the spatial process,
is the spatial process, 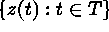 is a realization of the process. In the present
paper we give a brief overview on the most important spatial
statistical models,
is a realization of the process. In the present
paper we give a brief overview on the most important spatial
statistical models,
to illustrate the range of problems that can be addressed and the wide applicability of spatial statistical models in astronomy.
A usual spatial point process is defined as 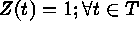 (i.e., the index set is the points of
(i.e., the index set is the points of
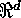 ) or
) or 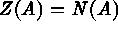 [the number of points within A];
[the number of points within A]; 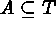 (i.e., the index set is the units of
(i.e., the index set is the units of 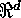 ),
where both
),
where both 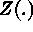 and T are random. First- and second-order
properties of a spatial point process are the
intensity function:
and T are random. First- and second-order
properties of a spatial point process are the
intensity function: 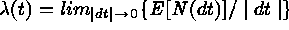 ; and the second-order intensity
function:
; and the second-order intensity
function: 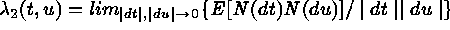 . Spatial point processes are the mathematical
models producing point patterns as their realization.
. Spatial point processes are the mathematical
models producing point patterns as their realization.
A number of processes are available for modeling the patterns that arise in nature:
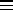 homogeneous
Poisson process (HPP). The number of points for
homogeneous
Poisson process (HPP). The number of points for 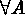 has a Poisson distribution with mean
has a Poisson distribution with mean 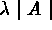 ;
counts in disjoint sets are independent.
;
counts in disjoint sets are independent.
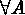 has a Poisson
distribution with mean
has a Poisson
distribution with mean 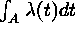 . Counts in
disjoint sets are independent. For a Cox process
(CP; doubly stochastic point process)
. Counts in
disjoint sets are independent. For a Cox process
(CP; doubly stochastic point process) 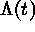 is a
non-negative valued stochastic process. Conditional on
is a
non-negative valued stochastic process. Conditional on
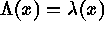 , the events form an IPP with
intensity function
, the events form an IPP with
intensity function 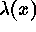 . For a Poisson cluster
process (PCP; Neyman-Scott process) parent
events form an IPP. Each parent produces a random number
of offspring, realized independently
according to a discrete probability
distribution. The position of the offspring relative to
their parents are independently distributed
according to a d-dimensional density function. The final
process is composed of the superposition of offspring only.
Multi-generation process is the generalization of
PCP, where offspring are parents of the next generation.
. For a Poisson cluster
process (PCP; Neyman-Scott process) parent
events form an IPP. Each parent produces a random number
of offspring, realized independently
according to a discrete probability
distribution. The position of the offspring relative to
their parents are independently distributed
according to a d-dimensional density function. The final
process is composed of the superposition of offspring only.
Multi-generation process is the generalization of
PCP, where offspring are parents of the next generation.
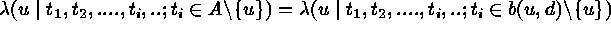 ,
where
,
where 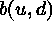 is the closed ball of radius d centered at
u (Strauss process, Pair-potential Markov point
process, Gibbs process ).
is the closed ball of radius d centered at
u (Strauss process, Pair-potential Markov point
process, Gibbs process ).
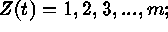
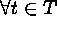 (i.e., the index set
is the points of
(i.e., the index set
is the points of 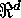 ) or
) or 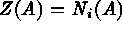 [number of i
points within A];
[number of i
points within A]; 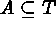 (i.e., the index set is
the units of
(i.e., the index set is
the units of 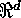 ), where both
), where both 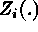 and T are
random. The m univariate spatial point processes are the
components of the multivariate process, which is thus
characterized by m intensity functions and
and T are
random. The m univariate spatial point processes are the
components of the multivariate process, which is thus
characterized by m intensity functions and 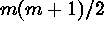 second-order intensity functions. The terminology reflects the
components of the process (e.g., bivariate Cox process).
second-order intensity functions. The terminology reflects the
components of the process (e.g., bivariate Cox process).
Examples of applicability in astronomy include: (1) revealing regularity in the spatial distribution of point-like objects, (2) identification of important scales in the spatial distribution of point-like objects, (3) stellar statistics (deriving distributions, testing of predicted distribution functions, identification of clusters and associations of stars, search for wide binaries and multiple systems), and (4) cosmological problems (testing of predicted distribution functions, identification of galaxy clusters, voids, etc.).
The spatial index t varies continuously throughout a fixed
subset T of a d-dimensional Euclidean space. Term
``regionalized'' was introduced in order to emphasize the
continuous spatial nature of the index set T. The prefix
``geo'' reflects the fact that the theory's roots are in
geographical and geological applications. Random processes
are usually characterized by their moment measures. In
geostatistics, ``semivariogram'' plays a crucial role. If
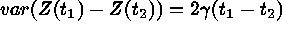 for
for 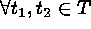 ;
; 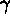 is called semivariogram. If
is called semivariogram. If
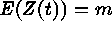 for
for 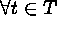 and
and 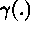 exist,
exist,
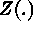 is intrinsically stationary. Semivariogram is
conditional negative-definite. If
is intrinsically stationary. Semivariogram is
conditional negative-definite. If 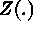 is second-order
stationary
is second-order
stationary 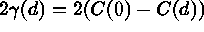 . Linear, spherical,
and exponential models are simple isotropic (semi)variogram.
. Linear, spherical,
and exponential models are simple isotropic (semi)variogram.
The most important application of the (semi)variogram is
``kriging,'' a stochastic spatial interpolation method
which depends on the second-order properties of the process.
The principal aim of kriging is to provide accurate spatial
predictions from observed data. Kriging techniques are all
related and refined versions of the weighted moving average
originally used by Krige (1951) and based on the simple
linear model: 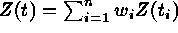 , where
, where  . Kriging provides optimum prediction in a
sense of minimizing mean-squared prediction error,
and also
. Kriging provides optimum prediction in a
sense of minimizing mean-squared prediction error,
and also
provides the estimation.
A useful decomposition is
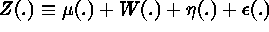 , where
, where 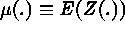 is the large-scale variation,
is the large-scale variation, 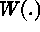 is
the smooth small-scale variation,
is
the smooth small-scale variation, 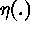 is the micro-scale variation,
is the micro-scale variation,
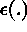 is the measurement error.
These models are widely applied in geosciences.
is the measurement error.
These models are widely applied in geosciences.
A number of astronomical applications of the method come to mind: (1) the creation of contour and/or surface maps in the case of incompletely sampled maps in extended radio surveys, (2) testing for completeness in sampling (whether the expected structure is revealed as spiral or filamentary), (3) testing whether resolution is achieved (in the cores of galaxies), (4) the creation of maps with resolution higher than the physical resolution of the observation (interpolations arising from the co-addition of separate sky coverage by IRAS or ISO), and (5) interpolations to reach a higher virtual resolution for comparisons (e.g., IRAS 12 and 100micron images).
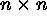 matrix,
matrix, 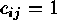 if sites i and j are juxtaposed,
if sites i and j are juxtaposed,
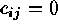 if not; n is the number of sites) or by a
graph-theoretic formalism (the sites become vertices, which
are connected with edges for contiguous objects). Examples
for realizations of lattice processes in 2-D are spot maps,
mosaics, and digital images. The most important application of
lattice models is statistical modeling of spatial images,
which is widespread in astronomical image processing
(restoration, segmentation, classification, reconstruction, etc.).
if not; n is the number of sites) or by a
graph-theoretic formalism (the sites become vertices, which
are connected with edges for contiguous objects). Examples
for realizations of lattice processes in 2-D are spot maps,
mosaics, and digital images. The most important application of
lattice models is statistical modeling of spatial images,
which is widespread in astronomical image processing
(restoration, segmentation, classification, reconstruction, etc.).
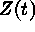 is
multidimensional. An example of multivariate
spatial statistics is provided by multiband image
processing. A generalization of the univariate
spatial statistical methods is provided by cokriging, where
spatial prediction of a variable is carried out with the aid
of another.
is
multidimensional. An example of multivariate
spatial statistics is provided by multiband image
processing. A generalization of the univariate
spatial statistical methods is provided by cokriging, where
spatial prediction of a variable is carried out with the aid
of another.
Examples of applicability to astronomy include: (1) 2-D classification of objects by their shape on images (e.g., star, galaxy identification on CCD or photographic images), (2) cloud identification from coordinate-velocity ``data cubes'' (e.g., radio spectroscopic observations), and (3) any advanced image processing technique, like maximum entropy or deconvolution (e.g., maximum correlation method in ``HIRES'' IRAS data processing at IPAC).
This research was partially supported by the Hungarian State Research Found (Grant No. OTKA-F 4239). L. Pásztor is grateful to ADASS and the Hungarian State Research Found for the travel grants.
Bahcall, J. N., & Soneira, R. M. 1981, ApJ, 246, 122
Bahcall, J. N., Jones, B. F., & Ratnatunga, K. U. 1986, ApJ, 60,939
Bucciarelli, B., Lattanzi, M. G., & Taff, L. G. 1993, ApJS, 84, 91
Cliff, A. D., & Ord, J. K., 1973, Spatial Autocorrelation (London, Pion)
Cressie, N. A. C. 1991, Statistics for Spatial Data (New York, Wiley)
Diggle, P. J. 1983, Statistical Analysis of Spatial Point Patterns (London, Academic Press)
Getis, A., & Boots, B. 1978, Models of Spatial Processes (Cambridge, Cambridge University Press)
Huang, J. S., & Shieh, W. R. 1990, Pattern Recognition, 23, 147
Journel, A. G., & Huijbregts, Ch. J. 1978, Mining Geostatistics (London, Academic Press)
Matheron, G. 1965, La Theorie des Variables Regionalisées et ses Applications (Paris, Masson)
Molina, R., Olmo, A., Perea, J., & Ripley, B. D. 1992, AJ, 103, 666
Pásztor, L., Tóth, L. V., & Balázs, L. G. 1993, A&A, 268, 108
Pásztor, L. 1993, in Astronomical Data Analysis Software and Systems II, ASP Conf. Ser., Vol. 52, eds. R.J. Hanisch, R.J.V. Brissenden, & J. Barnes (San Francisco, ASP), p. 7
Pásztor, L. 1994, in Astronomical Data Analysis Software and Systems III, ASP Conf. Ser., Vol. 61, eds. D. R. Crabtree, R. J. Hanisch, & J. Barnes (San Francisco, ASP), p. 253