



 216 kB PostScript reprint
216 kB PostScript reprint
Next: A Method for
Up: Statistical Analysis
Previous: Cheating Poisson: A
Astronomical Data Analysis Software and Systems IV
ASP Conference Series, Vol. 77, 1995
Book Editors: R. A. Shaw, H. E. Payne, and J. J. E. Hayes
Electronic Editor: H. E. Payne
K. Kearns, F. Primini, and D. Alexander
Smithsonian Astrophysical Observatory,
60 Garden St.,
Cambridge, MA 02138
Abstract:
We present a modified 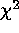 fitting technique,
useful for
fitting models to binned data with few counts per bin. We demonstrate
through numerical simulations that model parameters estimated with our
technique are essentially bias-free, even when the average number of
counts per bin is
fitting technique,
useful for
fitting models to binned data with few counts per bin. We demonstrate
through numerical simulations that model parameters estimated with our
technique are essentially bias-free, even when the average number of
counts per bin is 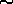 1. This is in contrast to the results from
traditional
1. This is in contrast to the results from
traditional 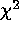 techniques, which exhibit significant biases in
such cases (see, for example, Nousek & Shue 1989; Cash 1979).
Moreover, our technique can explicitly handle bins with 0 counts,
obviating the need to ignore such bins or rebin the data. We conclude
with a discussion of the problem of estimating goodness-of-fit in the
limit of few counts using our modified
techniques, which exhibit significant biases in
such cases (see, for example, Nousek & Shue 1989; Cash 1979).
Moreover, our technique can explicitly handle bins with 0 counts,
obviating the need to ignore such bins or rebin the data. We conclude
with a discussion of the problem of estimating goodness-of-fit in the
limit of few counts using our modified 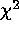 statistic.
statistic.
When fitting models to data with few counts, two of the most common
methods used are the standard 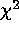 method and the C statistic. Use
of the
method and the C statistic. Use
of the 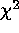 method requires that one avoid bins with 0 counts by
either ignoring them or rebinning, and produces significantly biased
results for data with few counts. The C-statistic gives unbiased results
but is difficult to interpret in terms of goodness-of-fit.
Neither approach is
ideal, though each is useful in some cases. The Iterative Weighting
Technique which we investigate here both addresses the
deficiencies inherent in using the standard method for data with few
counts, and provides a goodness-of-fit parameter which is
indistinguishable from the standard
method requires that one avoid bins with 0 counts by
either ignoring them or rebinning, and produces significantly biased
results for data with few counts. The C-statistic gives unbiased results
but is difficult to interpret in terms of goodness-of-fit.
Neither approach is
ideal, though each is useful in some cases. The Iterative Weighting
Technique which we investigate here both addresses the
deficiencies inherent in using the standard method for data with few
counts, and provides a goodness-of-fit parameter which is
indistinguishable from the standard 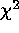 parameter for many datasets.
parameter for many datasets.
Iterative Weighting (IW) is an example of the class of weighted
least-squares estimators described by Wheaton et al. (1994), in
which 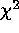 is expressed as a weighted sum of squared deviations,
is expressed as a weighted sum of squared deviations,
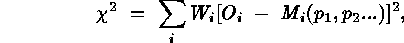
where 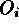 are the observed counts in bin i,
are the observed counts in bin i, 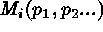 are
the counts predicted by the model M with parameters
are
the counts predicted by the model M with parameters 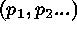 ,
and the weights
,
and the weights 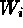 are the inverses of the true variances
are the inverses of the true variances
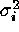 . As Wheaton et al. (1994) point out, the
approximation
. As Wheaton et al. (1994) point out, the
approximation 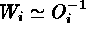 leads to significant biases in the
best-fit parameters, due to the strong anti-correlation between
leads to significant biases in the
best-fit parameters, due to the strong anti-correlation between 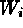 and
and 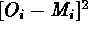 . Similar
biases are encountered if the approximation
. Similar
biases are encountered if the approximation 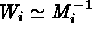 is
used (Nousek & Shue 1989).
The IW technique avoids such biases by estimating
is
used (Nousek & Shue 1989).
The IW technique avoids such biases by estimating 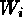 through
successive iterations, where for each iteration, j,
through
successive iterations, where for each iteration, j,
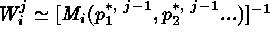 , and the best-fit
parameters
, and the best-fit
parameters 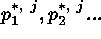 are determined by
minimization of
are determined by
minimization of
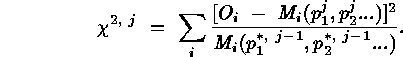
For the first iteration, all weights are set to 1.
In our sample, we find that the minimum 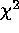 values
and
best-fit parameters converge after about 6 iterations.
values
and
best-fit parameters converge after about 6 iterations.
To demonstrate the IW technique, we repeat the simple numerical experiment
of Nousek & Shue (1989). For a
range of total counts, N, from 25 to 1000, we generate an ideal
power-law spectrum such that:
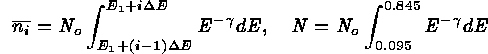
for 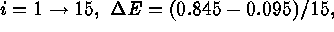 and
and 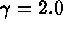 For each ideal spectrum, we simulate 1000 sample spectra {n
For each ideal spectrum, we simulate 1000 sample spectra {n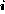 }, where
{n
}, where
{n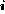 } are random deviates drawn from Poisson distributions with means
=
} are random deviates drawn from Poisson distributions with means
= 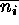 . We then determine best-fit model parameters
. We then determine best-fit model parameters
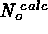 and
and
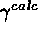 for each simulated spectrum, using IW
and Powell's method for function minimization (Press 1988). For
each N, we then compute
the average
for each simulated spectrum, using IW
and Powell's method for function minimization (Press 1988). For
each N, we then compute
the average 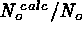 and
and 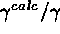 ; compile the
distributions of minimum
; compile the
distributions of minimum 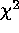 for comparison with the theoretical
distribution; and compute the percentage of simulations for which the
for comparison with the theoretical
distribution; and compute the percentage of simulations for which the
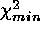 and
and 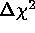 contours include
contours include 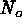 and
and 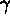 ,
for comparison with the expected percentages.
,
for comparison with the expected percentages.
In Table 
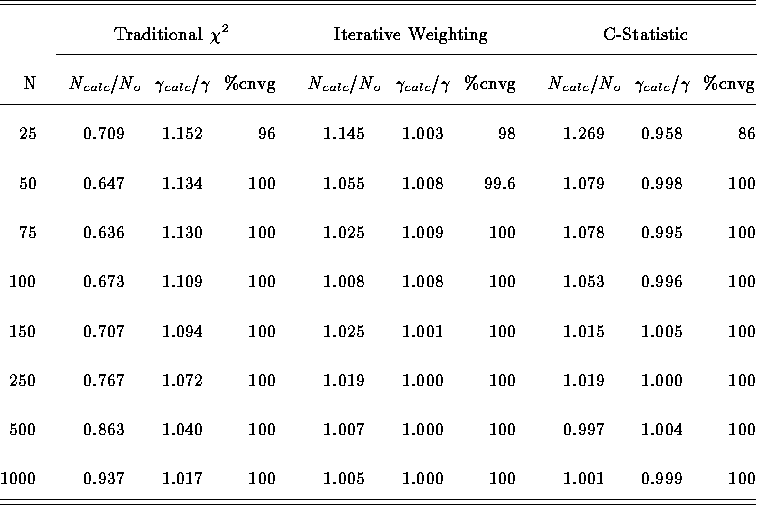
Table: Comparison of three fitting techniques.
we compare the biases (as measured by the ratios of average best-fit
parameter values to true values) in 1000 IW runs with those found for
traditional 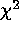 and the C statistic by Nousek & Shue in 250 runs.
We find that the IW biases are comparable to those encountered using
the C statistic for all N. These results are displayed in
Figure
and the C statistic by Nousek & Shue in 250 runs.
We find that the IW biases are comparable to those encountered using
the C statistic for all N. These results are displayed in
Figure  .
In Figure
.
In Figure  we compare both differential and cumulative
theoretical
we compare both differential and cumulative
theoretical 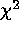 distributions with our observed
distributions. We apply a KS-test to the cumulative distributions and
find that at N=25 the match is poor, but by
N=100 the two distributions are in good agreement.
distributions with our observed
distributions. We apply a KS-test to the cumulative distributions and
find that at N=25 the match is poor, but by
N=100 the two distributions are in good agreement.
The percentage of simulations for which the
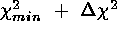 contours include
contours include 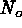 and
and 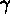 ,
for
,
for 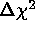 values appropriate to various joint two-parameter
confidence levels, is shown in
table
values appropriate to various joint two-parameter
confidence levels, is shown in
table  .
.
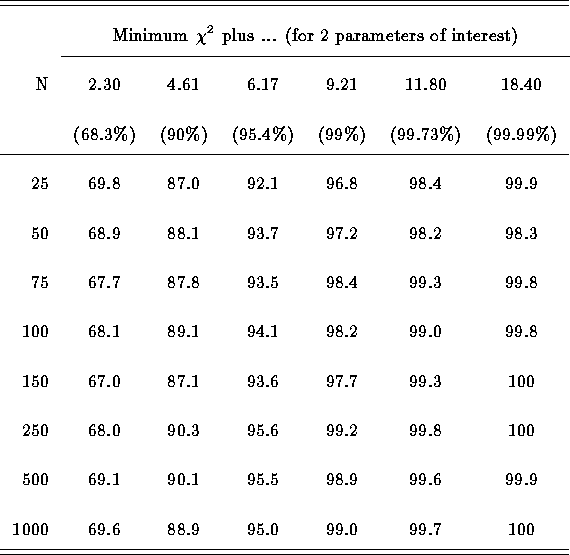
Table: Estimating Confidence Limits: Percentage of Best Fits Within Various
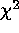 Boundaries, from a total of 1000 spectral fits.
Boundaries, from a total of 1000 spectral fits.
For most N, the measured and expected confidence levels are in good agreement.
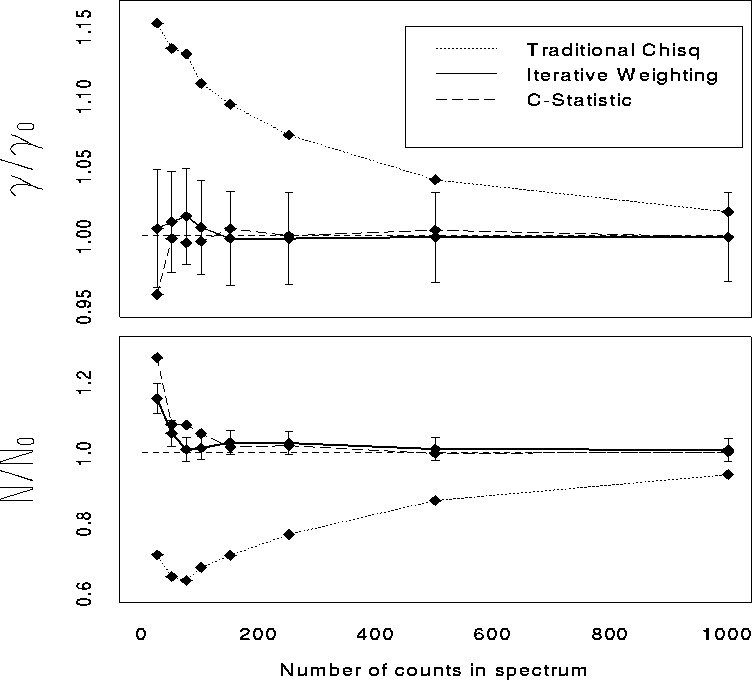
Figure: Bias in best-fit parameters for three fitting techniques.
Original PostScript figure (13 kB)
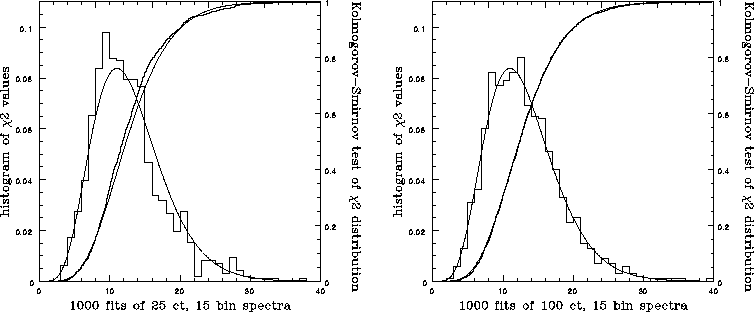
Figure: Comparison of theoretical 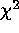 distribution with observed
distribution for IW by KS-test, with overlaid histograms.
Original PostScript figures
(56 kB),
(56 kB)
distribution with observed
distribution for IW by KS-test, with overlaid histograms.
Original PostScript figures
(56 kB),
(56 kB)
We find that unbiased parameter estimates by 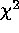 minimization are
possible for binned data with few or no counts in some bins, provided the
minimization are
possible for binned data with few or no counts in some bins, provided the
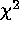 calculation is modified slightly. Except for
very small N, this modified
calculation is modified slightly. Except for
very small N, this modified 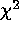 statistic is distributed
according to the theoretical
statistic is distributed
according to the theoretical 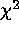 distribution. Goodness-of-fit can
therefore be assessed using traditional techniques. Further,
this
distribution. Goodness-of-fit can
therefore be assessed using traditional techniques. Further,
this 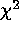 statistic can be used to estimate
confidence levels from standard
statistic can be used to estimate
confidence levels from standard 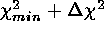 boundaries.
boundaries.
Acknowledgments:
This work is partially supported by NASA contract NAS5-30934.
References:
Cash, W. 1979 ApJ, 228, 939
Nousek, J. A., & Shue, D. R. 1989, ApJ, 342, 1207
Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P.
1986, Numerical Recipes (New York, Cambridge University Press)
Wheaton, W. A. et al. 1995, ApJ, submitted




 216 kB PostScript reprint
216 kB PostScript reprint
Next: A Method for
Up: Statistical Analysis
Previous: Cheating Poisson: A
adass4_editors@stsci.edu
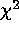 method and the C statistic. Use
of the
method and the C statistic. Use
of the 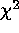 method requires that one avoid bins with 0 counts by
either ignoring them or rebinning, and produces significantly biased
results for data with few counts. The C-statistic gives unbiased results
but is difficult to interpret in terms of goodness-of-fit.
Neither approach is
ideal, though each is useful in some cases. The Iterative Weighting
Technique which we investigate here both addresses the
deficiencies inherent in using the standard method for data with few
counts, and provides a goodness-of-fit parameter which is
indistinguishable from the standard
method requires that one avoid bins with 0 counts by
either ignoring them or rebinning, and produces significantly biased
results for data with few counts. The C-statistic gives unbiased results
but is difficult to interpret in terms of goodness-of-fit.
Neither approach is
ideal, though each is useful in some cases. The Iterative Weighting
Technique which we investigate here both addresses the
deficiencies inherent in using the standard method for data with few
counts, and provides a goodness-of-fit parameter which is
indistinguishable from the standard 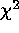 parameter for many datasets.
parameter for many datasets.
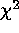 fitting technique,
useful for
fitting models to binned data with few counts per bin. We demonstrate
through numerical simulations that model parameters estimated with our
technique are essentially bias-free, even when the average number of
counts per bin is
fitting technique,
useful for
fitting models to binned data with few counts per bin. We demonstrate
through numerical simulations that model parameters estimated with our
technique are essentially bias-free, even when the average number of
counts per bin is 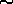 1. This is in contrast to the results from
traditional
1. This is in contrast to the results from
traditional 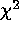 techniques, which exhibit significant biases in
such cases (see, for example, Nousek & Shue 1989; Cash 1979).
Moreover, our technique can explicitly handle bins with 0 counts,
obviating the need to ignore such bins or rebin the data. We conclude
with a discussion of the problem of estimating goodness-of-fit in the
limit of few counts using our modified
techniques, which exhibit significant biases in
such cases (see, for example, Nousek & Shue 1989; Cash 1979).
Moreover, our technique can explicitly handle bins with 0 counts,
obviating the need to ignore such bins or rebin the data. We conclude
with a discussion of the problem of estimating goodness-of-fit in the
limit of few counts using our modified 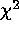 statistic.
statistic.
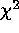 is expressed as a weighted sum of squared deviations,
is expressed as a weighted sum of squared deviations,
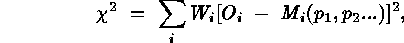
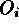 are the observed counts in bin i,
are the observed counts in bin i, 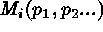 are
the counts predicted by the model M with parameters
are
the counts predicted by the model M with parameters 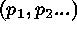 ,
and the weights
,
and the weights 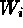 are the inverses of the true variances
are the inverses of the true variances
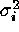 . As Wheaton et al. (1994) point out, the
approximation
. As Wheaton et al. (1994) point out, the
approximation 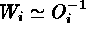 leads to significant biases in the
best-fit parameters, due to the strong anti-correlation between
leads to significant biases in the
best-fit parameters, due to the strong anti-correlation between 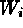 and
and 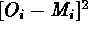 . Similar
biases are encountered if the approximation
. Similar
biases are encountered if the approximation 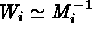 is
used (Nousek & Shue 1989).
The IW technique avoids such biases by estimating
is
used (Nousek & Shue 1989).
The IW technique avoids such biases by estimating 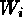 through
successive iterations, where for each iteration, j,
through
successive iterations, where for each iteration, j,
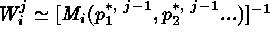 , and the best-fit
parameters
, and the best-fit
parameters 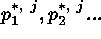 are determined by
minimization of
are determined by
minimization of
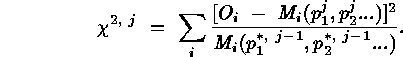
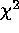 values
and
best-fit parameters converge after about 6 iterations.
values
and
best-fit parameters converge after about 6 iterations.
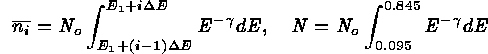
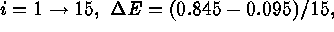 and
and 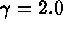 For each ideal spectrum, we simulate 1000 sample spectra {n
For each ideal spectrum, we simulate 1000 sample spectra {n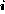 }, where
{n
}, where
{n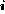 } are random deviates drawn from Poisson distributions with means
=
} are random deviates drawn from Poisson distributions with means
= 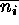 . We then determine best-fit model parameters
. We then determine best-fit model parameters
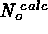 and
and
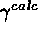 for each simulated spectrum, using IW
and Powell's method for function minimization (Press 1988). For
each N, we then compute
the average
for each simulated spectrum, using IW
and Powell's method for function minimization (Press 1988). For
each N, we then compute
the average 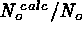 and
and 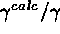 ; compile the
distributions of minimum
; compile the
distributions of minimum 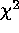 for comparison with the theoretical
distribution; and compute the percentage of simulations for which the
for comparison with the theoretical
distribution; and compute the percentage of simulations for which the
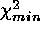 and
and 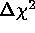 contours include
contours include 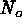 and
and 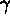 ,
for comparison with the expected percentages.
,
for comparison with the expected percentages.

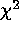 and the C statistic by Nousek & Shue in 250 runs.
We find that the IW biases are comparable to those encountered using
the C statistic for all N. These results are displayed in
Figure
and the C statistic by Nousek & Shue in 250 runs.
We find that the IW biases are comparable to those encountered using
the C statistic for all N. These results are displayed in
Figure 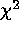 distributions with our observed
distributions. We apply a KS-test to the cumulative distributions and
find that at N=25 the match is poor, but by
N=100 the two distributions are in good agreement.
distributions with our observed
distributions. We apply a KS-test to the cumulative distributions and
find that at N=25 the match is poor, but by
N=100 the two distributions are in good agreement.
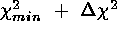 contours include
contours include 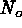 and
and 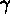 ,
for
,
for 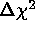 values appropriate to various joint two-parameter
confidence levels, is shown in
table
values appropriate to various joint two-parameter
confidence levels, is shown in
table 
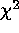 Boundaries, from a total of 1000 spectral fits.
Boundaries, from a total of 1000 spectral fits.

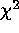 distribution with observed
distribution for IW by KS-test, with overlaid histograms.
Original PostScript figures
distribution with observed
distribution for IW by KS-test, with overlaid histograms.
Original PostScript figures
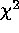 minimization are
possible for binned data with few or no counts in some bins, provided the
minimization are
possible for binned data with few or no counts in some bins, provided the
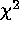 calculation is modified slightly. Except for
very small N, this modified
calculation is modified slightly. Except for
very small N, this modified 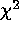 statistic is distributed
according to the theoretical
statistic is distributed
according to the theoretical 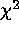 distribution. Goodness-of-fit can
therefore be assessed using traditional techniques. Further,
this
distribution. Goodness-of-fit can
therefore be assessed using traditional techniques. Further,
this 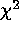 statistic can be used to estimate
confidence levels from standard
statistic can be used to estimate
confidence levels from standard 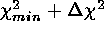 boundaries.
boundaries.