In recent years, various techniques developed in the field of artificial intelligence have been applied to the analysis of astronomical data, in an attempt to cope with the problem posed by the information overload created by the presence of numerous and sophisticated astronomical data collection devices. By far the most commonly used approach has been artificial neural networks. Neural networks have been used for spectral classification of stars (Gulati et al. 1995; Bailer-Jones et al. 1998), for morphological classification of galaxies (Naim et al. 1995), for discriminating stars and galaxies in deep-field photographs, and for unsupervised classification of the astronomical literature. While they have had remarkably good results in some problem domains, they present some drawbacks that make the investigation of alternative and complementary automated methods desirable. A shortcoming of neural networks is that the time required to train a network can be very long. Also, since they perform local search in parameter space, they often converge to local minima. A final drawback is that once trained, neural networks can only be viewed as black boxes, in the sense that it is very difficult for humans to interpret the rules learned by the network. In this paper we explore instance-based methods, which do not require the long training times of neural networks, while providing similar and often higher levels of performance.
Several of the most commonly used learning algorithms, such as neural networks and decision trees, use their training examples to construct an explicit global representation of the target function. In contrast, instance-based learning algorithms simply store some or all of the training examples and postpone any generalization effort until a new instance must be classified. They can thus build query-specific local models, which attempt to fit the training examples only in a region around the query point.
Metric distance minimization(MDM) is perhaps the simplest instance-based learning method. In MDM, when a query is presented, we find the training example that is closest to the query point, in terms of the Euclidean distance or some other suitable metric, and provide the parameters of that example as predicted output parameters.
K-nearest-neighbors (KNN) is a generalization of metric distance minimization. Instead of returning the parameters of the point that is most similar to the query point, KNN returns the average of the parameters of its (k) nearest neighbors, again defined in terms of Euclidean distance. A straight-forward extension to this approach is distance-weighted nearest neighbors, in which instead of a straight average, we take a weighted average of the output parameters of the nearest neighbors, with the weight factor usually being the inverse of the distance from each neighbor to the query point.
Locally Weighted Regression (LWR) uses examples that are close
to the query point, weighted according to their distance, and builds a
model in the vicinity of that point. This local approximation can be a
linear function, a quadratic function or even a multilayer neural net.
In this work we use a local linear model around the query point to
approximate the target function. We assume that the weight of each
training point is given by the inverse of the square distance from the
training point to the query point:
![]() . Let
. Let ![]() be a diagonal matrix, let
be a diagonal matrix, let ![]() be the training
data, then the weighted training data are given by
be the training
data, then the weighted training data are given by ![]() and the
weighted target function is
and the
weighted target function is ![]() Subsequently we use the
estimator for the target function
Subsequently we use the
estimator for the target function
![]()
Instance-Based Learning with PCA Preprocessing. One way to
reduce the computational cost of considering all attributes is to
pre-process the data with principal component analysis (PCA). PCA
finds a set of basis vectors, given by the ![]() eigenvectors of the
covariance matrix of the data with the largest associated eigenvalues,
that optimally represent the
eigenvectors of the
covariance matrix of the data with the largest associated eigenvalues,
that optimally represent the ![]() dimensional original data set. This
projection is then used as input to the learning algorithm.
dimensional original data set. This
projection is then used as input to the learning algorithm.
Jones (1996) has produced an homogeneous catalog of spectral indices
for 684 stars observed at KPNO with the coudé feed instrument. The
spectral indices were measured from the spectra in the wavelength
regions
![]() and
and
![]() by following
definition of the Lick indices (Worthey et al. 1994), the Rose
indices (Rose 1994) and new Lick-type Balmer indices (Jones &
Worthey 1995). In our application, we used the indices in
conjunction with physical atmospheric parameters given in the catalog.
by following
definition of the Lick indices (Worthey et al. 1994), the Rose
indices (Rose 1994) and new Lick-type Balmer indices (Jones &
Worthey 1995). In our application, we used the indices in
conjunction with physical atmospheric parameters given in the catalog.
We implemented metric distance minimization, distance-weighted k-nearest-neighbors and locally weighted regression algorithms and applied them to the data set described in the previous section. We also tested the effects of adding a PCA preprocessing stage, choosing the first eight principal components, before applying the three algorithms.
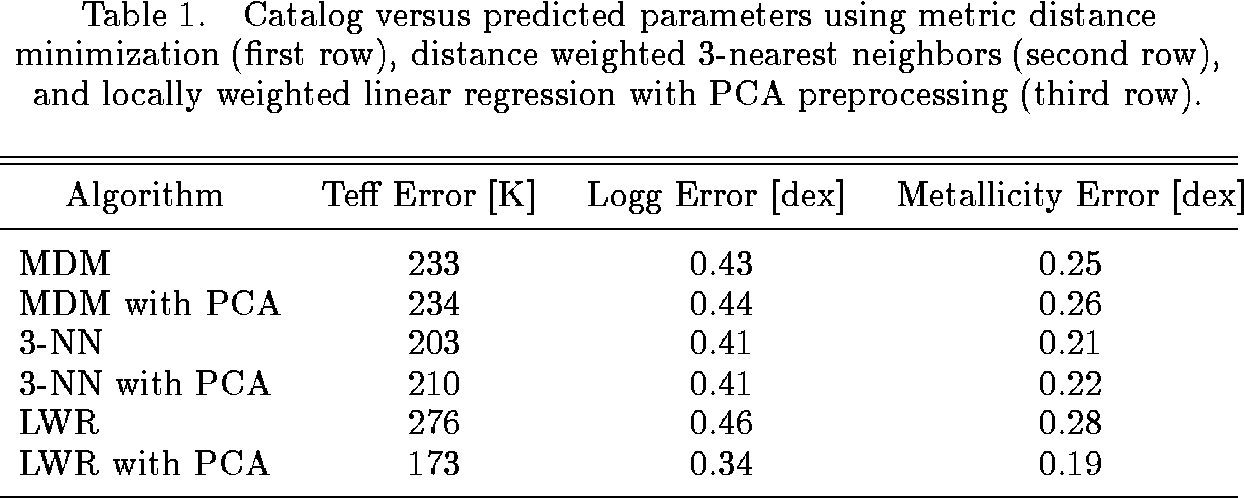
We used a leave-one-out-cross-validation approach for testing. This means that to predict a star's parameters we used the data for all the other stars in the database. Table 1 shows the root mean squared errors obtained in the prediction of effective temperature, surface gravity and metallicity from the spectral indices, with and without PCA preprocessing.
 |
The results show that 3NN and LWR significantly improve upon the results obtained by applying metric distance minimization. It can also be seen that PCA preprocessing does not appear to improve the performance of MDM and KNN, but greatly improves the performance of LWR. Overall, the best results are obtained applying LWR with PCA preprocessing, which reduces the error by about 25% compared to standard MDM and by about 15% compared to 3NN.
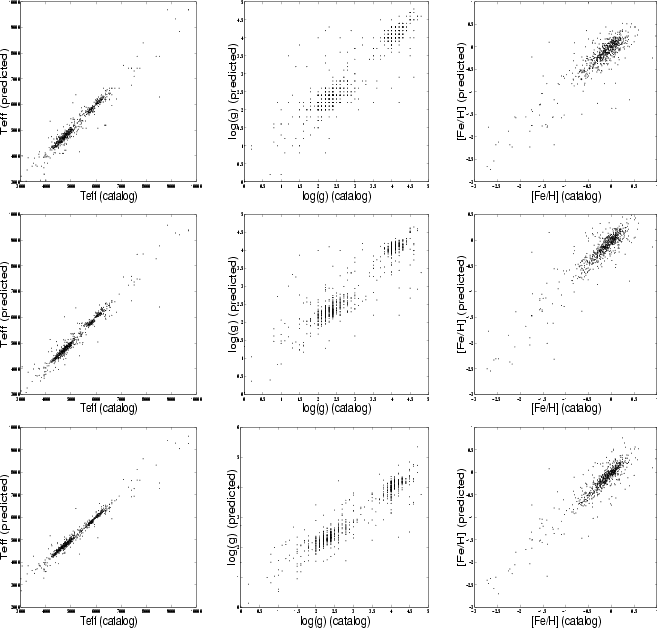
Figure 1 shows the catalog versus predicted stellar parameters using standard metric distance minimization algorithm, distance-weighted 3-nearest neighbors and locally weighted regression with PCA preprocessing. A perfect fit corresponds to a diagonal line. It can be seen that LWR gives a notably smaller dispersion, as expected from the root mean squared error results.
Our results show that instance-based learning methods can be used to predict with very good accuracy the effective temperature, surface gravity and metallicity of stars given spectral indices. Of the methods tested, we found that using principal component pre-processing, combined with locally weighted regression, gives the best results.
Bailer-Jones, C. A. L., Irwin, M., & Von Hippel, T. 1998, MNRAS, 298,361
Gulati, K., Gupta, R., Gothoskar, P., & Khobragade, S. 1995, in ASP Conf. Ser., Vol. 77, Astronomical Data Analysis Software and Systems IV, ed. R. A. Shaw, H. E. Payne, & J. J. E. Hayes (San Francisco: ASP), 253
Jones, L. A. & Worthey, G. 1995, ApJ, 446, 31
Jones, L. A. 1996, Ph. D. Thesis, University of North Carolina, Chapel Hill
Naim, A., Lahav, O., Sodré Jr., L., & Storrie-Lombardi, M. C. 1995, MNRAS 275, 567
Rose, A. J. 1994, AJ, 107, 206
Worthey, G., Faber, S. M., González, J. J., & Burstein, D. 1994, ApJS, 94, 687