
A. C. Phillips
Lick Observatory, University of California, Santa Cruz, CA, 95064
L. E. Davis
National Optical Astronomy Observatories, P. O. Box 26732, Tucson,
AZ 85726
A variety of astronomical programs involve comparing similar image data of the same field. Examples include searches for extragalactic novae, supernovae and variable stars; continuum-subtraction for narrow-band emission-line images; and production of color or polarization maps, to name a few of the more obvious cases. For these types of observations, it is usually essential that all observational differences be eliminated before comparison. While instrumental signatures can be removed accurately, varying conditions (e.g., seeing, transparency) are more problematic. This is particularly crucial where the objects of interest are either extended or are found in regions of strong background gradients.
The process of ``matching'' an image to a reference image requires: (1) applying a geometric transformation to spatially register an image to the reference image; (2) convolving the registered image with an appropriate kernel to degrade the point-spread function to match that of the reference image; and (3) scaling and offsetting the intensity of the convolved image to match the intensity and background sky level of the reference image.
We have developed a set of IRAF tasks to compute and apply the necessary transformations for image matching. In this paper we briefly describe the algorithms and tasks and illustrate the software with a pair of images obtained under different seeing conditions. We conclude by describing the current status and future development plans of the software.
The current software performs spatial registration by supplying the registration task with a reference and input image list, and a list of features common to both images. Two spatial registration tasks are available: a ``polynomial warping'' procedure for general cases, and a new cross-correlation task for the special case that only translations are required.
The polynomial warping task is an IRAF script which combines existing IRAF object selecting, centering, and geometric transformation tasks. This task is required for the general case that pixel scales and/or orientation differ between the input and reference images. The user supplies this task with a set of star positions in the reference image, and the positions of two stars in both the reference and input images. The task computes an initial transformation using the two specified stars, refines it using the full reference star list, and applies the computed transformation to the input image.
If the input and reference images have identical pixel scales and orientation, they can be registered using the cross-correlation task. The user supplies this task with a list of rectangular image regions, each containing high signal-to-noise features suitable for cross-correlation. The task computes the shift from the cross-correlation function and applies it to the input image.
Point-spread function (PSF) variations have many sources: seeing changes, guiding errors and focus variations are the most common. Removing the PSF differences is easy in principle but difficult in practice. If r is the reference image, i is the (spatially-registered) input image, and R and I are their Fourier transforms, then

and the Convolution Theorem gives us

where k is some convolution kernel describing the difference in seeing, etc., and K is its Fourier transform. k also contains scaling information for differences in exposure and transparency. The unknown kernel k is then given simply by

In practice, unfortunately, the high-frequency components of the images are dominated by noise and so the ratio in Fourier space is poorly behaved. We have found that satisfactory results can obtained by replacing the high-frequency components with a Gaussian model fit to the lower-frequency (higher signal-to-noise) components. This approximation, as well as many other considerations, are discussed in Phillips (1993b).
In principle, the kernel k can be used to deconvolve an image to match a better-seeing image, but in practice, noise is again a severe problem, and deconvolution is a costly procedure. Degrading the better-seeing image is usually acceptable. The convolution smooths the noise as well as the object signal, so only contrast---not signal-to-noise---is lost.
Two PSF-matching options are available in our IRAF task. Both require the reference image to have lower resolution than the input image. In the first, the user must supply the task with the reference and input image and a list of high signal-to-noise point sources. In the second, the user must supply pre-computed PSFs for the reference and input images. (Pre-computed PSFs may be derived from other IRAF software such as the DAOPHOT package or be computed by the user.) In both cases, the task computes the required kernel and performs the convolution. The PSF-matching task also includes options for removing the background around the input point sources, as well as control over the replacement of the high-frequency components with the Gaussian model.
Many image matching problems require the final images to have the same intensity scale. The current software requires the input and reference images to be spatially-registered and PSF-matched. The user specifies a rectangular data region which contains both object and (ideally) sky data. The task uses linear least squares techniques (including a user-supplied noise model for both images, and automatic deviant pixel rejection) to compute the required scale factor and zero point offset, and applies the transformation.
Figure 1 shows two B-band images of the Phoenix dwarf galaxy at different epochs (top). Also shown are the difference image after registration and intensity matching only (bottom left), and the same with PSF-matching (right). In the fully-matched case, about a dozen Cepheids variables are easily seen. Note also the high-proper motion star just below and left of the center. Additional illustrations may be found elsewhere (Phillips 1993a,b; Margon et al. 1992; Ruiz et al. 1987).
A prototype version of this software is currently available from A. Phillips ( phillips@lick.ucsc.edu) on a use at your own risk basis. Prospective users should be aware that the software is unsupported and minimally documented, although the author welcomes comments and suggestions for improvement.
The cross-correlation task for spatial registration will be included in the next release of IRAF, and is already available to users as add-on software. A new version of the PSF-matching task is nearing completion and will be available as add-on software shortly after this meeting. Contact L. Davis ( davis@noao.edu) for a status report.
Future plans include modifying the cross-correlation task to handle images with small scale and orientation differences and adding the intensity scaling task to IRAF itself.
ACP wishes to thank NOAO for providing him support as a Visiting Specialist during the summer of 1988, when the PSF-matching algorithm and software were developed. He also thanks the IRAF group for their hospitality and patient instruction during that time.
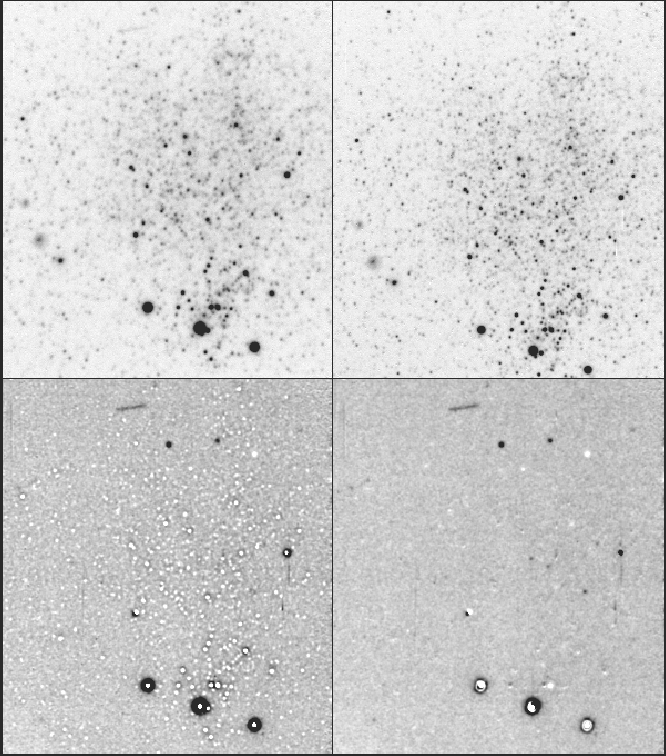
Figure:
Searching for Cepheid variables in the Phoenix dwarf galaxy.
See text. (CTIO 4-m images courtesy of Nelson Calwell.)
Original PostScript figure (830 kB)
Phillips, A. C. 1993a, AJ, 105, 486
Phillips, A. C. 1993b, PhD Dissertation, University of Washington, Seattle
Ruiz, M. T., Blanco, V., Maza, J., Heathcote, S., Phillips, A., Kawara, K., Anguita, C., Hamuy, M., & Gómez, A. 1987, ApJ, 316, L21