



 1160 kB PostScript reprint
1160 kB PostScript reprint
Next: RegisteringPSF-Matching and
Up: Image Restoration and
Previous: Improvements in Filter
Astronomical Data Analysis Software and Systems IV
ASP Conference Series, Vol. 77, 1995
Book Editors: R. A. Shaw, H. E. Payne, and J. J. E. Hayes
Electronic Editor: H. E. Payne
R. N. Hook and L. B. Lucy
Space Telescope--European Coordinating Facility, European Southern
Observatory, Karl-Schwarzschild-Str. 2, D-85748 Garching bei München, Germany
Affiliated with the Astrophysics Division, Space Science
Department, European Space Agency
Abstract:
Crowded-field stellar photometry consists of three main phases:
locating the point sources, determining the point spread function (PSF) and
measuring the point source brightnesses. In earlier work (Lucy 1994; Hook &
Lucy 1994) we have described a two-channel
restoration method which provides photometric fidelity and addresses the last
of these items in a restoration context. Here we describe two further
enhancements. First, an experimental method for locating stellar images by
enhancing the sharp cores of stars using a multi-channel entropy
minimization
technique is described. In addition an extended version of the two-channel
method is given which allows PSFs to be extracted from designated
point-sources in images during restoration. A default PSF may be
used to regularize the result. A simple but accurate model for the form of
ground-based PSFs (Saglia et al. 1993) has been implemented and seems a
suitable choice of default PSF for ground-based images. Examples
using a typical ground-based CCD image of a star cluster are given.
These methods are available in preliminary implementations running within
both the IRAF and MIDAS data analysis packages.
In earlier papers (Lucy 1994; Hook & Lucy 1994) we described a
two-channel restoration method
in which one channel contains point-sources and the other
contains a smooth background to represent the sky or an extended object.
The second channel is regularized by the addition of an entropy term to
the expression being maximized, but the first is treated as a simple
likelihood maximization. This method has many advantages including the
suppression of the artifacts often seen around bright stars in conventional
single channel restorations and photometric fidelity without the bias
found in most restoration techniques (e.g., Cohen 1991).
The technique of multiple channels with different regularization is here
extended in two directions of relevance to crowded field photometry. First
an experimental three-channel method is described in which one channel
has a negative
coefficient for the entropy term. This has the opposite effect to the
normal smoothing which follows from positive entropy coefficients and
enhances point sources, ultimately to the point where they become
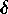 -functions (single pixels or sub-pixels). Secondly, ways of
extracting a PSF from an image
containing designated point-sources are described as well as
different ways in which such a PSF may be regularized. An implementation of a
recently suggested theoretical form for the PSF of ground-based telescopes
is available and is suitable for use as a default PSF.
-functions (single pixels or sub-pixels). Secondly, ways of
extracting a PSF from an image
containing designated point-sources are described as well as
different ways in which such a PSF may be regularized. An implementation of a
recently suggested theoretical form for the PSF of ground-based telescopes
is available and is suitable for use as a default PSF.
Maximum likelihood restorations often develop noise ``spikes'' when large
numbers of iterations are used and regularization methods, often based on
maximizing an entropy expression, are used to impose smoothness. However,
point sources in images are really 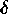 -functions on the sky and hence
are the opposite of smooth. This suggests a method for finding point sources
using an entropy minimization rather than the normal maximization used
to impose smoothness. In this case an objective function of the
following form is maximized:
-functions on the sky and hence
are the opposite of smooth. This suggests a method for finding point sources
using an entropy minimization rather than the normal maximization used
to impose smoothness. In this case an objective function of the
following form is maximized:
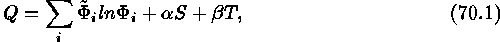
where 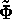 is the observed intensity distribution,
is the observed intensity distribution, 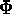 is the current estimate and the summation
is performed over all pixels in the image. The first term is the likelihood,
and S and T are entropy-type expressions.
The second term has positive
is the current estimate and the summation
is performed over all pixels in the image. The first term is the likelihood,
and S and T are entropy-type expressions.
The second term has positive
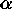 and acts as a standard regularization to enforce smoothness on the
background channel. The third term has
and acts as a standard regularization to enforce smoothness on the
background channel. The third term has 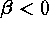 and leads to a minimization
of the entropy of a ``points'' channel. Both entropy expressions are evaluated
relative to floating priors, the second term relative to a highly smoothed
version of the total estimated intensity in the image and the third
relative to a slightly smoothed version of the current estimate for the
points channel. It is necessary to choose the parameters
and leads to a minimization
of the entropy of a ``points'' channel. Both entropy expressions are evaluated
relative to floating priors, the second term relative to a highly smoothed
version of the total estimated intensity in the image and the third
relative to a slightly smoothed version of the current estimate for the
points channel. It is necessary to choose the parameters 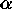 and
and 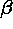 ,
as well as the degree of smoothing applied when creating the floating defaults,
so that even faint points are successfully found but noise clumps are not
detected. An experimental implementation has been coded as a program
called stars. Unlike normal star finding methods which seek local
maxima this method is global and works on the entire image.
,
as well as the degree of smoothing applied when creating the floating defaults,
so that even faint points are successfully found but noise clumps are not
detected. An experimental implementation has been coded as a program
called stars. Unlike normal star finding methods which seek local
maxima this method is global and works on the entire image.

Figure: An example of star finding: see text for details.
Original PostScript figure (680 kB)
Figure 1 ( left) shows a typical deep CCD image of a star cluster.
This frame is part of an I-band image of the cluster M71 taken by F. G.
Jensen (Aarhus) using the Nordic Optical Telescope, and used with his
permission. Figure 1 ( center) shows the points (low entropy) channel
produced by applying this method to Figure 1 ( left), and Figure 1
( right) shows the smooth (high
entropy) background channel obtained simultaneously. All the stars visible to
the eye in the input have been found and there are few spurious detections.
The background smooth image shows small artifacts caused by the displacements
of the stars from the centers of pixels.
This map of the star positions may then be used directly as input to the
PLUCY two-channel code to obtain unbiased magnitudes for the designated
point-sources.
Successful image restoration and photometry both require a good knowledge
of the PSF. Many restoration methods can
be generalized to allow simultaneous ``blind iterative restoration'' in
which the PSF is obtained simultaneously with the restored image. Such methods
are generally thought to be unreliable and are little used. However, when
the additional information of designated point-sources is added much greater
robustness and reliability is achieved. Such simultaneous PSF determination
can easily be added to the PLUCY two-channel code and a preliminary example
of its use on HST data is given in Hook & Lucy (1994).
Such results tend to retain noise features from the data frames, particularly
around bright stars, and are clearly not optimal. It would be advantageous
to use extra information about the PSF expected and also to provide
regularization to produce a resultant PSF which is smooth. The code
has now been updated to include such regularization and found to be effective.
We now need a suitable choice of form for the regularizing, default PSF.
Several models for ground-based PSFs have been proposed and used. These are
typically simple analytic functions (such as the Moffat function or
multiple Gaussians) which may
be conveniently fitted to stars but do not have any physical basis. However,
recently Saglia et al. (1993) have investigated another form for such PSFs
which can be derived from the theory of atmospheric seeing and they show
that this form fits observed PSFs as well as, if not better than, the more
traditional ad hoc forms. This new form has only
two parameters (one of which is simply the size of the star images as defined
by the FWHM) but has the minor disadvantage of not being analytic, being instead
the Fourier transform of a simple exponential function. This form for the PSF
has been implemented as an IRAF compatible task called ``seeing'' and
seems an excellent choice for a default PSF.

Figure: PSF Determination---see text for details.
Original PostScript figure (422 kB)
Figure 2 shows the steps in the derivation of a good PSF from the same M71
image used above. First the FWHM of bright (but unsaturated) stars in the
frame is measured. This value is then used to produce a default PSF of the
Saglia et al. (1993) form ( upper-right). This in turn is used as the
default PSF with the PLUCY code to finally give the required best estimate
for the PSF ( lower-left). A simple circular disc is used as the first
approximation for the PSF ( upper-left). A clear elongation
of the images has been well modelled and the result is smooth and free of
noise features. The PSF found by DAOPHOT, using the same input data, is given
at the lower-right for comparison.
We have extended earlier work on multi-channel, regularized image restoration
to produce experimental codes which allow both the mapping of point-source
positions in an image and the estimation of the PSF during
a subsequent photometric image restoration. A recently suggested form for
ground-based
PSFs has been implemented and found to be a suitable default. Tests have
successfully been made using a typical deep, ground-based CCD frame. All codes
have been implemented using the F77/VOS interface to IRAF and are available
on request.
References:
Cohen, J. G. 1991, AJ, 101, 734
Hook, R. N. & Lucy, L. B. 1994,
in The Restoration of HST Images and Spectra II,
ed. R. J. Hanisch & R. L. White (Baltimore,
Space Telescope Science Institute), p. 86
Lucy, L. B. 1994, in The Restoration of HST Images and Spectra II,
ed. R. J. Hanisch & R. L. White (Baltimore,
Space Telescope Science Institute), p. 79
Saglia, R. P., et al. 1993, MNRAS, 264, 961




 1160 kB PostScript reprint
1160 kB PostScript reprint
Next: RegisteringPSF-Matching and
Up: Image Restoration and
Previous: Improvements in Filter
adass4_editors@stsci.edu
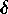 -functions (single pixels or sub-pixels). Secondly, ways of
extracting a PSF from an image
containing designated point-sources are described as well as
different ways in which such a PSF may be regularized. An implementation of a
recently suggested theoretical form for the PSF of ground-based telescopes
is available and is suitable for use as a default PSF.
-functions (single pixels or sub-pixels). Secondly, ways of
extracting a PSF from an image
containing designated point-sources are described as well as
different ways in which such a PSF may be regularized. An implementation of a
recently suggested theoretical form for the PSF of ground-based telescopes
is available and is suitable for use as a default PSF.
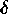 -functions on the sky and hence
are the opposite of smooth. This suggests a method for finding point sources
using an entropy minimization rather than the normal maximization used
to impose smoothness. In this case an objective function of the
following form is maximized:
-functions on the sky and hence
are the opposite of smooth. This suggests a method for finding point sources
using an entropy minimization rather than the normal maximization used
to impose smoothness. In this case an objective function of the
following form is maximized:
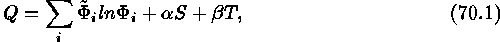
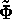 is the observed intensity distribution,
is the observed intensity distribution, 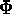 is the current estimate and the summation
is performed over all pixels in the image. The first term is the likelihood,
and S and T are entropy-type expressions.
The second term has positive
is the current estimate and the summation
is performed over all pixels in the image. The first term is the likelihood,
and S and T are entropy-type expressions.
The second term has positive
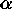 and acts as a standard regularization to enforce smoothness on the
background channel. The third term has
and acts as a standard regularization to enforce smoothness on the
background channel. The third term has 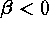 and leads to a minimization
of the entropy of a ``points'' channel. Both entropy expressions are evaluated
relative to floating priors, the second term relative to a highly smoothed
version of the total estimated intensity in the image and the third
relative to a slightly smoothed version of the current estimate for the
points channel. It is necessary to choose the parameters
and leads to a minimization
of the entropy of a ``points'' channel. Both entropy expressions are evaluated
relative to floating priors, the second term relative to a highly smoothed
version of the total estimated intensity in the image and the third
relative to a slightly smoothed version of the current estimate for the
points channel. It is necessary to choose the parameters 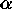 and
and 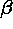 ,
as well as the degree of smoothing applied when creating the floating defaults,
so that even faint points are successfully found but noise clumps are not
detected. An experimental implementation has been coded as a program
called stars. Unlike normal star finding methods which seek local
maxima this method is global and works on the entire image.
,
as well as the degree of smoothing applied when creating the floating defaults,
so that even faint points are successfully found but noise clumps are not
detected. An experimental implementation has been coded as a program
called stars. Unlike normal star finding methods which seek local
maxima this method is global and works on the entire image.

