



 160 kB PostScript reprint
160 kB PostScript reprint
Next: Automated Spectral Reduction
Up: Data Modeling and
Previous: Towards a General
Astronomical Data Analysis Software and Systems IV
ASP Conference Series, Vol. 77, 1995
Book Editors: R. A. Shaw, H. E. Payne, and J. J. E. Hayes
Electronic Editor: H. E. Payne
J. Bland-Hawthorn
Anglo-Australian Observatory, P.O. Box 296,
Epping, N.S.W. 2121 Australia
S. Serjeant
Department. of Astrophysics, University of Oxford, Oxford
OX1 3RH, UK
P. L. Shopbell
Department. of Space Physics & Astronomy, Rice University,
P.O. Box 1892, Houston, TX 77251
Abstract:
It is notoriously difficult to identify weak cosmic ray events in long
exposure observations. The majority of ``de-glitch" programs have little
difficulty in identifying the bright events. The faint events---either
individual or ``splatter'' around bright events---are rather more problematic.
We propose a simple test to evaluate the effectiveness of a de-glitch program
in removing weak events. The method is to compare the probability distribution
function (PDF) of cosmic ray events between an observation and a dark frame
matched in exposure time. We illustrate the basic idea using dark exposures
from a Tek 1024 1024 CCD with varying exposure lengths and read-out
times.
1024 CCD with varying exposure lengths and read-out
times.
We have obtained dark frames using the Tek 1024 1024 CCD at the
AAT 3.9m with varying exposure lengths (15, 30, 60, and 120min) and read-out
times (FAST, SLOW, XTRASLOW). The histogram
of each frame shows the contribution from the bias, read and dark noise. A
millisecond exposure was used to remove the bias and read noise contribution
to each histogram. The additional contribution from the dark noise is well
calibrated at 0.11countspix
1024 CCD at the
AAT 3.9m with varying exposure lengths (15, 30, 60, and 120min) and read-out
times (FAST, SLOW, XTRASLOW). The histogram
of each frame shows the contribution from the bias, read and dark noise. A
millisecond exposure was used to remove the bias and read noise contribution
to each histogram. The additional contribution from the dark noise is well
calibrated at 0.11countspix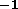 ksec
ksec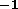 . It is assumed that the
remaining events are related to cosmic rays. Only half the CCD frame was
used because long exposures revealed a weak intensity gradient
in the dark response on the other half.
. It is assumed that the
remaining events are related to cosmic rays. Only half the CCD frame was
used because long exposures revealed a weak intensity gradient
in the dark response on the other half.
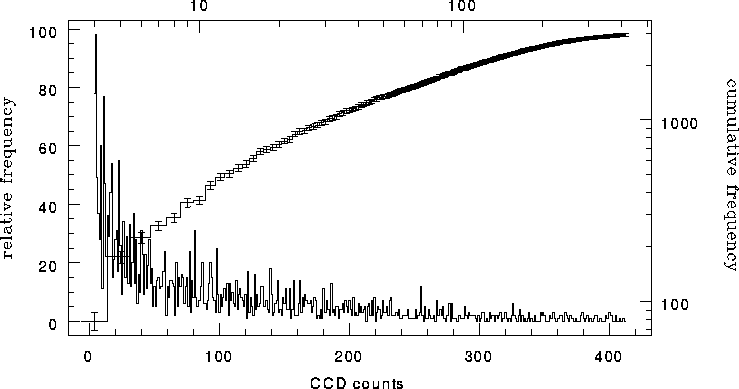
Figure: Histogram of cosmic ray events in a two hour dark frame. The monotonic
curve is the cumulative histogram of these events. The error bars
are Poissonian and not independent.
Original PostScript figure (78 kB)
We define 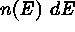 to be the number of cosmic ray events with energies
(expressed in counts) in the range
to be the number of cosmic ray events with energies
(expressed in counts) in the range 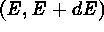 . The cumulative distribution
is then
. The cumulative distribution
is then

When 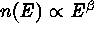 , the slope
of the plot
, the slope
of the plot 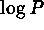 vs
vs 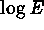 is proportional to
is proportional to 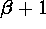 .
In Figure
.
In Figure  , the noisy histogram is the bias/dark/read noise
subtracted dark frame. The monotonic curve is a plot of
, the noisy histogram is the bias/dark/read noise
subtracted dark frame. The monotonic curve is a plot of 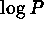 vs.
vs. 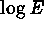 which is found to be rather well defined and reproducible over the different
exposures. We propose that de-glitch programs should compute the PDF in this
way for both the data and a matched dark frame (same exposure, same read-out
time). The PDF for the data is determined from all events identified by the
de-glitch algorithm. Since the energetic events are easier to find, the bright
end of both PDFs will be well matched. In Figure
which is found to be rather well defined and reproducible over the different
exposures. We propose that de-glitch programs should compute the PDF in this
way for both the data and a matched dark frame (same exposure, same read-out
time). The PDF for the data is determined from all events identified by the
de-glitch algorithm. Since the energetic events are easier to find, the bright
end of both PDFs will be well matched. In Figure  , where the
de-glitch PDF turns over at low energy---presumably but not necessarily at an
energy greater than or equal to the turnover in the dark PDF---gives some idea
as to how effective the algorithm has been in removing the weaker events.
, where the
de-glitch PDF turns over at low energy---presumably but not necessarily at an
energy greater than or equal to the turnover in the dark PDF---gives some idea
as to how effective the algorithm has been in removing the weaker events.
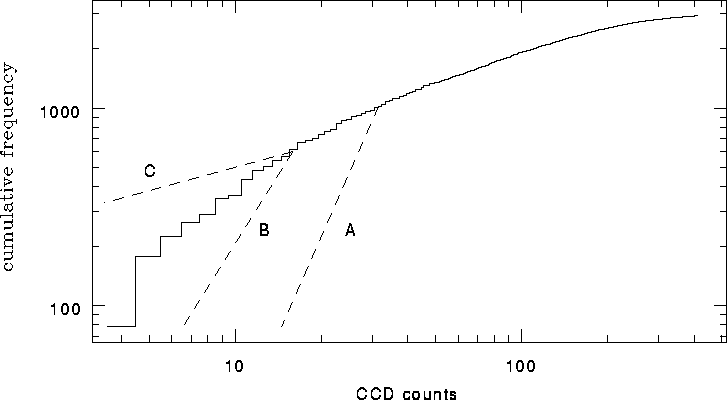
Figure: The cumulative histogram from Figure  with which
to compare the performance of a de-glitch algorithm. Three cases are
illustrated: algorithm A is too conservative, algorithm B more reliable, and
algorithm C has mistaken real data with faint cosmic rays.
Original PostScript figure (16 kB)
with which
to compare the performance of a de-glitch algorithm. Three cases are
illustrated: algorithm A is too conservative, algorithm B more reliable, and
algorithm C has mistaken real data with faint cosmic rays.
Original PostScript figure (16 kB)




 160 kB PostScript reprint
160 kB PostScript reprint
Next: Automated Spectral Reduction
Up: Data Modeling and
Previous: Towards a General
adass4_editors@stsci.edu
 1024 CCD at the
AAT 3.9m with varying exposure lengths (15, 30, 60, and 120min) and read-out
times (FAST, SLOW, XTRASLOW). The histogram
of each frame shows the contribution from the bias, read and dark noise. A
millisecond exposure was used to remove the bias and read noise contribution
to each histogram. The additional contribution from the dark noise is well
calibrated at 0.11countspix
1024 CCD at the
AAT 3.9m with varying exposure lengths (15, 30, 60, and 120min) and read-out
times (FAST, SLOW, XTRASLOW). The histogram
of each frame shows the contribution from the bias, read and dark noise. A
millisecond exposure was used to remove the bias and read noise contribution
to each histogram. The additional contribution from the dark noise is well
calibrated at 0.11countspix ksec
ksec . It is assumed that the
remaining events are related to cosmic rays. Only half the CCD frame was
used because long exposures revealed a weak intensity gradient
in the dark response on the other half.
. It is assumed that the
remaining events are related to cosmic rays. Only half the CCD frame was
used because long exposures revealed a weak intensity gradient
in the dark response on the other half.
 1024 CCD with varying exposure lengths and read-out
times.
1024 CCD with varying exposure lengths and read-out
times.

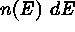 to be the number of cosmic ray events with energies
(expressed in counts) in the range
to be the number of cosmic ray events with energies
(expressed in counts) in the range 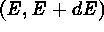 . The cumulative distribution
is then
. The cumulative distribution
is then

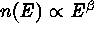 , the slope
of the plot
, the slope
of the plot 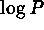 vs
vs 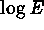 is proportional to
is proportional to 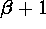 .
In Figure
.
In Figure 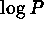 vs.
vs. 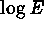 which is found to be rather well defined and reproducible over the different
exposures. We propose that de-glitch programs should compute the PDF in this
way for both the data and a matched dark frame (same exposure, same read-out
time). The PDF for the data is determined from all events identified by the
de-glitch algorithm. Since the energetic events are easier to find, the bright
end of both PDFs will be well matched. In Figure
which is found to be rather well defined and reproducible over the different
exposures. We propose that de-glitch programs should compute the PDF in this
way for both the data and a matched dark frame (same exposure, same read-out
time). The PDF for the data is determined from all events identified by the
de-glitch algorithm. Since the energetic events are easier to find, the bright
end of both PDFs will be well matched. In Figure 