The proposed method based on the orthogonal representation of the equations of a model is free of this fault since it tests the consistency of the model and data.
This method have been used to find out the compatibility of the standard kinematical model with the proper motions of stars in the Hipparcos catalogue. It shows that there are some difficulties with the standard model of the Galactic rotation, and, on the contrary, there is a good agreement with the model of the Sun motion.
A common practice in astronomy is: gathering data, constructing a model, evaluating of the parameters of the model by the Least Squares technique.
Let us take an example from stellar kinematics. Usually, we have
a catalogue, which contains coordinates (l, b) and proper motions
(
![]() ) of stars. General model of proper motions describes
the Sun motion and the galactic rotation and may be represented as
) of stars. General model of proper motions describes
the Sun motion and the galactic rotation and may be represented as
The main condition of correct use of the LST is: ``![]() in the
formula (1) is nothing else but the Gaussian noise''.
We forget this very often since the LST always does produce a result,
but it may be
in the
formula (1) is nothing else but the Gaussian noise''.
We forget this very often since the LST always does produce a result,
but it may be
We call equation (2) the physical model of
proper motions where functions ![]() form the functional basis of
the model
form the functional basis of
the model ![]() . Let us consider the formal model of
proper motions with another functional basis
. Let us consider the formal model of
proper motions with another functional basis ![]() :
:
Good agreement between the values derived from several harmonics shows the correspondence of the model to observations.
Bad agreement can show:
In addition, the existence of unpredictable non-zero coefficients indicates that adopted model is not complete.
Concerning the basis ![]() , we have to choose such set of functions
which being applied to the physical basis, produces the relations
like (3). Usually, in stellar kinematics, the spherical
functions are good.
, we have to choose such set of functions
which being applied to the physical basis, produces the relations
like (3). Usually, in stellar kinematics, the spherical
functions are good.
The Oort-Linblad's model is widely used for the analysis of proper motions.
The general view of the equation for proper motions in the galactic
longitude is
| (4) |
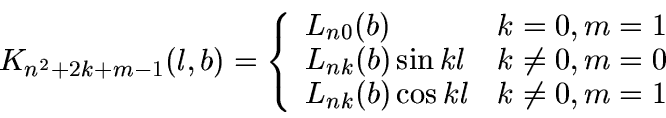 |
(5) |
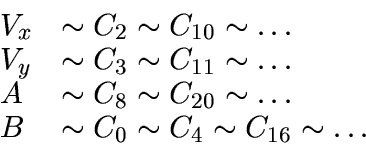 |
(6) |
In some models (for example, three-dimensional rotation of the Galaxy), several parameters can hit one and same harmonics. In this case, we have to use the linear combinations of these parameters instead of individual ones.
The universal program was written that can do all these things automatically. This program was applied to investigate the samples from the Hipparcos catalogue.
We illustrate the program by two samples for nearby (75-125 ps) and distant stars (300-500 ps) from the main sequence in H-R diagram. Also, the program was tested on artificial data1to show the effect in ideal case. The traditional solution using LST is shown in the table, too. The missed data in the table denote that the F-test (Broshe 1966) rejected the value in this cell.
This table shows that only the Sun motion can be detected certainly in the proper motions. The galactic rotation is polluted by unknown systematic motions which distort the 4th coefficient, though the Least Squares technique produces the solution that seems to be very reliable.
| Parameter | Simulation | 75 - 125 pc | 300 - 500 pc | |
| Vx | 2 | |||
| 10 | ||||
| LST | ||||
| Vy | 3 | |||
| 11 | ||||
| LST | ||||
| A | 8 | -- | ||
| 20 |
|
-- | -- | |
| LST | ||||
| B | 0 |
|
||
| 4 | ||||
| 16 | -- | -- | ||
| LST | ||||
The first attepmt of the method apllication for stellar kinematics was made in two papers by Vityazev & Tsvetkov (1989a, 1989b). The basic principles of our method are described in the paper by Vityazev (1994) who proposed to use the spherical functions to derive the mutual rotation between two reference frames. Our method is an extension of this approach for kinematics. It may be easily modified for many purposes if one wishes to test a model for correspondence to observational data.
Brosche P. 1966, Representation of Systematic Differences in Positions and Proper Motions of Stars by Spherical Harmonics, (Heidelberg: Veroff. Astr. Rechen-Inst), N17
Vityazev, V. V. & Tsvetkov, A. S. 1989a, Vestnik LGU, 1(2), 73
![]() , 1989b, Vestnik LGU, 1(2), 79
, 1989b, Vestnik LGU, 1(2), 79
Vityazev, V. V. 1994, Astron. and Astrop. Trans., 4, 195