Next: Scheduler, a distributed batch controller
Up: Data Processing Systems
Previous: Data Handling for PLANCK/LFI Ground Tests
Table of Contents -
Subject Index -
Author Index -
Search -
PS reprint -
PDF reprint
Pan, X. 2003, in ASP Conf. Ser., Vol. 314 Astronomical Data
Analysis Software and Systems XIII, eds. F. Ochsenbein, M. Allen, & D. Egret (San Francisco: ASP), 792
Phasor Algorithms of the SIM Fringe Estimation
Xiaopei Pan
Jet Propulsion Laboratory,California
Institute of Technology,4800 Oak Grove Drive, Pasadena, CA 91109
Abstract:
The Space Interferometry Mission (SIM) will provide unprecedented
micro-arcsecond (
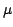
as) precision to search for extra-solar planets
and possible life in the universe. SIM will also revolutionize our
understanding of the dynamics and evolutions of the local universe
through hundred-fold improvements of inertial astrometry
measurements. SIM has two so-called guide interferometers to
provide stable inertial orientation knowledge of the baseline, and a science
interferometer to measure target fringes. The guide and science measurements
are based on the fringe phase measurements using a CCD detector. One of
SIM's key issues is to develop a new algorithm for calculation of fringe
parameters. Not only astrometric results need that new algorithm, but
also real-time fringe tracking requires a new method to calculate
phase and visibility fast and accurately. The formulas for the phasor
algorithms for fringe estimation are presented. The signal-noise ratio
performances of the fringe quadratures are demonstrated. The
advantages of phasor algorithms for application of fast fringe
tracking and on-board data compression are discussed.
A space-based astrometric interferometry mission, SIM, is a long
baseline optical interferometer optimized for global (inertial) and
narrow-angle (relative) astrometry. Global astrometry with accuracy of 4
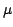 as permit trigonometric determination of distances throughout the
Galaxy. The narrow-angle astrometry at the level of 1
as permit trigonometric determination of distances throughout the
Galaxy. The narrow-angle astrometry at the level of 1 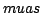 performs
definite searches for extra-solar planets (Bahcall 1991). The SIM is the only
astronomical instrument, that can unambiguously measure the masses of extra-solar
planets. The SIM instrument has two guide interferometers and a
science interferometer. The guide interferometers observe two bright
objects in order to provide an inertially stable baseline. Delay
measurements from guide stars are fed forward to the science
interferometer. Based on the knowledge of the baseline orientation in
space the science interferometer operates similar to the ground-based
Michelson interferometers (Shao 1988). The key to interferometer measurements is
the white light fringe determination. The SIM instrument uses path
length modulation implemented on the optical delay line for fringe
detection. All three interferometers in SIM use coherent fringe
demodulation and active fringe tracking. The 500 Hz modulation uses a
sawtooth waveform for 4 - 8 spectral channels simultaneously. The SIM
instrument has broad wavelength coverage from ultraviolet to
near-infrared. In order to reach high accuracy of fringe parameter measurements
it is important to develop new phasor algorithms.
performs
definite searches for extra-solar planets (Bahcall 1991). The SIM is the only
astronomical instrument, that can unambiguously measure the masses of extra-solar
planets. The SIM instrument has two guide interferometers and a
science interferometer. The guide interferometers observe two bright
objects in order to provide an inertially stable baseline. Delay
measurements from guide stars are fed forward to the science
interferometer. Based on the knowledge of the baseline orientation in
space the science interferometer operates similar to the ground-based
Michelson interferometers (Shao 1988). The key to interferometer measurements is
the white light fringe determination. The SIM instrument uses path
length modulation implemented on the optical delay line for fringe
detection. All three interferometers in SIM use coherent fringe
demodulation and active fringe tracking. The 500 Hz modulation uses a
sawtooth waveform for 4 - 8 spectral channels simultaneously. The SIM
instrument has broad wavelength coverage from ultraviolet to
near-infrared. In order to reach high accuracy of fringe parameter measurements
it is important to develop new phasor algorithms.
This paper presents formulas for fringe estimation based on the phasor algorithms,
and demonstrate the signal-noise ratio performances of the fringe quadratures.
The advantages of phasor algorithms for application of fast fringe tracking
and on-board data compression are discussed.
SIM is a fringe-scanning interferometer that needs to acquire and track
the white light fringe in order to equalize the paths of the two arms of the
interferometer at the nanometer level. The pathlength modulation implemented by
the voice coil uses a sawtooth waveform, and the detector is read out coherently
using eight time bins per scan.
The basic frame rate is 500 Hz, and each time bin is 0.125 ms. The
path length in one arm varies linearly with the stroke, which has a
length equal to the longest wavelength. Two guide-star
interferometers have 4 spectral channels, and a science interferometer
has 8 spectral channels. For all of spectral channels, one, or a
little more than one fringe, is scanned across CCD detectors.
The fringe irradiance is written as :
where N is the mean number of photons per scan, s is the stroke,
V is fringe visibility, k is the wave number (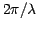 ),
and
),
and 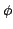 is the fringe phase. The modulation position
is the fringe phase. The modulation position
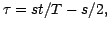 where t is time for a bin, and T is the time interval of a stroke.
where t is time for a bin, and T is the time interval of a stroke.
From the CCD measurements the accumulated photon counts for
each time bin can be written as :
The total photons per stroke are the summation of counts in all eight time bins:
For each channel we calculate the X and Y quadratures for the dithered signal.
In the simple case that the modulation amplitude matches a wavelength, i.e. 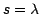 ,
we can combine the 8 bin data as follows:
,
we can combine the 8 bin data as follows:
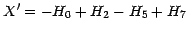 ,
,
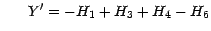 .
.
For most of channels the stroke is longer than their effective wavelengths.
We must define:
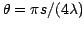 , where s is stroke,
, where s is stroke, 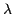 is wavelength;
is wavelength;
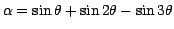 ,
,
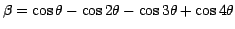 .
.
The true quadratures,
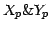 , i.e. X and Y phasor components, and
the total fluxes are calculated as :
, i.e. X and Y phasor components, and
the total fluxes are calculated as :
So the fringe visibility and phase are calculated as follows:
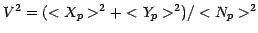 ;
;
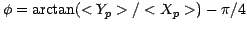 ,
,
where angle brackets 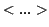 represent an average over certain
time periods of fringe tracking.
represent an average over certain
time periods of fringe tracking.
The photon counts of time bins obey Poisson distribution. The signal-noise ratio
of phasors can be expressed as
where 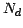 is the dark current, and
is the dark current, and 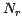 is the read noises.
is the read noises.
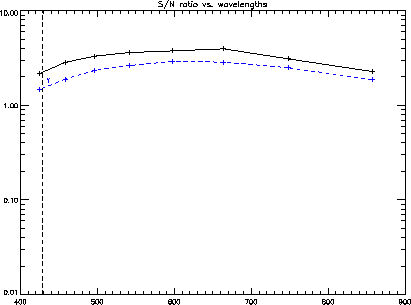
Simulations are conducted for a typical case of 30 seconds of
fringe tracking. For a 7th magnitude guide stars the signal-noise
ratios of X, Y phasors are shown in Figure 1. For
comparison, the signal-noise ratio of phasors in X and Y directions
are computed for the case of four time bins(Colavita 1999). It is shown that the
performances of signal-noise ratio drops significantly when the
wavelength of a spectral channel is shorter than the length of the
stroke. It is necessary to use new eight time bin algorithm
for uniform and improved performance.
Figure 1:
Signal-noise ratios of X, Y phasors
 |
This work developed new phasor algorithm and has been
successfully used for the MAM testbed experiments (Shaklan 1992). In order to keep
the paths of the two arms nearly equal, the MAM delay line must
acquire and track the white light fringe phase. Once the fringe
visibility calculated by the formulas above exceeds a threshold,
fringe tracking can start. By using the phase results from the
algorithm the system reports the absolute value of the fringe phase as
telemetry at the maximum rate that the fringe control loop runs(Hines
2002). For such real-time control system the phasor algorithm
has proven to be simple, fast and accurate.
Traditional non-linear fitting techniques, or the pseudo-inverse method are
much too slow, and are difficult to use for nanometer and millisecond
control. The phasor algorithm also can be used for the
on-board data processing in SIM. The data volumes that must be
down-loaded from the spacecraft to the ground station are extremely
high. Phasors computed by this algorithm can be used to compress
fringe data. It is important to maximize measurement
information while reducing data volume in SIM.
This paper presents the preliminary study of the phasor algorithm.
Cyclic errors, the vibration effects, and nonlinear strokes are a few
example of noises that will reduce the accuracy of fringe parameter
determination. Those issues need to be addressed in the near future.
This work was carried out at the Jet Propulsion Laboratory, California Institute
of Technology, under contract with the National Aeronautics and Space Administration.
References
Bahcall, J. 1991, The Decade of Discovery in Astronomy and Astrophysics, National Academy Press
Colavita, M. M. 1999, PASP, 111, 111
Shao, M. et al 1988, A&A,193,357
Shaklan, S. Colavita, M. M. & Shao, M. 1992, in ESO conf. and Workshop Proc. 39, 1271
Hines, B. 2002, Fringe Tracker Software Requirements, JPL reports
© Copyright 2004 Astronomical Society of the Pacific, 390 Ashton Avenue, San Francisco, California 94112, USA
Next: Scheduler, a distributed batch controller
Up: Data Processing Systems
Previous: Data Handling for PLANCK/LFI Ground Tests
Table of Contents -
Subject Index -
Author Index -
Search -
PS reprint -
PDF reprint
![]() , where s is stroke,
, where s is stroke, ![]() is wavelength;
is wavelength;
![]() ,
,
![]() .
.
![]() , i.e. X and Y phasor components, and
the total fluxes are calculated as :
, i.e. X and Y phasor components, and
the total fluxes are calculated as :
![]() ;
;
![]() ,
,
![]() represent an average over certain
time periods of fringe tracking.
represent an average over certain
time periods of fringe tracking.