Next: A Commodity Computing Cluster
Up: Data Analysis Tools, Techniques, and Software
Previous: MKRMF: Multi-Dimensional Redistribution Matrices
Table of Contents -
Subject Index -
Author Index -
PS reprint -
Bringer, M. & Boër, M. 2000, in ASP Conf. Ser., Vol. 216, Astronomical Data
Analysis Software and Systems IX, eds. N. Manset, C. Veillet, D. Crabtree (San Francisco: ASP), 640
An Automatic Astronomical Classifier Based on Topological Neural
Networks
M. Bringer, M. Boër
Centre d'Etudes Spatiales des Rayonnements (CESR/CNRS),
9 av du Colonel Roche,
31028 Toulouse cedex 04, France
Abstract:
We report progress in the development of an automatic classifier for
astronomical objects. The described method is adaptive. It is trained by
examples and doesn't need any training rules. The map is used later as a
code book by the
TAROT
(Télescope à Action Rapide pour les Objets Transitoires,
Rapid
Action Telescope for Transient Objects) data processing pipeline. It is
a general method which may be used for other purposes starting with
large surveys. In this paper, we describe the method, as well as the
results from test and general astronomical images taken by TAROT.
The setting up of new automatic observatories, essential in order to
understand rapid event such as gamma ray bursts, has shown the need to
develop fully automated software able to detect and classify sources in
a short time. There are now few good softwares able to detect and
measure sources even in crowded areas, but still resist the problem of
classification. The game consists of being able to attribute a nature to
every object detected on the frame, even though it is not a common
object. One of the solution may lie in the use of neural networks
(NN). Multilayers perceptron (Bertin & Arnouts 1996) and Self
Organizing Map (SOM)
(Mahonen & Hakala 1995) seem able to separate stars and galaxies. We
will at first expose the foundations of SOM in order to present our
Topological Neural Networks (TNN) that gives us our first good results
of classification.
It is quite difficult for a newcomer in the NN area to have a precise
idea of what is a NN. The definition proposed by Haykin (Haykin 1999) to
approach a NN as an adaptive machine is quite general:
A neural network is a massively parallel distributed processor made
up of simple processing units, which has a natural propensity for
storing experiential knowledge and making available for use.
A NN is just a group of connected units called neurons that perform useful computations through a process of learning.
The neuron is an information processing unit that is fundamental to the operation of NN. It can be modeled by Figure 1.
Figure 1:
Model of an artificial neuron.
 |
Where:
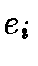 are the inputs,
are the inputs,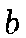 is the bias,
is the bias, is the activation function. Different functions are commonly in use. We have chosen the sigmoid function:
is the activation function. Different functions are commonly in use. We have chosen the sigmoid function:
Principles:
Neural Maps are a a group of connected neurons. From that point, we can
create lots of different NN depending on ordering of neurons, relations
between neurons and training inputs.
Multilayer Perceptron is characterized by the way neurons are linked to
each other. Typically, the input vector is connected to an input
layer. Each neuron of the input layer is connected to neurons of another
layer (which is called hidden layer if there are further layers), and so
on till the output layer. Neurons of a same layer are usually
independent one to each other. The connection between a neuron from a
layer to a neuron of another layer is done through a synaptic weight
which is used to store a knowledge. This knowledge is acquired thanks to
the learning process.
Topology of a TNN:
A TNN is a network that preserve the topology of inputs. In order terms,
two vectors close in the input space will be close in the output
space. This NN is a single layer network. The power of the network is
primaryly that neurons are dependant each other, in order to preserve the
topology, and secondly that the training process is done with no a
priori information on the inputs data.
We use 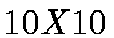 (dim p) neurons arranged in a two dimensional
array. Each neuron is associated with a weight vector
(dim p) neurons arranged in a two dimensional
array. Each neuron is associated with a weight vector 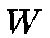 . In our case,
the input data consists of objects detected on the frame by our data
processing software TAITAR as a two-dimensional array of
. In our case,
the input data consists of objects detected on the frame by our data
processing software TAITAR as a two-dimensional array of 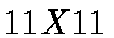 (dim
n) pixels. The network is presented on Figure 2.
(dim
n) pixels. The network is presented on Figure 2.
Figure 2:
Left: Configuration of a Topological Neural Network, Right: The
Topological Map after training.
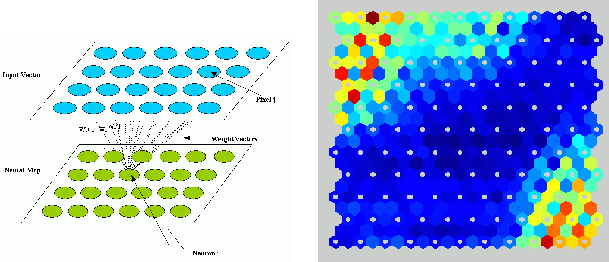 |
Before the training phase, initial values are given to the weight
vectors. We have adopted a linear initialization (Kohonen 1997) where the
weight vectors are initialized in an orderly fashion along the linear
subspace spanned by the two principal eigenvectors of the input data
used for the training procedure.
In each training step, the network will compute for every new input, 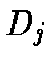 for each neurons:
for each neurons:
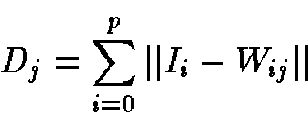 |
(1) |
We then select the Best Match Unit (BMU) and update the weight vectors of the map according to Equation 2.
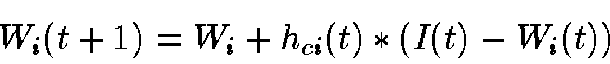 |
(2) |
where 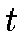 denotes the time and
denotes the time and 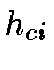 is the neighborhood kernel around the BMU.
is the neighborhood kernel around the BMU.
For every input data, the Network will compute for every neuron Equation 1.
The BMU will be the neuron 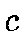 according to
according to
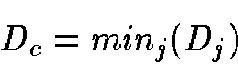 |
(3) |
This means that the weight vector of neuron 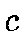 most closely resembles to the input vector
most closely resembles to the input vector 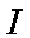 .
.
In order to preserve the topology of data, neurons are connected to
adjacent neurons by a neighborhood relation dictating the structure of
the map. The neighborhood kernel is an non-increasing function of time
and of the distance of unit 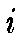 to the BMU. It defines the region of
influence that the input sample has on the map. In this work, we use the
Gaussian Kernel.
to the BMU. It defines the region of
influence that the input sample has on the map. In this work, we use the
Gaussian Kernel.
In order to train the net, we have used both simulated and original CCD
subframes of 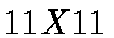 pixels containing either a point source, an
extended object, a blended object or a sky background. The images were
then mean subtracted and normalized to the unit length. Figure 2 shows
the result after training. We clearly see 3 different areas that
represent the point source area, the extended source area and the sky
background area. It is then possible to use the map in the TAROT
pipeline (Bringer et al. 2000). The idea is to calculate for every
objects detected as a subframe of
pixels containing either a point source, an
extended object, a blended object or a sky background. The images were
then mean subtracted and normalized to the unit length. Figure 2 shows
the result after training. We clearly see 3 different areas that
represent the point source area, the extended source area and the sky
background area. It is then possible to use the map in the TAROT
pipeline (Bringer et al. 2000). The idea is to calculate for every
objects detected as a subframe of 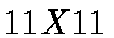 pixels, the BMU of the map. If
the BMU falls in the point source area, it means that our object is a
point source. If the BMU is a neuron on the frontier area, we can't give
more than a probability of being a point source.
pixels, the BMU of the map. If
the BMU falls in the point source area, it means that our object is a
point source. If the BMU is a neuron on the frontier area, we can't give
more than a probability of being a point source.
We have introduced a Topological Feature Map which is capable to learn
through experience and to discriminate between astronomical
objects. One of the particularity of the map is that we don't calculate
any parameters, and thus we do not introduce any subjective opinions
about the object. The input data are raw objects. We are now looking
forward to improving our map in order to deal with other types of
astronomical objects. One will have notice that the map doesn't show
any blended object area whereas we had some blended object in our
training data. We probably need fine tuning during the training phase
as well as a better training data set in order to classify the blended
object. When this map will be strengthen, we will try to consider the
temporal variability of objects. This is probably the next challenge of
astronomical classification.
References
Bringer, M. et al. 2000, this volume, 445
Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393
Haykin, S. 1999, in Prentice Hall International Editions, ISBN 0-13-908385-5
Kohonen, T. 1997, in Springer-Verlag Berlin Heidelberg New York Editions
Mahonen, P. H., & Hakala, P. J. 1995, ApJ, 452, 77
© Copyright 2000 Astronomical Society of the Pacific, 390 Ashton Avenue, San Francisco, California 94112, USA
Next: A Commodity Computing Cluster
Up: Data Analysis Tools, Techniques, and Software
Previous: MKRMF: Multi-Dimensional Redistribution Matrices
Table of Contents -
Subject Index -
Author Index -
PS reprint -
adass@cfht.hawaii.edu


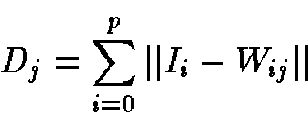
![]() denotes the time and
denotes the time and ![]() is the neighborhood kernel around the BMU.
is the neighborhood kernel around the BMU.