Next: Toolkit Based Extension of the SDSS Control System
Up: Telescope and Instrument Control Systems
Previous: An Effective PC/Linux Based Control System Upgrade for the UH 2.2-m Telescope
Table of Contents - Subject Index - Author Index - PS reprint - Yang, Y., Rees, N. P., & Chuter, T. 2000, in ASP Conf. Ser., Vol. 216, Astronomical Data Analysis Software and Systems IX, eds. N. Manset, C. Veillet, D. Crabtree (San Francisco: ASP), 279

Application of a Kalman Filter at UKIRT

Y. Yang, N. Rees, T. Chuter
Joint Astronomy Center, 660 N. Aohoku Place, University Park, Hilo, Hawaii, 96720

Abstract:

The tracking (i.e. unguided) performance of the United Kingdom Infra-Red Telescope (UKIRT) relies on the accuracy of its 24 bit absolute encoders. These have been long known to generate two systematic errors. The first is a periodic error resulting from the encoder deriving the last 8 resolution bits by interpolation between the $2^{16}$ rulings on its code disk. The error has exactly $2^{16}$ periods per revolution. The second error is quantization noise at the level of the $24^{th}$ bit.

A filter has been designed to reduce these effects and it has been inserted in the feedback loop of the telescope mount servo. Engineering tests and observers reports have noted a marked improvement in the telescope's tracking performance.

1. Introduction

UKIRT uses high resolution (24 bit) absolute shaft encoders to determine the telescope's orientation. These have been long known to have two systematic errors:

1. A periodic error resulting from the encoder deriving the last 8 resolution bits by interpolation between the $2^{16}$ rulings on its code disk. The error has exactly $2^{16}$ periods per revolution;
2. Quantization errors at the level of the 24th bit.

The first is the most noticeable and has a frequency of $2^{16}/86400\approx0.76$ Hz when tracking at sidereal rates. The amplitude of this error is about 0.7 arc-seconds peak to peak and has limited UKIRT's tracking (i.e. unguided) performance for many years.

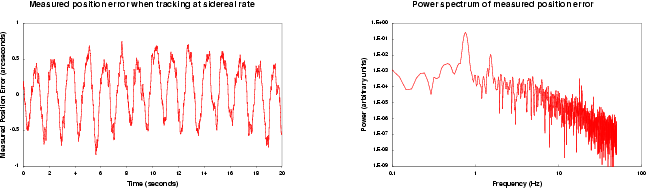
This error is shown by the two plots in Figure 1. The first is the measured position error when tracking at sidereal rates and it clearly shows the dominant sinusoidal error. The second is the power spectrum of the motion, which confirms the peak is at 0.76 Hz. There are a number of interesting aspects to the motion:

• It is from the encoder and not, for example, a structural resonance, because it has exactly the frequency of the encoder disk rulings and the frequency changes with the angular velocity of the telescope;
• There is a second harmonic at twice the fundamental frequency;
• It has been found, by experiment, that the error is phase stable over the entire UKIRT field of view.

Fortunately, the error is not seen whilst auto-guiding since the telescope servo uses the guide signals directly, thus bypassing the encoders. However, since UKIRT is an infra-red telescope it does observe fields where there are no visible guide stars since the visible light is heavily obscured by dust. At these times auto-guiding is not available and so the tracking performance is paramount.

Figure 1: The centroid motion and power spectra of a source at UKIRT before application of the results of this paper.

2. Encoder Design

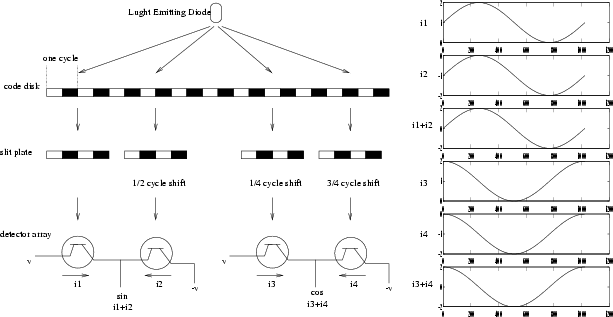
To understand the errors we must look at how the encoder produces a resolution of $2^{24}$ bits using a code disk with only $2^{16}$ rulings. This is illustrated in Figure 2. Light from an LED illuminates a code disc and slit plate, both of which have similar rulings but move relative to each other as the axis rotates. Light that passes through the code disk and slit plate is detected by photosensitive diodes. The slit plates are arranged in groups of four, with a $1/4$ period offset between each member of the group. The signals from the four detectors provide sine and cosine signals and they are combined using an arc-tangent multiplier. The result is digitized to give the additional 8 bits of resolution.

Figure 2: Principles of the 24 bit encoder fine track measurement (after Pearson, Kansky & Tobey 1990).

Minor imperfections in the encoder generate systematic errors in the measurement. For example, an error in the positioning of the slit plate will result in an approximately sinusoidal error with a period equal to the period of the code disk. These imperfections are the source of the periodic errors we observe.

3. Filter Design

In modeling the system we assume the measured position at sampling time $k$, say $Z_k$, can be represented by three terms, e.g.:

$$Z_k=X_k+Y_k+V_k,$$ (1)

where $X_k$ is the true telescope position, $Y_k$ is the systematic periodic measurement error and $V_k$ is a random measurement error, which includes the quantization error.

To estimate the measurement errors we introduce a periodic filter to model $Y_k$ and a Kalman filter to model $V_k$. The error estimates are then subtracted from the encoder reading in the encoder feedback path.

The periodic filter assumes the periodic errors are of the form:

$$Y_k=c_1sin(2^{16}X_k+\phi_1)+c_2sin(2^{17}X_k+\phi_2)$$ (2)

where $c_1$, $c_2$, $\phi_1$ and $\phi_2$ are determined by experiment. For the UKIRT hour angle encoder, $c_1$ and $c_2$ are $0.35$ and $0.012$ arcseconds respectively, whilst $\phi_1$ and $\phi_2$ are $4.95$ and $3.613$ radians. We have found these numbers to be remarkably stable which implies that the errors probably derive from a constant misalignment of the encoder slit plates.

The Kalman filter design is based on the assumption that $V_k$ is truly random with a Gaussian form and a standard deviation comparable to the size of the least significant bit of the encoder. This filter is primarily intended to reduce the quantization errors, but an unexpected side effect was that it significantly improved the performance of the periodic filter. The conclusion we drew was that the errors remaining after the periodic filter were fairly Gaussian and noise like and so were correctly rejected by the Kalman filter.

The final advantage of the filter is that it enabled us to increase the loop gain of the system by a factor of 2, thereby improving the frequency response in the presence of other disturbances.

4. Results

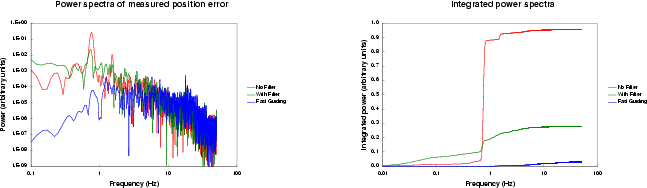
Since the encoder is the source of the errors, it cannot be used to determine the quality of the end result. Instead, we used position measurements made at 100 Hz on a bright star. We have done this in three modes:

• Tracking with the filter off,
• Tracking with the filter on, and
• Autoguiding with a tip-tilt secondary loop closed at 100 Hz.

The results are presented in Figure 3. The left figure is the traditional power spectra, and the right figure plots the total power integrated up to a particular frequency. Note that, whilst the fast guider gives clearly the best results, the effect of the periodic encoder error has been dramatically reduced when tracking. This is seen best in integrated power diagram since the power is on a linear, rather than a logarithmic, scale. The total power (i.e. the variance) of the centroid motion has been reduced by a factor of $\approx3$, and the power due to the periodic error no longer dominates the centroid motion.

Figure 3: Comparison of the power spectra of the source motion for three cases: no filter (which has the largest step and peak at 0.76 Hz); with filter (much reduced step and peak at 0.76 Hz); and for fast guiding (which has no 0.76 Hz feature since it does not use the telescope encoders).

5. Conclusion

A long term problem with UKIRT's tracking performance has been investigated and successfully solved. Whilst most observations do use the autoguider, this fix has been enormously successful at times when this proves impossible. For example, the ex Head of UKIRT (who should know!) penned the following words in a recent observers report:

``On Jupiter and Saturn we could not autoguide, but the much improved tracking (finally free from RA wobble) effectively has improved the angular resolution of our measurements on these planets by a factor of $\approx3$. This is a great improvement and we send our compliments to the team that finally accomplished this.''

What more can we say?

References

Pearson, E., Kansky, M., & Tobey, N. 1990, Presentation of 24 bit optical encoder system. unpublished material, BEI Motion Systems Company

© Copyright 2000 Astronomical Society of the Pacific, 390 Ashton Avenue, San Francisco, California 94112, USA Next: Toolkit Based Extension of the SDSS Control System
Up: Telescope and Instrument Control Systems
Previous: An Effective PC/Linux Based Control System Upgrade for the UH 2.2-m Telescope
Table of Contents - Subject Index - Author Index - PS reprint -