Applying the standard weighted mean formula,
![$
[\sum_i {n_i \sigma^{-2}_i}]
/
\break
[\sum_i {\sigma^{-2}_i}]
$](img1.gif)
,
to determine the weighted mean
of data,
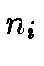
, drawn from a Poisson distribution, will,
on average,
underestimate the true mean by
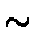
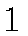
for all true mean
values larger than
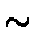
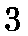
when the common assumption is made
that the error of the
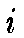
th observation is
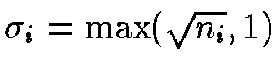
.
This small, but statistically significant offset,
explains the long-known observation that chi-square minimization techniques
using the modified Neyman's
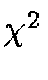
statistic,
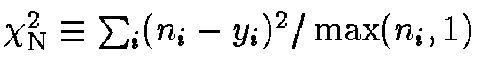
,
to analyze Poisson-distributed data will
typically predict a total number of counts that
underestimates the true total
by about
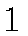
count per bin.
Based on my finding that the weighted mean of data
drawn from a Poisson distribution can be
determined using the formula
^{-1}
]
/
[
\sum_i (n_i+1)^{-1}
]
$](img10.gif)
, I have proposed a new
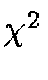
statistic,
![$\chi^2_\gamma
\equiv
\sum_i
[ n_i + \min( n_i, 1) - y_i ]^2
/
[ n_i + 1 ]$](img11.gif)
,
should always be used to analyze Poisson-distributed data
in preference to the modified Neyman's
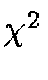
statistic
(Mighell 1999, ApJ, 518, 380).
I demonstrated the power and usefulness of

minimization
by using two statistical fitting techniques and three
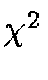
statistics
to analyze simulated X-ray power-law 15-channel spectra
with large and small counts per bin.
I showed that

minimization with
the Levenberg-Marquardt or Powell's method can produce
excellent results (mean errors
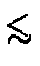
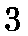
%)
with spectra having as few as 25 total counts.