| (1) |
There are now several methods available for reconstructing a ``super image" of the sky from a set of such dithered images. The different algorithms, including the ``Drizzling" method developed by the authors, the method proposed recently by Tod Lauer, and more conventional approaches based on image interpolation will be compared and contrasted and examples of their use on real data given.
Finally some comments about future developments, both of cameras and algorithms will be made.
Many detectors in astronomy have pixels which are too large to adequately sample the point-spread function of the image falling on them. Camera design is always a compromise and larger pixels give a larger field for a given number of pixels and have other advantages. Under-sampled cameras are common and a famous example is the Wide Field Planetary Camera 2 (WFPC2) on the Hubble Space Telescope.
The dithering and undersampling of astronomical cameras together pose important problems of observation planning, execution and subsequent data reduction. This paper introduces the subject and describes several methods for the combination of such data. Particular emphasis is given to the processing of data from the optical and near-IR cameras on the Hubble Space Telescope (HST). We first describe how the optics, detector and dithering affect the resultant image. The bulk of the paper is a discussion of several different image reconstruction methods and their relative merits. Some concluding remarks about the effects of the pixel-response function are also included. A practical rather than theoretical approach to these problems is adopted.
Dithering is not always the optimum strategy. Executing the dithers with adequate accuracy (at a sub-pixel level) may be difficult or impose overheads. Splitting exposures may lead to additional noise (e.g., readout noise in cases where the images are detector rather than sky noise limited) and dithering inevitably leads to a smaller final field of the deepest imaging. Finally the precise measurement of shifts between images and the reconstruction of the final co-added image can be time consuming.
| (1) |
where ![]() is the convolution operator and
is the convolution operator and ![]() are indices over
a fine grid which well-samples the images.
are indices over
a fine grid which well-samples the images.
![]() is then sampled at the pixel centres of the final output detector.
This sampling may be regarded as
a further multiplication with a two-dimensional grid of
is then sampled at the pixel centres of the final output detector.
This sampling may be regarded as
a further multiplication with a two-dimensional grid of ![]() -functions
(a Shah function).
-functions
(a Shah function).
For an undersampled camera system the separation of the sampling points
is normally the same as the width of the pixel and hence the extent of the
PRF but this need not always be the case. It is important to note that in
typical examples such as the WFC channels of WFPC2 the convolution with
the PRF (approximately a square ``box'' of width ![]() ) causes a loss
of high spatial frequency information which is greater than
that due to the convolution with the PSF (an Airy function with FWHM of
about
) causes a loss
of high spatial frequency information which is greater than
that due to the convolution with the PSF (an Airy function with FWHM of
about ![]() at 500nm).
at 500nm).
 |
When multiple dithered images are taken with an adequate number of
sub-pixel offsets the sampling of the
intensity distribution ![]() is improved and, in principle, should allow
a full reconstruction. This is the aim of most of the methods discussed
below. No amount of dithering can compensate for the loss of information
introduced by the convolution with the PRF but we can hope to combine a
set of well-dithered images resembling that on the right in Figure 1 to
produce a result similar to that at the centre.
is improved and, in principle, should allow
a full reconstruction. This is the aim of most of the methods discussed
below. No amount of dithering can compensate for the loss of information
introduced by the convolution with the PRF but we can hope to combine a
set of well-dithered images resembling that on the right in Figure 1 to
produce a result similar to that at the centre.
Another simple approach is to shift each image to bring them into alignment and then coadd the results. The coaddition can then reject anomalous values such as cosmic rays or hot pixels. This may be done either using simple ``shift-and-add'' or a more sophisticated interpolation method. For well-sampled data and a careful choice of interpolator (e.g., sinc) this technique can work very well and is often used on ground-based images. Fully developed software for these tasks exists and is widely used (e.g., imcombine in IRAF and its variants in other packages). Unfortunately this is not true of undersampled data which, when interpolated, will inevitably suffer from artifacts and smoothing which will also have the side-effect of smearing small image defects such as cosmic rays and hence making their detection and suppression less effective. Shift-and-add normally involves replacing each pixel from the input image by a square of the same size before the ``shift'' stage and hence involves an additional convolution with the PRF and corresponding degradation of resolution. Some implementations of these methods also cannot handle geometrical distortion corrections or arbitrary rotations or scale changes. In general it is also not possible to give each input pixel its own weighting.
Drizzling is a ``forward'' method unlike typical interpolation methods. Each pixel of the input images is ``shrunk'' by a user-specified amount (known as the pixfrac) and the corners of this smaller square are transformed onto the output pixel grid using knowledge of the geometrical distortion and any shift, rotation and scale specified. The overlap of this quadrilateral with the pixels of the output is calculated and the data values are combined using an optimal weighting scheme in which the input weight depends on the weight assigned to the input pixel as well as the size of the overlap with the output pixel under consideration. The method is illustrated in Figure 2.
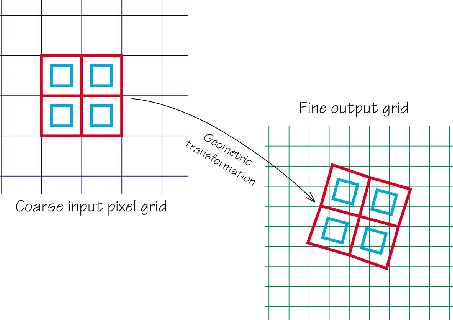 |
Drizzling, although conceptually very simple, is fast and flexible. Large
images, mosaicing, arbitrary geometrical distortions can be easily handled.
Input pixels can be individually weighted and these weights are optimally
combined and propagated to a separate output weight image. The noise
characteristics
of the resultant output images are understood and simple formulae are
available which give the ratio of the noise of a drizzled output image
to the case of no noise correlation. This information is very valuable if
the drizzled output images are to be passed to object detection and
classification software such as SExtractor (Bertin & Arnouts 1996) which
needs an
estimate of the noise. The average FWHM of a point-source in an
output drizzled image may be estimated by adding in quadrature the width
of the incident optical PSF, the width of the PRF and the pixfrac when
all three quantities are expressed in the same units. This rule-of-thumb
predicts a FWHM of ![]() pixels for the case of the HST/WFC/F606W HDF-S combined
images (which have
pixels for the case of the HST/WFC/F606W HDF-S combined
images (which have ![]() " pixels) in close agreement with the
measured width of (the rare) stars in this image.
" pixels) in close agreement with the
measured width of (the rare) stars in this image.
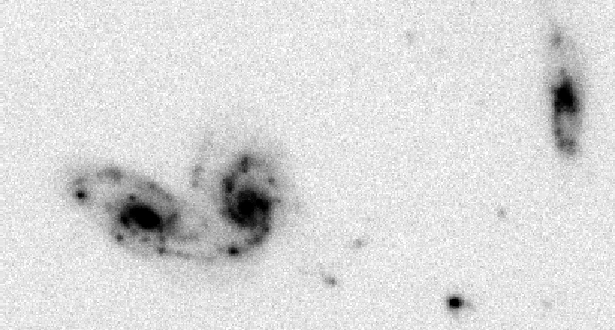
There is a widely used drizzle implementation in IRAF. It has become the standard method for the combination of dithered HST imaging data and has also been used for other data (e.g., ISOCAM, ESO Imaging Survey). An example of the application of drizzling to the deepest optical image of the sky yet taken (Gardner et al. 2000) is shown in Figure 4. This is a combination of 193 unfiltered STIS CCD images with a total exposure time of 155ks. The large number of images resulted in comprehensive sub-pixel sampling and allowed a combination which was equivalent to ``interlacing''.
The implementation of drizzling using the scheme shown in Figure 2 is just one possibility. Different kernels for distributing weight on the output grid could be used and might have advantages for some applications. Gilliland et al. (1999) have used a method of their own which is similar to classic drizzling but uses a Gaussian kernel. This and other options will be included in a future release of drizzle.
On the other hand drizzling may be criticised in various ways: the choice of the pixfrac parameter is somewhat arbitrary; there is a small amount of space-variant smoothing of the output image causing noise-correlations on small scales; the effective interpolation scheme applied is a variant of linear interpolation results in some aliasing. Finally, as with all linear reconstruction methods, drizzling makes no attempt to reduce the loss of resolution resulting from the convolution with either the PSF or the PRF.
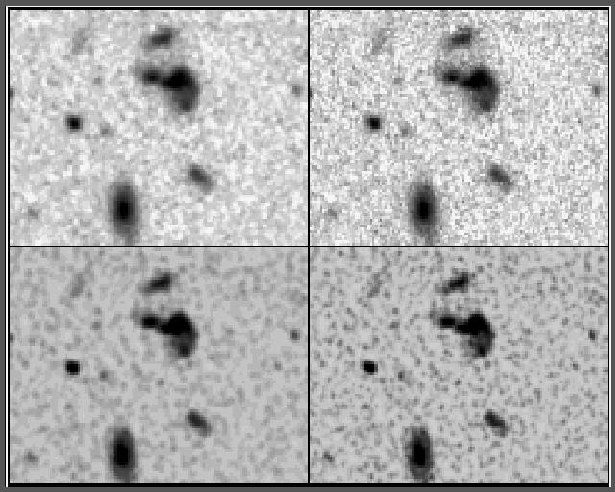
The actual combination of the images is only part of the processing of dithered data sets. It is also necessary to measure the shifts between frames accurately as well as detect and flag artifacts so that they do not contribute to the output image. This is particularly difficult when all the data frames have different pointings and it is not possible to detect artifacts using conventional methods. A package of tools for handling dithered HST data is available as the dither package in STSDAS (Fruchter et al. 1997). It has also proved possible to use drizzling along with other tools to register such images, detect and flag bad pixels in the input images and then do an optimal combination. Figure 3 gives an example of the application of this technique. Gonzaga et al. (1998) have compiled a ``cookbook'' where comprehensive worked examples of applying the dither package to a variety of realistic datasets are presented.
 |
 |
Tod Lauer (1999a) has recently looked at the problem of combining dithered undersampled images in a fresh way with the aim of avoiding some of the problems of the methods discussed so far. The aim was reconstruction of a ``super-image'' which is Nyquist sampled without the small and space varying blurring which is inevitable in methods such as drizzling. His method works in Fourier space and follows from earlier work on one-dimensional sampled data by Bracewell (1978).
The Fourier transform of an undersampled dataset is periodic with the ``satellites'' overlapping each other. This overlap is the cause of aliasing and leads to artifacts in data space. However, when multiple dithered input images are available a linear combination of the Fourier transforms may be derived in which the aliasing is suppressed and the Fourier transform of a critically sampled ``super-image'' computed.
This method is probably the best currently available for reconstructing fine scale detail of a small region of the sky free of aliasing artifacts in the case of well-dithered data sets. Because the combination is done in Fourier space it is very difficult to include geometric distortion correction and flexible pixel weighting. It is proposed that these steps can be separated from combination itself and done as pre or post-processing. Unfortunately there is no current common-user implementation which limits its current applicability.
 |
This effect can be mapped directly if many dithered exposures of the same
field are available. An example of this is given in Figure 6 for the case of
the NICMOS observations of the Hubble Deep Field South. Alternatively the
effect of the PRF on photometry may be deduced by reconstructing the
convolution of the PSF and PRF using Lauer's method and then moving
a sampling grid of ![]() -functions and summing up to obtain a two-dimensional
map of the measured response of a point-source at different sub-pixel
positions. Applications of these methods to the WFPC2 and Camera 3 of NICMOS
are described in Storrs et al. (1999) and Lauer (1999b) where more
details and suggested schemes for correcting this effect are presented.
-functions and summing up to obtain a two-dimensional
map of the measured response of a point-source at different sub-pixel
positions. Applications of these methods to the WFPC2 and Camera 3 of NICMOS
are described in Storrs et al. (1999) and Lauer (1999b) where more
details and suggested schemes for correcting this effect are presented.
 |
Adorf, H.-M., & Hook, R. 1995, ``High resolution images from multiple `dithered' frames", in: Proc. ST-ECF workshop on ``Calibrating and understanding HST and ESO instruments", (Garching: European Southern Observatory), 251
Bertin, E. & Arnouts, S. 1996, A&AS, 117, 393
Bracewell, R. N. 1978, ``The Fourier Transform and Its Applications'' (New York: McGraw-Hill)
Devillard, N., 1999, ``Infrared Jitter Imaging Data Reduction: Algorithms and Implementation'', in ASP Conf. Ser., Vol. 172, Astronomical Data Analysis Software and Systems VIII, ed. D. M. Mehringer, R. L. Plante, & D. A. Roberts (San Francisco: ASP), 333
Fruchter, A. S., & Hook, R. N. 1997, ``A novel image reconstruction method applied to deep Hubble Space Telescope Images", Invited paper, in Applications of Digital Image Processing XX, ed. A. Tescher, Proc. S.P.I.E. vol. 3164, 120
Fruchter, A. S., Hook, R. N., Busko, I. C., & Mutchler, M. 1997,``A Package for the Reduction of Dithered Undersampled Images'', in proceedings of the 1997 HST Calibration Workshop, eds. Stefano Casertano, Robert Jedrzejewski, Charles D. Keyes, and Mark Stevens, (Baltimore: STScI), 518
Fruchter, A. S., & Hook, R. N. 1998, ``A Method for the Linear Reconstruction of Undersampled Images", astro-ph/9808087, submitted to PASP
Gardner J. P., Baum, S. A., Brown T. M., Carollo, C. M., Christensen, J., Dashevsky I., Dickinson M. E., Espey B. R., Ferguson H. C., Fruchter A. S., Gonnella A. M., Gonzalez-Lopezlira R. A., Hook R. N., Kaiser M. E., Martin C. L., Sahu K. C., Savaglio, S., Smith T. E., Teplitz H. I., Williams R. E., & Wilson, J. 2000, ``The Hubble Deep Field South - STIS Imaging", AJ, in press
Gilliland, R. L., Nugent, P. E., & Phillips, M. M. 1999, ``High-Redshift Supernovae in the Hubble Deep Field'', ApJ, 521, 30
Gonzaga, S. et al. 1998, ``The Drizzling Cookbook'', STScI Instrument Science Report WFPC2 98-04
Hook, R. N., & Adorf, H.-M. 1995, ``Methods for combining `dithered' WFPC-2 images", in: Proc. Calibrating Hubble Space Telescope: Post Servicing Mission, Baltimore, MD, Space Telescope Science Institute, 341
Lauer, T. R. 1999a, ``Combining Undersampled Dithered Images", PASP, 111, 227
Lauer, T. R. 1999b, ``The Photometry of Undersampled Point Spread Functions'', PASP, 111, 1434
Storrs, A., Hook, R., Stiavelli, M., Hanley, C. & Freudling, W. 1999, ``Camera 3 Intrapixel Sensitivity", STScI Instrument Science Report NICMOS-99-005
Williams, R. E., Blacker, B., Dickinson, M., Dixon, W. V., Ferguson, H. C., Fruchter, A. S., Giavalisco, M., Gilliland, R., Heyer, I., Lucas, R. A., McElroy, D. B., Petro, L., Postman, M., Adorf, H-.M., & Hook, R. N. 1996, ``The Hubble Deep Field: Observations, Data Reduction, and Galaxy Photometry", AJ,112, 1335.