Object Classification as a Data Analysis Tool

Object classification methods can be a valuable data analysis tool for large, multi-parameter data sets. This paper reviews the steps to create a classifier and the various training methods available, and it discusses some astronomical applications of classifiers.

1. Introduction

Modern astronomers are awash in a sea of data. It can be difficult to understand large data sets using standard data analysis tools. The problem is particularly acute for data sets sets containing many objects, with many measured properties for each object. The typical approaches of plotting one parameter against another, computing histograms, measuring correlations, and so on are simply insufficient for exploring the data when there are more than a handful of parameters for each object in the sample.

Object classification methods are very useful tools for data exploration in large, complex problems. Such tools have traditionally been described as artificial intelligence methods, which may account for some of the skepticism among astronomers as to the applicability of these methods to quantitative analysis. However, in this paper I argue that these methods can be an invaluable tool for data analysis of large data sets. Classifiers need not be seen as mysterious black boxes that just spit out the answers; decision trees, in particular, represent a relatively simple geometric partitioning of the parameter space that can provide an accurate, understandable characterization of a complex data set.

In this paper I define in general terms what object classification is (§2) and the steps required to construct a classifier (§3); I give an overview of classification methods along with the arguments in favor of my preferred decision tree methods (§4); and I discuss some astronomical applications of classifiers from my own work (§5). The final section (§6) summarizes the results.

2. What is Classification?

A classifier is an algorithm that takes a set of parameters (or features) that characterize objects (or instances) and uses them to determine the type (or class) of each object. The classic example in astronomy is distinguishing stars from galaxies. For each object, one measures a number of properties (brightness, size, ellipticity, etc.); the classifier then uses these properties to determine whether each object is a star or a galaxy. Classifiers need not give simple yes/no answers -- they can also give an estimate of the probability that an object belongs to each of the candidate classes.

Generally the computationally hard part of classification is inducing a classifier, i.e., determining the optimal (or at least good) values of whatever parameters the classifier will use. I consider here only methods for supervised classification, meaning that a human expert both has determined into what classes an object may be categorized and also has provided a set of sample objects with known classes. This set of known objects is called the training set because it is used by the classification programs to learn how to classify objects. There are also unsupervised classification methods in which the induction engine works directly from the data, and there are neither training sets nor pre-determined classes.

In the training phase, the training set is used to decide how the parameters ought to be weighted and combined in order to separate the various classes of objects. In the application phase, the weights determined in the training set are applied to a set of objects that do not have known classes in order to determine what their classes are likely to be.

3. Steps in Developing a Classifier

Create a training set -- A training set contains a list of objects with known classifications. Ideally the training set should contain many examples (often thousands of objects) so that it includes both common and rare types of objects. The training set should be accurately classified, and it should be a representative sample. Both of these goals can be hard to achieve. For example, in star/galaxy classification, it is difficult to determine accurate classifications by eye for fainter objects, and human-constructed training sets often have a brightness distribution that is heavily biased toward bright objects. In this case, we can construct much more accurate training sets using deep CCD observations to determine the true classification for a large set of objects. When possible, acquiring higher quality ``truth'' data for the training set is a highly desirable approach.

Select powerful features -- The choice of features to measure for each object is crucial in determining the ultimate accuracy of the classifier. Ideally the features should be relevant to the classification, independent, and powerful in separating the different classes.

Adding irrelevant parameters (which effectively are random variables uncorrelated with the classes of the objects) makes training harder. Training classifiers is an optimization problem in a many-dimensional space. Increasing the dimensionality of the space by adding more parameters makes the optimization exponentially more difficult. It is always better to give the algorithm only relevant parameters than to expect it to ignore irrelevant parameters.

Do not ask the classifier to rediscover everything you already know about the data. Parameters should be combined when possible to produce more powerful features. For example, if the image shapes of some class of object are similar, include a brightness-independent shape parameter rather than simply giving the classifier raw pixel values.

A useful approach to identifying the best parameters is to train many times on subsets of the features. This has proven an effective way to prune unnecessary parameters (Salzberg et al. 1995). Another useful approach is to examine the weights assigned to the various features by the classifier. Important features are given a high weight, while unimportant features may not be used at all. With some methods (e.g., neural nets) this is not practical, but the decision tree methods lend themselves to this sort of analysis.

Train the classifier -- The choice of an algorithm for classification is in many ways the easiest part of developing a scheme for object classification. The discussion below (§4) indicates that there are several ``off-the-shelf'' approaches available (though there is obviously still room for improvement.) Typically this is a fairly mechanical process: put the training set into a form acceptable by the induction program, run the program, and convert the program's output into a form suitable for use in your classification procedure.

There has been a great deal of research recently on methods for combining multiple classifiers to produce more accurate classifications, e.g., bagging (Breiman 1996) and boosting (Freund & Schapire 1996). I am currently exploring the utility of these methods for astronomical applications and routinely use voting classifiers in my own work.

Assess classifier accuracy -- Once a potentially useful classifier has been constructed, the accuracy of the classifier must be measured. Knowledge of the accuracy is necessary both in the application of the classifier and also in comparison of different classifiers.

The accuracy can be determined by applying the classifier to an independent training set of objects with known classifications. This is sometimes trickier than it sounds. Since training sets are usually difficult to assemble, one rarely has the resources to construct yet another set of objects with known classifications purely for testing. One must avoid the temptation to train and test on the same set of objects, though; once an object has been used for training, any test using it is necessarily biased.

I normally use five-fold cross-validation to measure the classifier accuracy. The training set is divided into five randomly selected, roughly equal-sized subsets. The training is repeated five times, excluding a single subset each time, with the resulting classifier tested on the excluded subset. The advantage of cross-validation is that all objects in the training set get used both as test objects and as training objects. This ensures that both rare and common types of objects are used in testing. The training process must be repeated many times (especially if voting classifiers are used), but in most applications the necessary computer time is more readily available than is the human expert time required to generate independent test and training sets.

4. Classification Methods

The classification problem becomes very hard when there are many parameters. There are so many different combinations of parameters that techniques based on exhaustive searches of the parameter space are computationally infeasible. Practical methods for classification always involve a heuristic approach intended to find a ``good-enough'' solution to the optimization problem.

4.1. Neural Networks

Neural networks are probably the most widely known classification method. The biggest advantage of neural networks is that they are general: they can handle problems with many parameters, and they can work well even when the distribution of objects in the

-dimensional parameter space is very complex. The major disadvantage of neural networks is that they are slow, especially in the training phase but also in the application phase. Another significant disadvantage is that it is very difficult to determine how the net is making its decision. Consequently, it is hard to determine which of the image features being used are useful for classification and which are worthless. As discussed above (§3.2), the choice of the best features is an important part of developing a good classifier, and neural nets do not give much help in this process.

4.2. Nearest-Neighbor Classifiers

For the nearest-neighbor approach, one simply finds in the

-dimensional feature space the closest object from the training set to the object being classified. Since the neighbor is nearby, it is likely to be similar to the object being classified and so is likely to be the same class as that object. Nearest neighbor methods can give good results if the features are chosen carefully, but they have several disadvantages. They do not simplify the distribution of objects in parameter space to a comprehensible set of parameters. Instead, the training set is retained in its entirety as a description of the object distribution. (There are some thinning methods that can be used on the training set, but the result still does not usually constitute a compact description of the object distribution.) The method is also rather slow if the training set has many examples. Most seriously, nearest-neighbor methods are very sensitive to the presence of irrelevant parameters. Adding a single parameter that has a random value for all objects (so that it does not separate the classes) can cause these methods to fail miserably.

4.3. Axis-Parallel Decision Trees

In axis-parallel decision tree methods¹, a binary tree is constructed in which at each node a single parameter is compared to some constant. If the feature value is greater than the threshold, the right branch of the tree is taken; if the value is smaller, the left branch is followed. After a series of these tests, one reaches a leaf node of the tree where all the objects are labeled as belonging to a particular class.

There is a simple geometric picture of a decision tree: the parameter space is partitioned with a set of hyperplanes into separate volumes, with each volume labeled according to the classes of objects found within it. The hyperplanes are arranged in a tree structure for convenience and efficiency in determining into which partition an object falls. Trees based on using only a single parameter for each test are called axis-parallel because they partition the parameter space with a set of hyperplanes that are parallel to all of the feature axes except for the one being tested.

Axis-parallel decision trees are usually much faster in the training phase than neural network methods, and they also tend to be faster during the application phase. Their disadvantage is that they do not adapt as well to complex distributions. In fact, even simple shapes can cause these methods difficulties. For example, consider a simple 2-parameter, 2-class distribution of points with parameters

that are all of type 1 when

and are of type 2 when

(Figure 1). To classify these objects with an axis-parallel tree, the straight diagonal line that separates the classes is approximated by a series of stair-steps. Consequently, axis-parallel trees tend to be rather elaborate for realistic problems; it is not uncommon for them to require hundreds of nodes.

**Figure 1:** Sample classification problem with only two features. *Solid line*: oblique decision tree. *Dashed line*: axis-parallel decision tree. The true dividing line for the simulated data is the square's diagonal. The oblique decision tree is both simpler and more accurate than the axis-parallel tree.
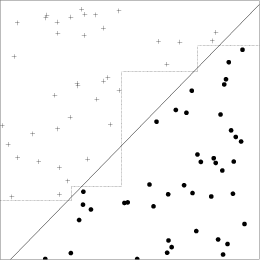$\begin{figure} \epsfxsize=0.4\textwidth \centerline {\epsfbox{O6-01-1.eps}}\end{figure}$

4.4. Oblique Decision Trees

Oblique decision trees attempt to overcome the disadvantage of axis-parallel trees by allowing the hyperplanes at each node of the tree to have any orientation in parameter space (Heath, Kasif, & Salzberg 1993; Murthy, Kasif & Salzberg 1994). Mathematically, this means that at each node a linear combination of some or all of the parameters is computed (using a set of feature weights specific to that node) and the sum is compared with a constant. The subsequent branching until a leaf node is reached is just like that used for axis-parallel trees.

Oblique decision trees are considerably more difficult to construct than axis-parallel trees because there are so many more possible planes to consider at each tree node. As a result the training process is slower. However, they are still usually much faster to construct than neural networks. They have one major advantage over all the other methods: they often produce very simple structures that use only a few parameters to classify the objects. It is straightforward through examination of an oblique decision tree to determine which parameters were most important in helping to classify the objects and which were not used.

Most of our work has concentrated on oblique decision trees using the freely available software OC1²(Murthy, Kasif, & Salzberg 1994), though we have used all the methods mentioned above. Oblique decision trees represent a good compromise between the demands of computational efficiency, classification accuracy, and analytical value of the results.

5. Astronomical Applications of Classifiers

5.1. Star-Galaxy Classification for the Guide Star Catalog-II

**Figure 2:** 530 $\times$ 300 pixel (8.8 $\times$ 5 arcmin) section of digitized Palomar Sky Survey II plate. Objects brighter than from Postman's deep CCD images are marked (squares are stars, circles are galaxies.) Our goal is to develop a classification algorithm that can distinguish the stars from the galaxies (which is hard for faint objects).
$\begin{figure} \epsfxsize=0.7\textwidth \centerline {\epsfbox{O6-01-2.eps}}\end{figure}$

The Guide Star Catalog-II is now under construction at the Space Telescope Science Institute (Lasker et al. 1995). It will have nearly one billion objects and will be based on digitized photographic data taken in a variety of colors and at several different epochs, so it will include both color and information on proper motions of objects in the catalog. This project needs an accurate, automatic star-galaxy classifier (Figure 2).

The inhomogeneity of the GSC-II data makes developing a classifier devilishly difficult. There is a considerable variation in the characteristics of images from different photographic plates. The sky brightness and atmospheric seeing change with time. The telescope optical characteristics also cause a slow variation in these parameters from the center to the edges of the plates. The atmosphere causes the images of objects photographed directly overhead (at the zenith) to differ from images of the same objects photographed near the horizon. Finally, the photographic plates are variably non-linear in their response to light. All of these factors combine to make the image features of identical objects appear to change from one plate to another.

**Figure 3:** Total density versus peak density for stars (dots) and galaxies (plusses) measured on GSC-II photographic plates. (a) The distribution for a single plate (XJ262) is well-defined. (b) The distribution for five plates differs for different plates.
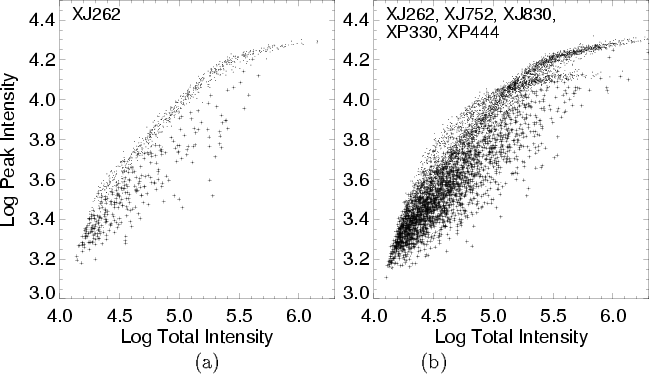$\begin{figure} \epsfxsize=\textwidth \epsfbox{O6-01-3.eps} \centerline {\hfill (a) \hfill (b) \hfill}\end{figure}$

Image parameters that separate stars and galaxies for a single GSC-II plate are readily found (Figure 3a). Stars and galaxies for this training set were identified using a deep CCD catalog (Postman et al. 1996). The distribution is non-linear as a result of the non-linear response of the photographic plate to light, but otherwise a reasonably simple and accurate classifier can be constructed using only these two parameters. However, the problem gets very messy when one compares objects from different plates (Figure 3b). The well-defined distributions for individual plates can be discerned here, but it would be practically impossible to develop an accurate classifier based on these parameters.

The straightforward solution to this problem is to generate many training sets to cover all the possible variations in object parameters. That is not a viable approach for the GSC-II project, because we have many thousands of photographic plates. Both the human expense of generating training sets and the computational expense of retraining the classifier on each plate are prohibitive.

We are instead using a novel approach for scaling these parameters so that they are plate-independent. Rather than using the raw values of the parameters, we use the ranks of the parameters (see White 1997 for the details.) The ranks are computed separately for objects from each plate. Once converted to ranks, the features for all objects can be combined and a single classifier can be used for objects from different plates (Figure 4).

**Figure 4:** (a) Distribution for objects from Figure 3(b) after transformation using ranks. Stars and galaxies from different plates separate very well. (b) Error rate (at high galactic latitude) as a function of magnitude for an oblique decision tree based on parameters transformed using ranks. Very good accuracy is achieved for brighter objects, and even for faint objects the accuracy is good.
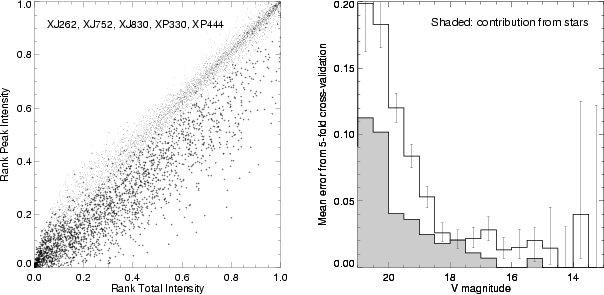$\begin{figure} \plottwo{O6-01-4a.eps}{O6-01-4b.eps} \end{figure}$

5.2. The FIRST Bright Quasar Survey

The FIRST survey is a radio sky survey planned to cover 10,000 square degrees of the northern sky with the VLA at a resolution of 5$^$ and with a source detection limit of 1 mJy, both of which are great improvements over previous radio surveys (Becker, White, & Helfand 1995; White, Becker, Helfand, & Gregg 1997). The FIRST catalogs and images released to date cover about 6000 deg

and contain about 550,000 sources. See the FIRST web pages (http://sundog.stsci.edu) for more information and access to the data.

We are engaged in a large quasar survey using a sample defined by coincidences between FIRST radio sources and stellar optical counterparts from the APM catalog. The FIRST Bright Quasar Survey (FBQS; Gregg et al. 1996, White et al. 2000) is complete to magnitude R=17.8 over 2680 deg

and includes 636 quasars. To define the FBQS sample, we set various (conservative) limits on the radio-optical position difference ( $<1.2\arcsec$ ), the optical morphology (stellar on at least one POSS-I plate), and the optical color (

, i.e., not too red). This defined a candidate list of 1238 objects; to date we have obtained spectra of 1130, with 56% being confirmed as quasars. The other objects are BL Lacs, narrow-line AGN, star-forming H II region galaxies, optically passive galaxies, and stars.

In our most recent paper (White et al. 2000), we considered the question of how efficiently quasars can be selected. With our current criteria, 44% of the candidates turn out to be non-quasars. Before obtaining spectra we already have a good deal of information about the candidates: radio fluxes and morphology, optical brightness, color, and morphology, etc. Can this information be used to eliminate some of the non-quasar candidates from our observing program, thus saving telescope time?

**Figure 5:** (a) Distribution of the *a priori* probability that an object is a quasar, , for all identified FBQS candidates. The shaded histogram is the distribution of confirmed quasars, while the unshaded area represents non-quasars. A perfect classifier would put all the quasars at and all the non-quasars at . (b) Completeness and reliability of the sample as a function of the threshold selected for the probability . The completeness is the fraction of quasars from the complete FBQS sample that are included at the selected threshold; the reliability is the fraction of selected candidates that are quasars.
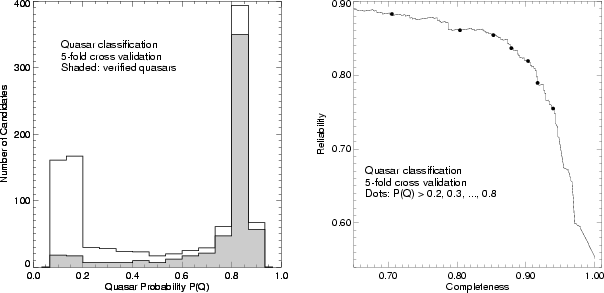$\begin{figure} \plottwo{O6-01-5a.eps}{O6-01-5b.eps} \end{figure}$

We used the spectral classifications of $\sim1000$ objects to create a training set for the oblique decision tree classifier. Using weighted, voting, decision trees, the sample reliability can be substantially improved (Figure 5). For each candidate we compute the probability

that the candidate will turn out to be a quasar. The

threshold can be chosen to be higher (producing a purer but less complete sample) or lower (producing a less reliable but more complete sample.) At the high-reliability end, by selecting

, we can construct a sample consisting of 89% quasars and only 11% non-quasars. Moreover, the majority of the non-quasars are BL Lac objects (which probably should be lumped in with the quasars), so the selective sample includes a total of 96.4% quasars and BL Lacs with only an amazingly small 3.6% contamination by other objects. This sample includes 60% of the quasars from the complete sample. On the other hand, we can still retain a fairly complete sample (

%) while increasing the sample reliability to 80% by rejecting only the least likely quasar candidates from the sample.

We plan to use this approach in an expanded quasar search using a much lower resolution radio survey. The poorer radio positions lead to many more false candidates, but the decision trees will allow us to maintain a reasonable quasar discovery rate nonetheless.

6. Summary

In this paper I have briefly reviewed methods for object classification. There are several methods available for classification; the oblique decision tree method is well-suited for the problems I have studied, but the other methods are also useful and can be better for other problems. The choice of object features and the construction of high quality training data sets are important steps in developing a classifier, as is measuring the accuracy of the classifier.

The use of oblique decision trees for two rather different applications was described. For Guide Star Catalog-II star/galaxy discrimination, the plate-to-plate variations presented a difficult problem that was solved by using the ranks of the parameters instead of the raw parameter values. For the FIRST Bright Quasar Survey, decision trees allow us to compute the probability that a candidate will be a quasar before taking a spectrum, thus making our ground-based observing programs more efficient. Certainly there are many other data analysis problems that could benefit from similar approaches.

Currently my work is focusing on improvements to the classification accuracy using more sophisticated voting and training methods (bagging, boosting, and variants.) There are many other interesting research topics in this area, such as the development of decision tree induction programs that incorporate knowledge of the noise in the parameters.

References

Freund, Y., & Schapire, R. E. 1996, in Proc. 13th International Conference on Machine Learning, (San Francisco: Morgan Kaufmann), 148

Heath, D., Kasif, S., & Salzberg, S. 1993, in Proc. of the 13th International Joint Conf. on Artificial Intelligence, (San Francisco: Morgan Kaufmann), 1002

Lasker, B. M., McLean, B. J., Jenkner, H., Lattanzi, M. G., & Spagna, A. 1995, in Future Possibilities for Astrometry in Space, eds. F. van Leeuven & M. Perryman, ESA SP-379

Murthy, S. K., Kasif, S., & Salzberg, S. 1994, J. Artificial Intelligence Res., 2, 1

White, R. L. 1997, in Statistical Challenges in Modern Astronomy II, eds. G. J. Babu & E. D. Feigelson (New York: Springer), 135