
|
NRAO's 300-Foot telescope was completed in 1962, having been designed to last ten years. After operating for 26 years, it collapsed in November 1988, due to a structural failure. The US Congress appropriated US$74.5M for a replacement antenna in June 1989. NRAO decided to build a 100-meter unblocked (off-axis) millimeter-wave active surface antenna, with laser rangefinders to control both mirror shape and pointing, and to call it the ``Green Bank Telescope'' [GBT]. The construction contract was signed with Radiation Systems, Inc., in December 1990, groundbreaking was May 1991 and the initial completion target was December 1994. There have been many delays due to various causes. Steel erection was finished in July 1999. At the time of writing this paper (November 1999), about half of the 2004 aluminum panels had been installed. Figure 1 shows the GBT as it looked in the Fall of 1999. Acceptance testing should occur during the first half of 2000.
The GBT
has a 100-meter circular clear aperture (i.e., no
secondary obscuration or support legs to scatter radiation) which is
centered 54 meters from the axis of a 208 meter diameter paraboloid
with 60 meter focal length; the actual dimensions of the primary
mirror are 100 X 110 meters. The collecting area is
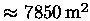 .
The mirror is composed of 2004 rectangular panels,
each about two meters on side, with 2209 actuators at their
corners. The surface accuracy goal for panel manufacturing was
.
The mirror is composed of 2004 rectangular panels,
each about two meters on side, with 2209 actuators at their
corners. The surface accuracy goal for panel manufacturing was
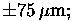 almost all of the panels meet this goal, and many are better.
The backup truss structure for the primary mirror has been designed to
produce a ``homologous'' paraboloid: in the absence of wind and
thermal gradient perturbations it will maintain its paraboloid shape
to about 1 mm RMS (10 ppm!) over the range
almost all of the panels meet this goal, and many are better.
The backup truss structure for the primary mirror has been designed to
produce a ``homologous'' paraboloid: in the absence of wind and
thermal gradient perturbations it will maintain its paraboloid shape
to about 1 mm RMS (10 ppm!) over the range
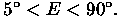
Except for its off-axis optics, the GBT is a conventional
wheel-and-track, fully steerable, radio antenna which can observe
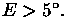 The azimuth track has a diameter of 64 m; at its
completion some years ago it was measured to be level to
The azimuth track has a diameter of 64 m; at its
completion some years ago it was measured to be level to
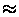 2 arcsec. The moving structure has a
mass of nearly 8000
metric tons, of which the tipping structure is about 5000 tons. The
elevation axle collimation error was
2 arcsec. The moving structure has a
mass of nearly 8000
metric tons, of which the tipping structure is about 5000 tons. The
elevation axle collimation error was 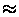 2 arcsec in the absence of thermal gradients when the two bearings were
set several years ago.
2 arcsec in the absence of thermal gradients when the two bearings were
set several years ago.
NRAO wants to operate the GBT at
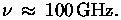 We must
maintain pointing to about 1/10 of
We must
maintain pointing to about 1/10 of
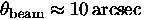 and surface shape to about
1/20 of
and surface shape to about
1/20 of
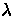
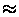 3 mm.
Distortions of the
structure and optics caused by wind pressure variations and thermal
gradients are likely to exceed these limits. Therefore, early
in the GBT project NRAO began to develop several types of sensors
(rangefinder, autocollimator, quadrant detector) to enable measurement
of the distortions so that they can be compensated. The laser
rangefinders are the key technology in the GBT project for achieving
closed-loop active optics control. The GBT control strategy is to
compensate all predictable wavefront errors with open-loop algorithms,
so that the closed-loop active optics servo will operate in a
nearly-null condition. One motivation for this strategy is the desire
that the telescope should degrade gracefully when the rangefinders
become unavailable for some reason.
3 mm.
Distortions of the
structure and optics caused by wind pressure variations and thermal
gradients are likely to exceed these limits. Therefore, early
in the GBT project NRAO began to develop several types of sensors
(rangefinder, autocollimator, quadrant detector) to enable measurement
of the distortions so that they can be compensated. The laser
rangefinders are the key technology in the GBT project for achieving
closed-loop active optics control. The GBT control strategy is to
compensate all predictable wavefront errors with open-loop algorithms,
so that the closed-loop active optics servo will operate in a
nearly-null condition. One motivation for this strategy is the desire
that the telescope should degrade gracefully when the rangefinders
become unavailable for some reason.
The GBT rangefinders (Figure 2)
use 780 nm semiconductor
lasers modulated at 1.5 GHz. Light returned by target retroreflectors
is detected and the signal is mixed with the transmitted signal to
detect the phase difference. The cycle length is
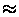 100 mm, so distances to targets must
be known within
100 mm, so distances to targets must
be known within
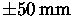 a priori. The prototype instruments had typical
typical range RMS
a priori. The prototype instruments had typical
typical range RMS
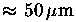 at 50 m with integration time
128 ms,2
but recently several of the production
instruments have demonstrated range RMS less than
at 50 m with integration time
128 ms,2
but recently several of the production
instruments have demonstrated range RMS less than
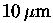 at ranges
greater than 150 m. The measurement rate capability is up to
5 ranges/s
for angular motions of order
at ranges
greater than 150 m. The measurement rate capability is up to
5 ranges/s
for angular motions of order
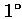 ,
,
 2 ranges/s
on random targets with motion of order a
radian. Slow drifts of the phase zero points are removed by measuring
internal reference prisms; one measurement per minute is sufficient to
maintain zero point error
2 ranges/s
on random targets with motion of order a
radian. Slow drifts of the phase zero points are removed by measuring
internal reference prisms; one measurement per minute is sufficient to
maintain zero point error
 The index of refraction of
air varies
The index of refraction of
air varies
 , and so air temperature
sensors and/or targets at known distances must be used to adjust the
index when reducing range measurements to true distance. At ranges of
order 100 m the beam diverges to several times the diameter of
a retroreflector prism, so the rangefinder angular positional
precision of 20 arcsec
is more than adequate. Approximate
coordinates of target retroreflectors on the GBT can be obtained from
surveying, telescope design geometry and the finite-element gravity
model (which will be improved with rangefinder data). The rangefinders
can range on each other, using prisms mounted on the back sides of
their scan mirrors. The rangefinder hardware has been described by
Payne, Parker and Bradley (1992, 1995); the
real-time
software
was
described at ADASS VIII (Creager 1999).
, and so air temperature
sensors and/or targets at known distances must be used to adjust the
index when reducing range measurements to true distance. At ranges of
order 100 m the beam diverges to several times the diameter of
a retroreflector prism, so the rangefinder angular positional
precision of 20 arcsec
is more than adequate. Approximate
coordinates of target retroreflectors on the GBT can be obtained from
surveying, telescope design geometry and the finite-element gravity
model (which will be improved with rangefinder data). The rangefinders
can range on each other, using prisms mounted on the back sides of
their scan mirrors. The rangefinder hardware has been described by
Payne, Parker and Bradley (1992, 1995); the
real-time
software
was
described at ADASS VIII (Creager 1999).
The corners of the 2004 primary mirror panels are supported by 2209
ball-screw actuators driven by DC motors with travel range
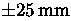 and LVDT position encoders. The
active surface control
system
contains five
VME-based real-time computers, which position their actuators to
within
and LVDT position encoders. The
active surface control
system
contains five
VME-based real-time computers, which position their actuators to
within
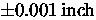
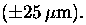 The number of
components in this system poses a major challenge for the GBT
project: 2209 actuators, kilometers of
wire, more than 20,000
connections. The homologous backup structure will depart from
paraboloidal shape by
The number of
components in this system poses a major challenge for the GBT
project: 2209 actuators, kilometers of
wire, more than 20,000
connections. The homologous backup structure will depart from
paraboloidal shape by
 1 mm RMS over
1 mm RMS over
 , so that gravity compensation
using the GBT
finite-element structural model will use only a few millimeters of
the full actuator travel range. The goal of the software servo will be to
move to the ``best-fitting paraboloid'' [BFP] at each elevation.
Actuator target positions will be computed as the zero point
determined from holography, plus the actuator structural model
displacements minus the BFP projected normal to surface, plus a
subreflector astigmatic aberration term, plus the closed-loop surface
correction function when available. About every 20 s the servo will
send new computed positions for the 2209 actuators to the active
surface control system.
, so that gravity compensation
using the GBT
finite-element structural model will use only a few millimeters of
the full actuator travel range. The goal of the software servo will be to
move to the ``best-fitting paraboloid'' [BFP] at each elevation.
Actuator target positions will be computed as the zero point
determined from holography, plus the actuator structural model
displacements minus the BFP projected normal to surface, plus a
subreflector astigmatic aberration term, plus the closed-loop surface
correction function when available. About every 20 s the servo will
send new computed positions for the 2209 actuators to the active
surface control system.
Each of the 2004 primary mirror panels will have a retroreflector
prism mounted in one corner, adjacent to an actuator. Six
rangefinders on the feedarm will trilaterate to these prisms
(Figure 33).
Measuring all of the prisms will take many minutes and so,
in practice, we expect that the surface servo algorithm will measure
only 94 of the prisms (
 15 m
spacing), taking less than
one minute. Wind variations will move the feedarm during the
measurements, and so repeated observations of a small set of reference
retroreflectors must be interleaved to enable adjustment to a
consistent coordinate system. Structural vibrations at modal
frequencies due to wind turbulence will be corrected by using the
structural model eigenvectors scaled by amplitude and phase values
determined from accelerometer and quadrant detector data. Corrected
ranges will be used to solve for a time-varying Zernike polynomial
expansion of the wavefront error. The coefficients of the Zernike
expansion will be passed to the open-loop surface servo. This will
create a closed-loop surface servo operating in a
measure-compute-actuate cycle with period less than a minute,
synchronized with the
15 m
spacing), taking less than
one minute. Wind variations will move the feedarm during the
measurements, and so repeated observations of a small set of reference
retroreflectors must be interleaved to enable adjustment to a
consistent coordinate system. Structural vibrations at modal
frequencies due to wind turbulence will be corrected by using the
structural model eigenvectors scaled by amplitude and phase values
determined from accelerometer and quadrant detector data. Corrected
ranges will be used to solve for a time-varying Zernike polynomial
expansion of the wavefront error. The coefficients of the Zernike
expansion will be passed to the open-loop surface servo. This will
create a closed-loop surface servo operating in a
measure-compute-actuate cycle with period less than a minute,
synchronized with the
 20 s
period of the open-loop
surface servo. The goal is to track and correct large-scale,
slowly-changing thermal- and wind-induced distortions of the backup
structure. Note that ranges across the 100 m
steel backup
structure will be quite sensitive to thermal expansion:
20 s
period of the open-loop
surface servo. The goal is to track and correct large-scale,
slowly-changing thermal- and wind-induced distortions of the backup
structure. Note that ranges across the 100 m
steel backup
structure will be quite sensitive to thermal expansion:
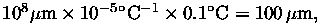 so
so
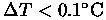 will be easily detectable in a single rangefinder
measurement.
will be easily detectable in a single rangefinder
measurement.
The relative heights of the corners of the panels supported by each
actuator will be adjusted to better than
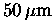 using a special
tool developed by NRAO, and the retroreflector prism heights relative
to the panels are predictable to
using a special
tool developed by NRAO, and the retroreflector prism heights relative
to the panels are predictable to
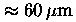 RMS.
Therefore, in
principle, trilateration by the rangefinders can determine proper zero
points for the actuators with high precision, and holographic
calibration may turn out to be used only as a sanity check.
RMS.
Therefore, in
principle, trilateration by the rangefinders can determine proper zero
points for the actuators with high precision, and holographic
calibration may turn out to be used only as a sanity check.
The Gregorian subreflector is an
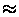 8 m
diameter portion
of an ellipsoid with
8 m
diameter portion
of an ellipsoid with
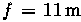 , with
, with
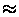 50
panels set to
50
panels set to
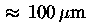 RMS by photogrammetry. The subreflector will be
adjusted so that its two foci will coincide with the primary mirror
prime focal point [PFP] and the feedhorn phase center when
RMS by photogrammetry. The subreflector will be
adjusted so that its two foci will coincide with the primary mirror
prime focal point [PFP] and the feedhorn phase center when
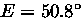 . Gravity deflection moves the
feedarm relative to the PFP
. Gravity deflection moves the
feedarm relative to the PFP
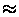 23 cm;
the focus tracking algorithm compensates
this by moving the subreflector. Ray tracing analysis shows that the
optimum focus tracking algorithm can compensate the
23 cm;
the focus tracking algorithm compensates
this by moving the subreflector. Ray tracing analysis shows that the
optimum focus tracking algorithm can compensate the
 -order
aberrations curvature (focus), coma and spherical aberration
exactly, leaving only 0.4 mm
of residual astigmatism at the extremes of elevation:
-order
aberrations curvature (focus), coma and spherical aberration
exactly, leaving only 0.4 mm
of residual astigmatism at the extremes of elevation:
| Wavefront Errors | |||||||
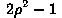 |
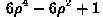 |
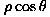 |
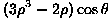 |
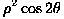 |
|||
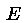 |
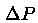 |
Curv | SphAb | Tilt | Coma | Astm | 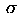 |
| d | mm | mm | mm | 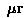 |
mm | mm | 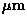 |
| 0 | -19.6 | -0.0 | 0.0 | -2 | -0.0 | -0.4 | 12 |
| 20 | -16.0 | -0.0 | 0.0 | -1 | -0.0 | -0.2 | 7 |
| 44 | -0.0 | -0.0 | 0.0 | -0 | -0.0 | -0.0 | 0 |
| 70 | 28.8 | 0.0 | -0.0 | -0 | 0.0 | 0.3 | 7 |
| 90 | 56.0 | 0.0 | -0.0 | -1 | 0.1 | 0.4 | 12 |
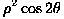 term to the open-loop surface servo. In the above table
term to the open-loop surface servo. In the above table
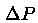 is the change of total pathlength through the GBT and
is the change of total pathlength through the GBT and
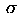 is the residual (
is the residual (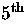 -order) wavefront error.
-order) wavefront error.
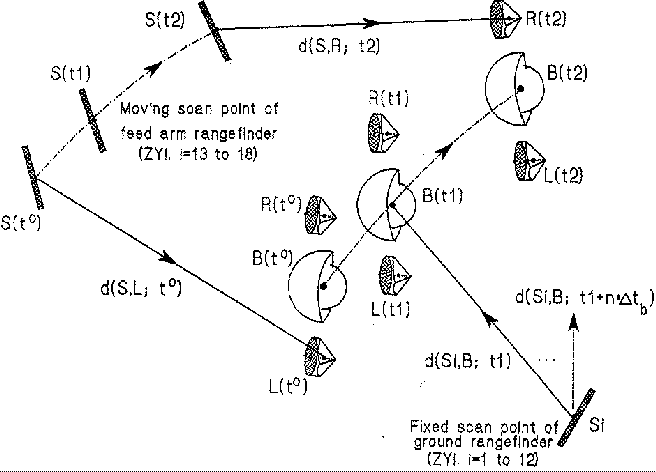
There are six retroreflector prisms attached to the subreflector panels; their positions relative to the ellipsoid foci were determined by analysis of photogrammetric data. The feedarm rangefinders will observe these prisms to locate the subreflector in the primary mirror closed-loop servo coordinate system. Slow changes in the feedarm position relative to the open-loop gravity model prediction will be determined as a part of the closed-loop surface servo, and these will be added to the open-loop focus-tracking algorithm, thereby making it closed-loop too.
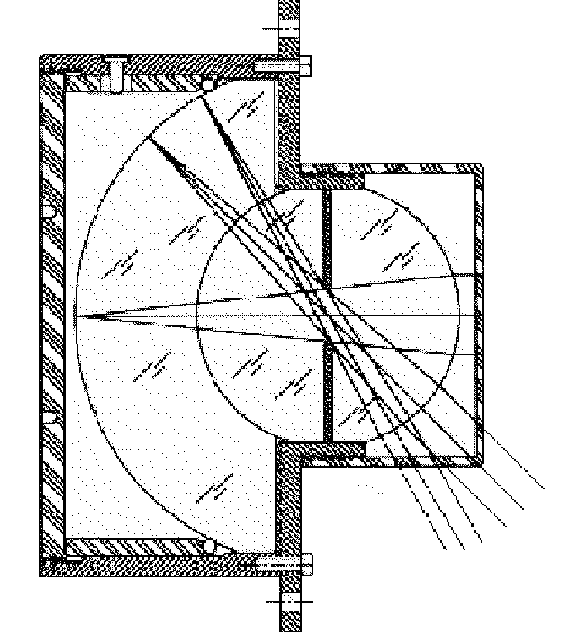
The GBT will use a ``traditional'' pointing model with about 10 terms. The rangefinders will be used to calibrate many, and perhaps all, of the pointing coefficients because the metrological determination is expected to be more accurate than the traditional technique of fitting to radio source observations, but this model will still be used as an open-loop pointing servo.
Wind forces and thermal gradients will cause the beam to deviate from
the position indicated by encoders after the traditional model
corrections have been applied. The GBT has 12 of its rangefinders
mounted on stable ground monuments at
120 m
radius from the
pintle bearing (Figure 4).
These will be used to range on
retroreflectors attached to the alidade and tipping structure so that
these unpredictable changes of orientation can be measured. This
process has been simulated by generating fake data for 12 ground
rangefinders measuring 6 retroreflectors at
2 ranges/s
during 3 s
to produce 72 ranges with
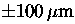 noise
added. The simulation assumed the tipping structure is moving with
constant velocity in Az and El. The Gaussfit least-squares program
(Jefferys et al. 1988) was used to fit the data, using the model shown
in Figure 5. The simulated
orientation was
noise
added. The simulation assumed the tipping structure is moving with
constant velocity in Az and El. The Gaussfit least-squares program
(Jefferys et al. 1988) was used to fit the data, using the model shown
in Figure 5. The simulated
orientation was
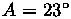 ,
,
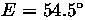 ,
and angular velocities were 1 mr/s (200 arcsec/s,
,
and angular velocities were 1 mr/s (200 arcsec/s,
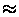 10X sideral) in both axes. The
simulated GBT tipping structure differed from nominal geometry due to
an assumed
10X sideral) in both axes. The
simulated GBT tipping structure differed from nominal geometry due to
an assumed
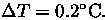 The simulated solutions have
The simulated solutions have
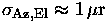 (0.2 arcsec),
(0.2 arcsec),
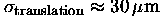 ,
and
,
and
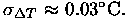 It is interesting to note that Gaussfit,
even spawned by a Perl script and with various other inefficiencies,
proved to be faster than real-time on the author's
450 MHz P-II. Therefore, it is possible that this simulation program
will be adapted for production use! In practice the model-fitting
technique will be slightly different from the one used in this
simulation: we will solve for the difference between the observed
orientation and the commanded trajectory. This is because this offset
is independent of the trajectory shape.
It is interesting to note that Gaussfit,
even spawned by a Perl script and with various other inefficiencies,
proved to be faster than real-time on the author's
450 MHz P-II. Therefore, it is possible that this simulation program
will be adapted for production use! In practice the model-fitting
technique will be slightly different from the one used in this
simulation: we will solve for the difference between the observed
orientation and the commanded trajectory. This is because this offset
is independent of the trajectory shape.
There are retroreflectors attached to the elevation bearing housings. Ranges to them from the ground rangefinders (see Figure 4) will be analyzed to infer changes in the elevation axis collimation angle and the azimuth zero point. It is likely that these corrections will be applied directly to the corresponding coefficients of the traditional pointing model. If so, the model fitting technique discussed above will be determining pointing corrections due to distortions of the tipping structure, independent of the distortions of the alidade structure determined by measuring the elevation bearings. Anecdotal evidence for other large radio antennas suggests that typically about half of the total pointing error occurs in the alidade structures.
/* Gaussfit model which fits translation, orientation & temperature
parameters to observations of range to retroreflector prisms
which are attached to a moving truss structure, assuming that the
truss is rigid and that the angular velocities and the rangefinder
and prism coordinates are known. */
constant pr[ranger,axisr]; /* XYZ_ground of rangefinder */
constant pc[cube,axisc]; /* XYZ_truss of retroreflector */
constant coefficient; /* per degC (1.2e-5 for steel) */
constant eulervelocity[axisp]; /* known angular velocities */
parameter translate[axisp]; /* Delta_XYZ of truss */
parameter euler[axisp]; /* Az=euler[0],El=euler[1],t=0 */
parameter temperature; /* Delta_T of truss [degC] */
data time, r, c;
observation range; /* rangefinder 'r' to prism 'c' at 'time' */
main() {
variable i, cp[3], sum, computed, naxes=3;
while (import()) {
for (i = 0; i < naxes; i = i + 1)
cp[i] = pc[c,i] * expansion(temperature,coefficient);
about_z(cp, (euler[2]+eulervelocity[2]*time));
about_x(cp, (euler[1]+eulervelocity[1]*time));
about_z(cp, (euler[0]+eulervelocity[0]*time));
sum = 0.0; for (i = 0; i < naxes; i = i + 1) {
cp[i] = cp[i] + translate[i];
sum = sum + (cp[i] - pr[r,i])^2;
}
computed = sqrt(sum);
export(range - computed);
}
}
about_z(v, a) { variable temp;
temp = +v[0]*cos(a) +v[1]*sin(a);
v[1] = -v[0]*sin(a) +v[1]*cos(a);
v[0] = temp;
}
about_x(v, a) { variable temp;
temp = +v[1]*cos(a) +v[2]*sin(a);
v[2] = -v[1]*sin(a) +v[2]*cos(a);
v[1] = temp;
}
expansion(temp, tempcoeff) {
return (1 + temp * tempcoeff);
}
|
 |
 |
NRAO hopes that eventually this ground-referenced pointing technique
will be able to point the beam absolutely (of course, until we are
confident about absolute pointing we intend to use radio sources for
local zero point pointing corrections in the usual fashion). A key
requirement for absolute pointing of the wavefront produced by the
primary mirror is to be able to determine the locations of the feedarm
rangefinders relative to the ground. The enormous primary mirror
blocks many of the lines-of-sight needed for such determination. We
wish that we could ``bend'' the lines-of-sight around the obstruction;
this idea led to a concept which we call ``triplet'' retroreflectors:
one retro faces in one direction and two other retros face in the
opposite direction, with the reflection point of the first retro
coincident with the bisector of the line connecting the other two
retros. Conventional corner-cube prisms operate to
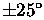 off-axis, covering only
off-axis, covering only
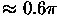 steradian
steradian
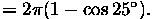 The desire for
increased solid angle coverage caused NRAO to contract with the
Optical Sciences Center in Tucson to produce a set of spherical
retroreflectors (Goldman 1996) which can be deployed to critical
points on the structure where wider-angle capability is needed; the
The desire for
increased solid angle coverage caused NRAO to contract with the
Optical Sciences Center in Tucson to produce a set of spherical
retroreflectors (Goldman 1996) which can be deployed to critical
points on the structure where wider-angle capability is needed; the
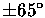 off-axis capability (see
Figure 6) of the
retrospheres covers
off-axis capability (see
Figure 6) of the
retrospheres covers
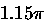 steradian
.4
Six triplet retros will be installed
around the rim of the primary mirror. Measurements of these triplets
from the ground will yield pointing corrections and measurements from
the feedarm by the surface servo (note the laser beams intersecting at
the rim of the primary in Figure 4, and compare the schematic
in Figure 6) will refer the surface prism measurements to the
triplet prism pairs (using the geometric mean of the ranges), thereby
determining the wavefront orientation referred to the ground
monuments. The schematic in Figure 6 reminds us that we will be
ranging on the moving triplets from a moving feedarm as well as from
the ground, without the simplification of simultaneity.
steradian
.4
Six triplet retros will be installed
around the rim of the primary mirror. Measurements of these triplets
from the ground will yield pointing corrections and measurements from
the feedarm by the surface servo (note the laser beams intersecting at
the rim of the primary in Figure 4, and compare the schematic
in Figure 6) will refer the surface prism measurements to the
triplet prism pairs (using the geometric mean of the ranges), thereby
determining the wavefront orientation referred to the ground
monuments. The schematic in Figure 6 reminds us that we will be
ranging on the moving triplets from a moving feedarm as well as from
the ground, without the simplification of simultaneity.
Creager, R. E. 1999, in ASP Conf. Ser., Vol. 172, Astronomical Data Analysis Software and Systems VIII, ed. D. M. Mehringer, R. L. Plante, & D. A. Roberts (San Francisco: ASP), 91
Goldman, M. A. 1996, ``Ball retroreflector optics'', NRAO GBT Memo 148
Jefferys, W. H., Fitzpatrick, M. J., McArthur, B. E., & McCartney, J. E. 1988, ``User's Manual--GaussFit: A system for least squares and robust estimation'', follow FTP link in HST Astrometry Team software Web page
Payne, J. M., Parker, D. H., & Bradley, R. F. 1992, Rev.Sci.Instr., 3311
Payne, J. M., Parker, D. H., & Bradley, R. F. 1995, ``Optical electronic distance measuring apparatus with movable mirror'', US Patent 5,455,670 filed May 27, 1993, and issued October 3, 1995
Wells, D. 1995, in ASP Conf. Ser., Vol. 77, Astronomical Data Analysis Software and Systems IV, ed. R. A. Shaw, H. E. Payne, & J. J. E. Hayes (San Francisco: ASP), 148
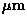 is approximately the thickness of a typical sheet of paper!
is approximately the thickness of a typical sheet of paper!
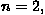 , it would act as a
retroreflector covering up to
, it would act as a
retroreflector covering up to
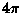 steradian.
In the past this
was only a theoretical possibility, because such material was not
available. Recently the GBT metrology group learned of the development
of retrospheres made of a lanthanide material which does have
steradian.
In the past this
was only a theoretical possibility, because such material was not
available. Recently the GBT metrology group learned of the development
of retrospheres made of a lanthanide material which does have
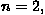 ;
the group expects to test these devices when they become available. If
they prove satisfactory, the bulky and expensive ``triplet''
assemblies covering
;
the group expects to test these devices when they become available. If
they prove satisfactory, the bulky and expensive ``triplet''
assemblies covering
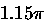 could be replaced by compact single
spheres covering almost
could be replaced by compact single
spheres covering almost
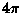 .
.