Next: The Status of the Second Generation Digitized Sky Survey and Guide Star Catalog
Up: Archiving
Previous: Using DVD-R for Storing Astronomical Archive Data (cont'd)
Table of Contents -
Subject Index -
Author Index -
PS reprint -
Kunszt, P. Z., Szalay, A. S., Csabai, I., & Thakar, A. R. 2000, in ASP Conf. Ser., Vol. 216, Astronomical Data
Analysis Software and Systems IX, eds. N. Manset, C. Veillet, D. Crabtree (San Francisco: ASP), 141
The Indexing of the SDSS Science Archive
P. Z. Kunszt, A. S. Szalay, I. Csabai1, A. R. Thakar
Dept. of Physics and Astronomy,
Johns Hopkins University,
Baltimore, MD 21218
Abstract:
The Spatial Indexing used in the
Sloan Digital
Sky Survey (SDSS) Science Archive
divides
the spherical surface into triangles in a hierarchical scheme
resulting in roughly equal surface areas at each level, which is a big
advantage over other schemes. The location of a point on the sky may
be given by the unique index id to any level, refining it with each
step. This naming scheme is being used successfully in other catalogs,
too, like GSC-II and GAIA. The use of the Spatial Index in the SDSS
is two-fold, a level-5 index is used to partition the bulk data, and a
high-resolution level-14 index id is assigned to each data point to
enable quick lookup and proximity searches.
Use of this indexing scheme in more catalogs will enormously simplify
cross-matching of objects. Using a new computing paradigm, we recently
realized a quantum leap in performance that makes this scheme
competitive with bit-interleaving and requires very little memory.
The Flux-space Indexing used is a traditional 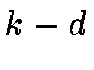 tree. The space is 5
dimensional, 5 being the number of SDSS-filters. The specialization to
astronomical data has been achieved by modeling the location of the
main branch in this space and applying the
tree. The space is 5
dimensional, 5 being the number of SDSS-filters. The specialization to
astronomical data has been achieved by modeling the location of the
main branch in this space and applying the 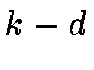 tree subdivisions only
to its confined area. The outliers are indexed separately. Most of
the interesting data points come directly from the outlier part of the
index, with no additional analytical effort.
tree subdivisions only
to its confined area. The outliers are indexed separately. Most of
the interesting data points come directly from the outlier part of the
index, with no additional analytical effort.
Additionally, the key-lookup index feature of object-oriented
databases is exploited for much-used parameters like flags.
Indexing is one of the major issues which has to be addressed by
modern astronomical database systems that deal with multiple terabytes
of data. Most scientific queries are concerned only with a fraction of
the whole data volume, the query being confined to a finite volume in 3D
space and in color space. Good indexing techniques reduce the data
volume that is effectively scanned on by several orders of magnitudes
for such confined queries (ideally, only the queried data is physically
read from disk).
The SDSS Science Archive (SX) makes use of two indexing techniques for
user queries. (The SDSS project and Science Archive is described in
further detail in articles by A. S. Szalay and by A. R. Thakar in this
volume.) The first index is called the Hierarchical Triangular Mesh
(HTM), which is used to subdivide the surface of the unit sphere into
roughly equal-sized spherical triangles. (This method was advocated
by P. Barrett (1994); proposed in detail by A. Szalay, R. Brunner
et al., 1996. See also H. Samet, 1990) The HTM, a quad-tree, is used
as the spatial index of the SX.
The second major index is an enhanced k-d tree that is used on the
5-dimensional color space of the SDSS data (the dedicated SDSS camera
has 5 passband filters). Both indices are used to reduce the total
data volume that needs to be scanned for the user query to complete.
Object coordinates are located on the surface of the celestial (unit)
sphere, usually given by 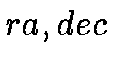 . For the HTM, we will convert to
Cartesian coordinates to simplify our notation. The HTM is a
quad-tree, its top nodes are the 8 segments that define the octahedron
on the sphere (its sides are given by the intersection of the sphere
with the
. For the HTM, we will convert to
Cartesian coordinates to simplify our notation. The HTM is a
quad-tree, its top nodes are the 8 segments that define the octahedron
on the sphere (its sides are given by the intersection of the sphere
with the 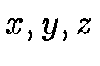 planes). The 6 corners of the octahedron are,
enumerated from 0 to 5 as follows:
planes). The 6 corners of the octahedron are,
enumerated from 0 to 5 as follows: 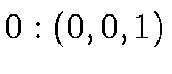 ;
; 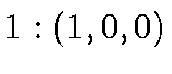 ;
; 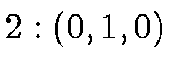 ;
; 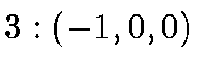 ;
; 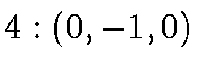 ;
; 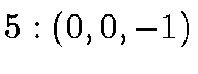 .
.
The nodes of the HTM quad-tree are always spherical triangles with great
circle segments connecting the corners. The triangles are specified
by their vertices, the vertices always given in counterclockwise
order. The 8 root nodes are, using the enumeration of the 6 octahedron
corners from above: 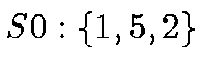 ;
; 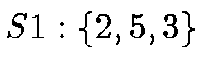 ;
; 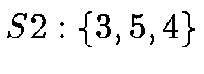 ;
; 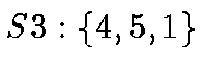 ;
; 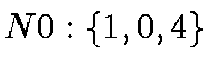 ;
; 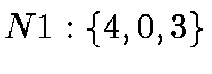 ;
; 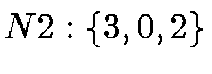 ;
; 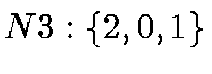 .
.
Figure 1:
Subdividing a triangle recursively into 4 new ones. Here we show
planar triangles for simplicity. The vertex order is changed on the
new triangles,  labeling the old triangle's corners. The naming
scheme is to append the parent vertex's index to the parent's name.
labeling the old triangle's corners. The naming
scheme is to append the parent vertex's index to the parent's name.
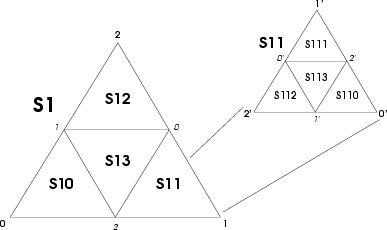 |
The quad-tree is obtained by subdividing the triangles into 4 new
triangles, using the current corners and the side-midpoints as the
corners for the new triangles (as illustrated by figure
1).
The new nodes obtained in this fashion are named by appending the
index 0,1,2,3 to the parent's name, depending which vertex the new
triangle shares with its parent (3 for the middle triangle).
At each level 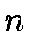 of the HTM, the average triangle area is
of the HTM, the average triangle area is 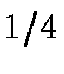 of
their parent triangle's average area, i.e. exactly
of
their parent triangle's average area, i.e. exactly
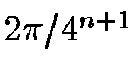 . There will be no triangle, however, with exactly this
area at any but the root level. Already at the first subdivision, the
middle triangles have different areas and side-lengths (the angle at
each corner of the root triangles is exactly
. There will be no triangle, however, with exactly this
area at any but the root level. Already at the first subdivision, the
middle triangles have different areas and side-lengths (the angle at
each corner of the root triangles is exactly 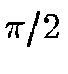 , which is not
true anymore for the next level). The scatter of the different
triangle areas remains within
, which is not
true anymore for the next level). The scatter of the different
triangle areas remains within 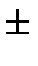 70% of the mean area at any
level. It can be shown that the ratio of the minimal and maximal
triangle areas quickly converges to a constant value (roughly 2).
70% of the mean area at any
level. It can be shown that the ratio of the minimal and maximal
triangle areas quickly converges to a constant value (roughly 2).
The length of each triangle side is thus also distributed between a
minimal and maximal length for each level. It is easy to see that the
minimal side length is given by the subdivisions of the 3 major big
circles that define the 8 root nodes, giving minimal side lengths of
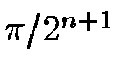 at level
at level 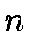 . It can be shown that the maximal
side-length converges to
. It can be shown that the maximal
side-length converges to 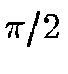 times the minimal length. So for
example at level 14, the side-lengths are between 20 and 30 arcseconds.
times the minimal length. So for
example at level 14, the side-lengths are between 20 and 30 arcseconds.
The HTM name can be bit-encoded into a single integer (2 bits per
level), giving an HTM ID for each object. The ID up to level 14 can be
stored in a 32-bit integer, and up to level 30 in a 64-bit integer.
We suggest that each database stores the HTM ID for each object to a
level depth where the triangle side-length reaches the object's
size. For a catalog with angular resolution of 20 arcseconds it does
not make sense to go beyond level 14.
To cross-match two catalogs, we retrieve each object's location
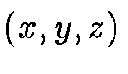 from the catalog with the better resolution (i.e. where the
ID is stored to a higher level
from the catalog with the better resolution (i.e. where the
ID is stored to a higher level 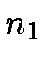 ) and determine the triangles that
are in its vicinity at the HTM level of the second catalog
(
) and determine the triangles that
are in its vicinity at the HTM level of the second catalog
(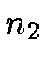 ). This is done by finding all the triangles in level
). This is done by finding all the triangles in level 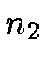 that
are touched by a sphere segment with origin at
that
are touched by a sphere segment with origin at 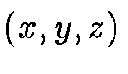 and diameter
of the minimal side-length of level
and diameter
of the minimal side-length of level 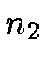 ; at most 6
triangles. Now we just look up these 6 IDs in the second catalog
whether they match any of the objects within.
; at most 6
triangles. Now we just look up these 6 IDs in the second catalog
whether they match any of the objects within.
This procedure is basically an ID lookup in both catalogs. If the ID is
key indexed in both catalogs, the cross-matching should be working with
the same speed as the lookup of the catalog objects one by one,
i.e. we have an order(N) algorithm.
The 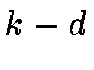 tree used in the SX differs from standard
tree used in the SX differs from standard 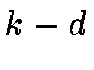 trees in two
respects. The first is that we don't use the standard method to cut
the data volume in alternating dimensions but we calculate the
bounding box of each cell at each level and cut in the direction with
the largest box side. Thus we get a minimal aspect ratio
trees in two
respects. The first is that we don't use the standard method to cut
the data volume in alternating dimensions but we calculate the
bounding box of each cell at each level and cut in the direction with
the largest box side. Thus we get a minimal aspect ratio 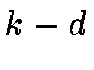 tree.
It has been shown recently (Duncan 1999) that
tree.
It has been shown recently (Duncan 1999) that 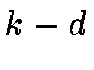 trees
constructed in this way perform very well as generic indexing trees
for various aspects of indexed lookup.
trees
constructed in this way perform very well as generic indexing trees
for various aspects of indexed lookup.
The second enhancement is to model the object's predicted location in
color-space (the stellar locus for example) and construct a convex
hull of that area. The first ``cut'' of our 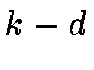 -tree is deciding
whether an object lies inside or outside the predicted area. If it is
an outlier, it is stored in one branch, and the rest is indexed using
the
-tree is deciding
whether an object lies inside or outside the predicted area. If it is
an outlier, it is stored in one branch, and the rest is indexed using
the 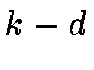 -tree described above. In such a way, many of the most
interesting objects are found using a simple index query.
-tree described above. In such a way, many of the most
interesting objects are found using a simple index query.
The physical data layout of the SX makes use of both the HTM and the
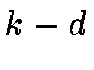 -tree. The underlying commercial database of SX is Objectivity,
which is an object-oriented DBMS. In an Objectivity federation,
``databases'' are single files that contain the objects, grouped into
``containers''. In the SX, we define the databases to be the level-5
leaf nodes of the HTM, (defining the database file name) and we order
the objects inside the database according to their
-tree. The underlying commercial database of SX is Objectivity,
which is an object-oriented DBMS. In an Objectivity federation,
``databases'' are single files that contain the objects, grouped into
``containers''. In the SX, we define the databases to be the level-5
leaf nodes of the HTM, (defining the database file name) and we order
the objects inside the database according to their 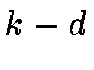 -tree leaf
node number. This way, if we query for objects confined to a limited
area on the 3D sphere, we only need to open the level-5 HTM databases
that contain the corresponding area. If a query involves a domain of
color space (5-dimensional for SDSS), we do need to open all
databases, but the data will be localized close to each other in each
of them. This makes very effective use of the hardware and software
caching mechanisms.
-tree leaf
node number. This way, if we query for objects confined to a limited
area on the 3D sphere, we only need to open the level-5 HTM databases
that contain the corresponding area. If a query involves a domain of
color space (5-dimensional for SDSS), we do need to open all
databases, but the data will be localized close to each other in each
of them. This makes very effective use of the hardware and software
caching mechanisms.
The current implementation of the HTM is available on the
SDSS Science Archive Website
in C, C++ and JAVA. The code has been tested on various Unix platforms
(Solaris, OSF/1, IRIX, Linux) and on Windows NT/98/95. It should run
on other platforms as well. We do want to encourage everyone building
catalogs to include the HTM ID with their catalog objects so that
cross-matching between catalogs is simplified. The software also comes
with a variety of query capabilities; basically any shape on the
spherical surface can be submitted to it to get the triangles that are
fully contained or partially contained within that surface. The code
is freely available.
References
Barrett, P. 1994, in ASP Conf. Ser., Vol. 77, Astronomical Data Analysis
Software and Systems IV, ed. R. A. Shaw, H. E. Payne, & J. J. E. Hayes
(San Francisco: ASP), 492
Duncan, C. 1999, Thesis, Johns Hopkins Univ., Dept. of Computer
Science
Samet, H. 1990, Applications of Spatial Data Structures and
The Design and Analysis of Spatial Data Structures; Addison-Wesley.
Szalay, A. S. 2000, this volume, 405
Szalay, A. S., Brunner, R., et. al. proposal, 1996
Thakar, A. 2000, this volume, 231
Footnotes
- ... I. Csabai1
- Department of Physics, Eötvös Lóránt University Budapest, Hungary
© Copyright 2000 Astronomical Society of the Pacific, 390 Ashton Avenue, San Francisco, California 94112, USA
Next: The Status of the Second Generation Digitized Sky Survey and Guide Star Catalog
Up: Archiving
Previous: Using DVD-R for Storing Astronomical Archive Data (cont'd)
Table of Contents -
Subject Index -
Author Index -
PS reprint -
adass@cfht.hawaii.edu
![]() tree. The space is 5
dimensional, 5 being the number of SDSS-filters. The specialization to
astronomical data has been achieved by modeling the location of the
main branch in this space and applying the
tree. The space is 5
dimensional, 5 being the number of SDSS-filters. The specialization to
astronomical data has been achieved by modeling the location of the
main branch in this space and applying the ![]() tree subdivisions only
to its confined area. The outliers are indexed separately. Most of
the interesting data points come directly from the outlier part of the
index, with no additional analytical effort.
tree subdivisions only
to its confined area. The outliers are indexed separately. Most of
the interesting data points come directly from the outlier part of the
index, with no additional analytical effort.
