Next: Cosmic Ray Rejection with NGST
Up: Data Compression
Previous: Contour-Based Image Compression for Fast Real-Time Coding
Table of Contents -
Subject Index -
Author Index -
Search -
PS reprint -
PDF reprint
Nieto-Santisteban, M. A., Fixsen, D. J., Offenberg, J. D., Hanisch, R. J., & Stockman, H. S. 1999, in ASP Conf. Ser., Vol. 172, Astronomical Data Analysis Software and Systems VIII, eds. D. M. Mehringer, R. L. Plante, & D. A. Roberts (San Francisco: ASP), 137
Data Compression for NGST
María A. Nieto-Santisteban, Dale J. Fixsen1, Joel D. Offenberg2, Robert J. Hanisch, H. S. (Peter) Stockman
Space Telescope Science Institute, 3700 San Martin Drive, MD 21218
Email: nieto, fixsen, offenbrg, hanisch, stockman@stsci.edu
URL: http://ngst.gsfc.nasa.gov/cgi-bin/iptsprodpage?Id=14
Abstract:
The immense amount of data that the Next Generation Space Telescope
(NGST) will produce and its distant orbit from Earth make it mandatory
to do some amount of on-board image processing and data compression.
This paper gives a summary of the performance of several lossless
compression methods. We also show results of prescaling the image
prior to compression using a square-root function. This imposes a
slightly lossy compression, but the scaling can be adjusted so as to
retain the desired number of noise bits.
The Next Generation Space Telescope (NGST) will produce about 600
GB/day, assuming we use the NASA Yardstick 8k x 8k NIR camera
(16 bits/pixel), save and transmit 64 non-destructive read-outs per
image, and the camera is in continuous use (about 80 observations/day,
103 s each). However, with an L2 halo orbit, the NASA NGST study
estimates a downlink rate of 5.35 GB/day using X-band. Clearly the
volume of data to downlink must be reduced by at least a factor of
100.
Astronomical images are noisy. This fact makes them difficult to
compress by lossless compression algorithms such as Huffman,
Lempel-Ziv, run-length, or arithmetic code. However, they also have
the virtue of showing similar values among adjacent pixels. Techniques
such as Rice's algorithm (Rice, Yeh, & Miller 1993) and derivatives
(White & Becker 1998; Stiavelli & White 1997) can take advantage of
this. In this paper, we present how some of these compression
techniques would work with NGST images. Unfortunately, these lossless
algorithms give us compression ratios that still exceed the telemetry
guidelines. We have also looked into the feasibility of doing lossy
compression by scaling the original image prior to the lossless
compression. Under this scheme, we find substantial data reduction
with a negligible effect on the data quality.
The first and more important compression ratio, 64:1, is
obtained after applying a cosmic ray rejection process and fitting 64
readouts into one single image (Offenberg et al. 1999). (In fact, 65
readouts involve the cosmic ray rejection and fitting
process, however, the first readout [dark frame] should be rarely
downlinked.)
An additional compression factor close to 3:1 is achieved by
using predictive compression techniques such as the Lossless JPEG and
Rice's algorithm. Dictionary-based lossless compression programs such
as ``gzip'' and ``compress'' present lower compression ratios (see
Table 1).
We can further reduce the data volume by using a prescaled image as
input to the lossless encoder. The prescaling process, based on the
square-root function, can be adjusted so as to retain as many bits of
noise as desired. Similar results are obtained independently of the
lossless compression technique in use, with overall compression ratios
of 4:1 (keeping 4 noise bits), up to as much as 8:1
(keeping 1 noise bit).
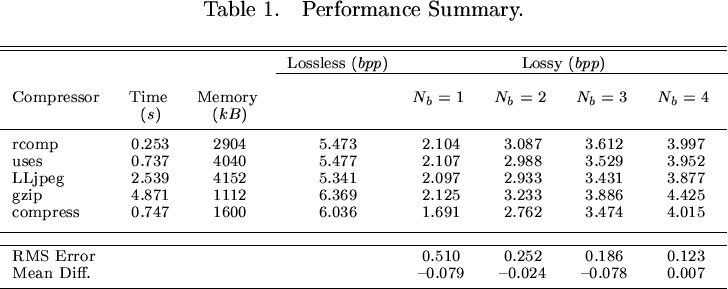
This table give the summary in time, memory and
compression rates (lossless and lossy) achieved for five lossless
compressors. As test input data, a simulated NGST deep image was
used (1024 x 1024, 2 bytes per pixel, DN units) obtained in a
103s exposure after the cosmic ray removal and slope fitting
algorithm. A readout noise of 15 electrons and a gain of 4 are
assumed. Scaling function applied for lossy compression,
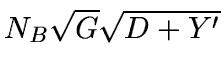 . Values of the Normalized Root-Mean-Square
Error and Mean Difference are also shown. Rcomp and uses
are implementations of the Rice algorithm. Rcomp was developed
at STScI by Rick White. Uses was developed at University of New
Mexico Microelectronics Research Center. LLjpeg is a lossless
JPEG developed by the PVRG-JPEG. gzip and compress are the
well known general purpose compression programs based on dictionary
techniques. The tests were run on a Sun Ultra 10.
. Values of the Normalized Root-Mean-Square
Error and Mean Difference are also shown. Rcomp and uses
are implementations of the Rice algorithm. Rcomp was developed
at STScI by Rick White. Uses was developed at University of New
Mexico Microelectronics Research Center. LLjpeg is a lossless
JPEG developed by the PVRG-JPEG. gzip and compress are the
well known general purpose compression programs based on dictionary
techniques. The tests were run on a Sun Ultra 10.
Pure noise by its very nature is impossible to compress. In order to
compress the data and retain as much information as possible, it is
useful to eliminate the low order data bits (i.e., the
noise). Truncating the bits at some level is one possibility, but the
noise level differs across the picture. We describe a simple
approximation to the noise which is carried in the data itself.
There are two important sources of non-systematic noise: the Poisson
distribution of the photons themselves and the readout noise in the
readout electronics. From these two sources, a reasonable
approximation to the standard deviation is
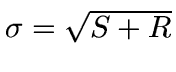 where
S is the signal in units of photons (or equivalently electrons) and
R is the readout variance in the same units.
where
S is the signal in units of photons (or equivalently electrons) and
R is the readout variance in the same units.
In order to simplify both the encoding and the decoding we make an
approximation to
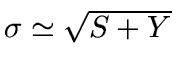 where S is the readout
(in electrons) and Y is a number which we will derive from the
readout variance R. First note an absolute offset does not incur a
significant penalty in data transmission since virtually any lossless
data compression scheme will use very little bandwidth to transmit the
offset in a large block of data. The key then is to get a good
approximation to the derivative. Note if we use
where S is the readout
(in electrons) and Y is a number which we will derive from the
readout variance R. First note an absolute offset does not incur a
significant penalty in data transmission since virtually any lossless
data compression scheme will use very little bandwidth to transmit the
offset in a large block of data. The key then is to get a good
approximation to the derivative. Note if we use 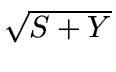 for
for
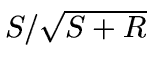 for large S the derivatives already match. By taking
the derivatives with respect to S and setting them equal to each
other at S = 0 we have Y = R/4. Thus we can use
for large S the derivatives already match. By taking
the derivatives with respect to S and setting them equal to each
other at S = 0 we have Y = R/4. Thus we can use 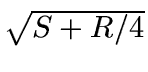 and
truncation as a lossy compression to reduce the data dynamic range in
an approximately uniform way. Since our NGST simulation is in data
numbers (DN), we must rescale this formula to
and
truncation as a lossy compression to reduce the data dynamic range in
an approximately uniform way. Since our NGST simulation is in data
numbers (DN), we must rescale this formula to
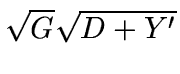 ,
where G is the gain, D is the signal in units of DN and Y'=
R/4G. Therefore, assuming a 15 electrons readout noise and a gain of
4, Y'= 14. (Note R = 152).
,
where G is the gain, D is the signal in units of DN and Y'=
R/4G. Therefore, assuming a 15 electrons readout noise and a gain of
4, Y'= 14. (Note R = 152).
The remaining issue is where to do the truncation. We multiply by a
value NB and round to the nearest integer. The value NB is then
the number of bits into the noise that we save. Setting NB to 1 has
the effect of severely restricting the noise at each pixel but it also
may affect averages and fits that attempt to pull a signal out of the
noise. Larger values of NB allow the compressed data to more
closely match the original values, but at less effective compression
ratios (see RMS Error in Table 1). We suggest using
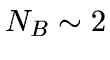 , a value that gets us close to but under the
, a value that gets us close to but under the
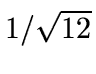 that we could expect from the digitization noise.
Figure 1 shows how this lossy scheme does not introduce
any pattern or systematic error into the residual images. The small
bias shown is due to the digitization process. If this were a problem
in practise, we could add a random bias which will (on average) remove
it.
that we could expect from the digitization noise.
Figure 1 shows how this lossy scheme does not introduce
any pattern or systematic error into the residual images. The small
bias shown is due to the digitization process. If this were a problem
in practise, we could add a random bias which will (on average) remove
it.
Figure 1:
A bright galaxy from a simulated NGST long exposure
(left). Residual plots varying the number of bits into the
noise (right).
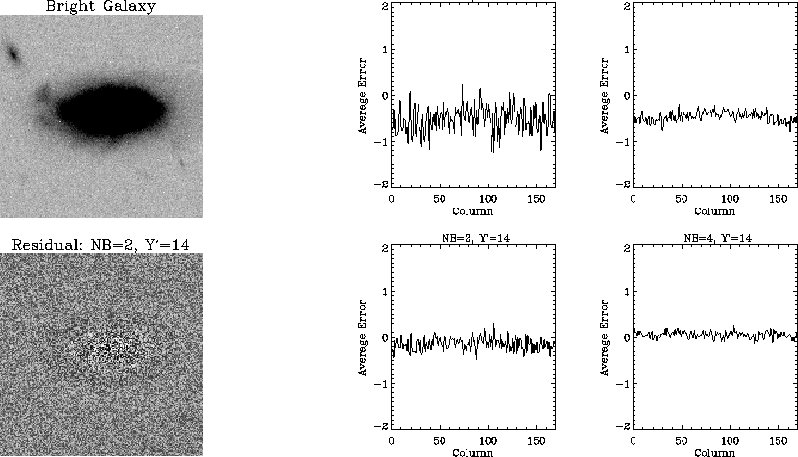 |
For the the maximum exposure time we have adopted, 103 s, it is
expected that  of the image is affected by cosmic rays hits
(Stockman et al. 1998). Most of the cosmic rays produce high values
in one single pixel unrelated to other values in the vicinity. All
tested compression programs benefit from prior cosmic ray removal. The
Rice implementation used in this paper utilizes a linear first-order
unit-delay predictor whose output is equal to the difference between
the input data value and the preceding data value (CCSDS 1997). This
algorithm particularly benefits from CR removal.
of the image is affected by cosmic rays hits
(Stockman et al. 1998). Most of the cosmic rays produce high values
in one single pixel unrelated to other values in the vicinity. All
tested compression programs benefit from prior cosmic ray removal. The
Rice implementation used in this paper utilizes a linear first-order
unit-delay predictor whose output is equal to the difference between
the input data value and the preceding data value (CCSDS 1997). This
algorithm particularly benefits from CR removal.
- It is possible to reduce by more than two orders of magnitude
the anticipated volume of data.
- Our lossy method does not introduce any important distortion
into the data. The prescaling may be very useful for scenes with high
dynamic range, such as 2-D spectra or images of dense star clusters.
- Compression benefits from prior cosmic ray rejection.
- According to the Performance Summary (Table 1)
Rice would be our choice of compression. It is the fastest
algorithm. The bit rates given by Rice are among the best. Current
implementations require the most memory, but this can be improved.
The Consultative Committee for Space Data Systems (CCSDS) recommends
Rice for Lossless Data Compression.
Acknowledgments
The authors thank Rick White for his advice and
letting us use his Rice algorithm implementation. These studies are
supported by the NASA Remote Exploration and Experimentation Project
(REE), which is administered at JPL under Dr. Robert Ferraro, Project
Manager.
References
Consultative Committee for Space Data System 1997, Lossless
Data Compression, (CCSDS120.0-G-1 Green Book), (Washington: NASA)
Offenberg, J. D., Sengupta, R., Fixsen, D. J., Stockman,
P., Nieto-Santisteban, M., Stallcup, S., Hanisch, R., &
Mather, J. C. 1999, this volume, 141
Rice, R. F., Yeh, P.-S., & Miller, W. H. 1993, in
Proc. of the 9th AIAA Computing in Aerospace Conf.,
(AIAA-93-4541-CP), American Institute of Aeronautics and Astronautics
Stiavelli, M. & White, R. L. 1997, STScI Instrument
Science Report, (STScI Publ. ACS-97-02), (Baltimore: STScI)
Stockman, H. S., Fixsen, D. J., Hanisch, R. J.,
Mather, J. C., Nieto-Santisteban, M. A., Offenberg, J. D.,
Sengupta, R. & Stallcup, S. 1998,
astro-ph/9808051
White, R. L. & Becker, I. 1998, in SPIE Proc., Vol. 3356, Space
Telescopes and Instruments V,
ed. P. Y. Bely & J. B. Breckinridge, (Bellingham: SPIE), 823
Footnotes
- ... Fixsen1
- Raytheon STX Corporation, 4400 Forbes Blvd, Lanham, MD 20706
- ... Offenberg2
- Raytheon STX Corporation, 4400 Forbes Blvd, Lanham, MD 20706
© Copyright 1999 Astronomical Society of the Pacific, 390 Ashton Avenue, San Francisco, California 94112, USA
Next: Cosmic Ray Rejection with NGST
Up: Data Compression
Previous: Contour-Based Image Compression for Fast Real-Time Coding
Table of Contents -
Subject Index -
Author Index -
Search -
PS reprint -
PDF reprint
adass@ncsa.uiuc.edu

