Next: Data Retrieval Software for the USNO-A Catalog: Another Member of the -DARES Family
Up: Astrostatistics and Databases
Previous: Background Fluctuation Analysis from the Multiscale Entropy
Table of Contents -
Subject Index -
Author Index -
Search -
PS reprint -
PDF reprint
Murtagh, F. & Starck, J.-L. 1999, in ASP Conf. Ser., Vol. 172, Astronomical Data Analysis Software and Systems VIII, eds. D. M. Mehringer, R. L. Plante, & D. A. Roberts (San Francisco: ASP), 403
A New Entropy Measure Based on Multiple Resolution and
Noise Modeling
Fionn Murtagh
Queen's University Belfast and Strasbourg Observatory
Jean-Luc Starck
CEA, DAPNIA, Saclay
Abstract:
A new measure of information is defined which is based on
noise modeling and incorporates
resolution scale. Properties of this measure are discussed.
Use of such an entropy measure for
filtering and deconvolution is exemplified. Implications
for structuring of, and access to,
image archives are noted.
We show how entropy can be incorporated into a multiscale image processing
setting. The latter is a powerful setting for a wide range of image
processing operations. Additionally it allows for image noise modeling,
and subsequent noise removal.
Immediate applications include image filtering and deconvolution. Other
objectives include object finding and definition, and feature characterization.
More globally, we also note that such vision modeling will be
necessary in future generation image databases.
Background on these methods can be found in Starck, Murtagh, &
Bijaoui (1998).
Information on a multiresolution image and vision software package,
MR/1, can be found at
http://visitweb.com/multires.
The multiscale entropy method consists of measuring
the information h
relative to wavelet coefficients, and of separating this into two parts hs,
and hn. The expression
hs is called the signal information and represents the part
of h which is definitely not contaminated by the noise. The
expression hn is
called the noise information and represents the part
of h which may be contaminated by the noise. We have h = hs+ hn.
Following this notation, the corrected (i.e., filtered) wavelet
or multiscale coefficient 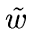 should
minimize:
should
minimize:
i.e. there is a minimum of information in the residual (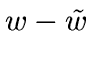 )
due to the significant signal, and a minimum of information
which can be due to the noise in the solution
)
due to the significant signal, and a minimum of information
which can be due to the noise in the solution 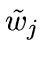 .
.
In order to verify a number of properties, the following functions are
proposed for hs and hn in the case of Gaussian noise:
The regularization parameter, 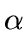 , can be determined by using the
fact that we expect a residual with a given standard deviation at each
scale j equal to the noise standard deviation
, can be determined by using the
fact that we expect a residual with a given standard deviation at each
scale j equal to the noise standard deviation 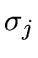 at that
scale. Hence we have an
at that
scale. Hence we have an 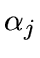 per scale.
per scale.
If we have a model, Dm, for the data we can use
The regularized entropy-based filtering algorithm is as follows.
- Estimate the noise in the data
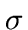 (see Olsen 1993; Starck
& Murtagh 1998a).
(see Olsen 1993; Starck
& Murtagh 1998a).
- Wavelet transform of the data.
- Calculate from
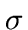 the noise standard deviation
the noise standard deviation 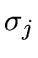 at
each scale j.
at
each scale j.
- Set
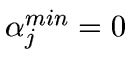 ,
,
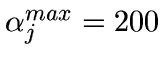 .
.
- For each scale j do
- Set
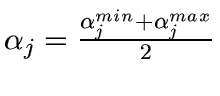
- For each wavelet coefficient wj,k of scale j,
find
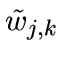 by minimizing
by minimizing
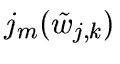 or
or
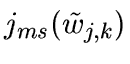
- Calculate the standard deviation of the residual:
- If
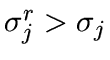 then the regularization is too strong, and
we set
then the regularization is too strong, and
we set
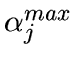 to
to 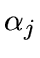 , otherwise we
set
, otherwise we
set
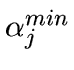 to
to 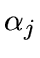 .
.
- If
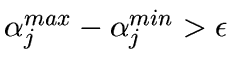 then goto 5.
then goto 5.
- Multiply all
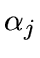 by the constant
by the constant 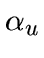 (default: 1).
(default: 1).
- For each scale j and for each wavelet coefficient w
find
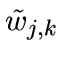 by minimizing
by minimizing
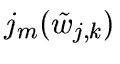 or
or
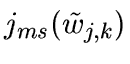 .
.
- Reconstruct the filtered image from
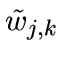 by the
inverse wavelet transform.
by the
inverse wavelet transform.
The minimization of jm or jms (step 5.2) can be done by any method.
For instance,
a simple dichotomy can be used in order to find 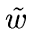 such that
such that
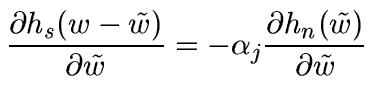 |
|
|
(1) |
The idea to treat the wavelet coefficients
such that the residual respects some constraint has also been used
in Nason (1996) and Amato & Vuza (1998) using cross-validation.
Figure 1 shows a difficult case of smooth and sharp
transitions. The filtering method described here allows an excellent
noise filtering of it to be carried out. Figure 2
shows a spectrum, and an effective noise filtered version.
Figure 1:
Top, noisy blocks and filtered blocks overplotted. Bottom, filtered
blocks.
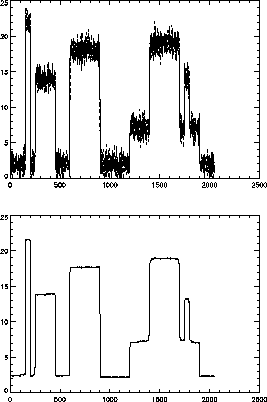 |
Figure 2:
Top, real spectrum and filtered spectrum overplotted.
Bottom, filtered spectrum.
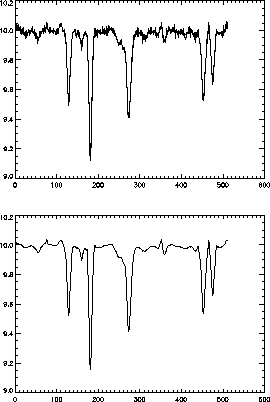 |
We have described an
integrated approach for specification of information content, handling
of noise, and effective implementation.
The multiscale entropy is similarly of benefit in deconvolution.
We note that large image repositories require
- Noise separation, for compression and quicklook
- Variable resolution over time, for progressive transmission, and
variable resolution over space leading to multifoveated images.
- Usable approaches to information characterization.
Hence information- and entropy-based processing technologies will be
necessary for the effective design and implementation of large,
future generation, image databases.
Further reading is available in Starck, Murtagh, & Gastaud (1998)
and Starck & Murtagh (1998b). The methods described here are
available in the multiresolution analysis software package, MR/1, Version
2.0. Details of the MR/1 software package can be
found at http://visitweb.com/multires.
References
Amato, U. & Vuza, D. T. 1998, Rev. Roumaine Math. Pures Appl., in
press
Nason, G. P. 1996, J. Roy. Stat. Soc. B, 58, 463
Olsen, S. I. 1993, Comp. Vis. Graph. Image Proc., 55, 319
Starck, J. L. & Murtagh, F. 1998a, PASP, 110, 193
 , 1998b,
Signal Proc., in press
, 1998b,
Signal Proc., in press
Starck, J. L., Murtagh, F., & Bijaoui, A. 1998, Image and Data
Analysis: The Multiscale Approach, (Cambridge: Cambridge Univ. Press)
Starck, J. L., Murtagh, F. & Gastaud, R. 1998, IEEE Trans. CAS II,
45, 1118
© Copyright 1999 Astronomical Society of the Pacific, 390 Ashton Avenue, San Francisco, California 94112, USA
Next: Data Retrieval Software for the USNO-A Catalog: Another Member of the -DARES Family
Up: Astrostatistics and Databases
Previous: Background Fluctuation Analysis from the Multiscale Entropy
Table of Contents -
Subject Index -
Author Index -
Search -
PS reprint -
PDF reprint
adass@ncsa.uiuc.edu
![]() should
minimize:
should
minimize:
![]() , can be determined by using the
fact that we expect a residual with a given standard deviation at each
scale j equal to the noise standard deviation
, can be determined by using the
fact that we expect a residual with a given standard deviation at each
scale j equal to the noise standard deviation ![]() at that
scale. Hence we have an
at that
scale. Hence we have an ![]() per scale.
per scale.
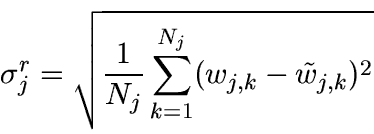
![]() such that
such that
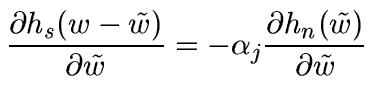
![]() , 1998b,
Signal Proc., in press
, 1998b,
Signal Proc., in press