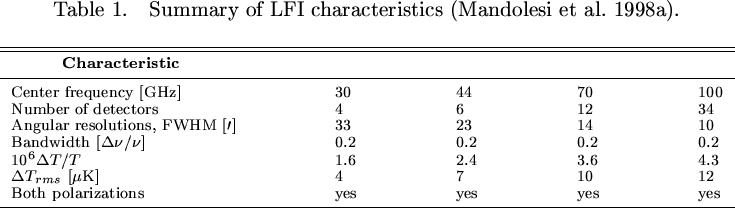
The Planck satellite (formerly COBRAS/SAMBA, Bersanelli et al. 1996), which is planned to be launched in 2007, will produce full sky CMB maps with high accuracy and resolution over a wide range of frequencies. Table 1. summarizes the basic properties of LFI aboard Planck (the reported sensitivities per resolution element, in terms of thermodynamic temperature, represents the goals of LFI for a one-year mission).
The limited bandwidth reserved to the downlink of scientific data calls for huge lossless compression, the theoretical upper limit being a bit less than eight. Careful simulations are demanded to quantify the capability of true compressors for ``realistic'' synthetic data including CMB signal, foregrounds and instrumental noise. An Automated Program Generator was applied to perform this exploratory process by changing the signal components, the dynamic range of detectors and the compression algorithms, which enables to save time, reduce errors and simplify the simulations management.
During the data acquisition phase, the Planck satellite will rotate at
a rate of one circle per minute around a given spin axis that changes
its direction every hour (of 2![]() 5 on the ecliptic plane in the case
of simple scanning strategy), thus observing the same circle on the
sky for 60 consecutive times (Mandolesi et al. 1998a,b). The LFI
instrument will produce continuous data streams of temperature
differences between the microwave sky and a set of onboard reference
sources; both differential measurements and reference source
temperatures must be recorded.
5 on the ecliptic plane in the case
of simple scanning strategy), thus observing the same circle on the
sky for 60 consecutive times (Mandolesi et al. 1998a,b). The LFI
instrument will produce continuous data streams of temperature
differences between the microwave sky and a set of onboard reference
sources; both differential measurements and reference source
temperatures must be recorded.
The data rate will depend on the sampling time,
the present LFI Proposal is ![]() msec for each
detector (Mandolesi et al. 1998a), thus calling
for a typical data rate of
msec for each
detector (Mandolesi et al. 1998a), thus calling
for a typical data rate of ![]() kB/sec,
while the allocated bandwidth for the data is on average only 20 kB/sec.
The data flow have to be downloaded on ground without
information losses, and by minimizing scientific elaboration on board.
The solution of this problem asks for an efficient and lossless compression
of LFI data before they are sent to Earth.
kB/sec,
while the allocated bandwidth for the data is on average only 20 kB/sec.
The data flow have to be downloaded on ground without
information losses, and by minimizing scientific elaboration on board.
The solution of this problem asks for an efficient and lossless compression
of LFI data before they are sent to Earth.
As shown by Gaztñaga et al. (1998), theoretical upper limits for the lossless compression factor of noise data are located between 7.75 and 7.82. On the other hand, such a level of efficiency can be reached under certain optimization hypotheses, it is crucial to study the efficiency of real compression algorithms applied to ``real'' LFI data (as obtained by simulations) in the form of time series. This may lead, as a second step, to the definition of some level of simple ``a priori'' data coding or preprocessing to be performed, aimed at increasing the compression factor by allowing the simulated data to better satisfy the optimization hypotheses. The whole work is aimed at the optimization of the transmission bandwidth dedicated to the downlink of LFI data from the Planck spacecraft to the FIRST/Planck Ground Segment.
For the successful development of the project, the following steps have been identified:
The combination of the above items yields a large number of combinations to be systematically explored. Automatic simulation generation and management through one simplified Automated Program Generator (APG; Maris 1998; Maris & Staniszkis 1999) implementing a Virtual Scanner (VuScanner) under IDL were considered both for analysis and realization. This version of the Virtual Scanner is similar to the MatLab version used for neutrino studies (Maris 1999) with some modifications to take into account the reduced flexibility of the IDL language if compared to MatLab.
Signal detection is simulated through the formula (M. Bersanelli, J. Herrera, & M. Seiffert 1998, private communication)
![]() ,
where V is the detection chain output in Volts (-10V
,
where V is the detection chain output in Volts (-10V
![]() V),
AFO is the detection chain offset (-5V
V),
AFO is the detection chain offset (-5V
![]() V),
VOT is the antenna temperature / voltage conversion factor
(-0.5V/K
V),
VOT is the antenna temperature / voltage conversion factor
(-0.5V/K
![]() V/K),
V/K), ![]() is the difference between
antenna temperatures due to the sky signal and a reference load.
Sixteen bits quantization is applied to the signal before compression
and before writing into a binary file.
is the difference between
antenna temperatures due to the sky signal and a reference load.
Sixteen bits quantization is applied to the signal before compression
and before writing into a binary file.
The output of the compression chain is a set of compression evaluation tables
for the components of the incremental cosmological signal, one for each set of conditions.
The compression efficiency ![]() is evaluated as the ratio
is evaluated as the ratio
![]() ,
where Lu is the uncompressed signal length in bytes and Lc is the compressed signal size.
,
where Lu is the uncompressed signal length in bytes and Lc is the compressed signal size.
We have analyzed the efficiency of four kinds of compression algorithms ( compress, compact, szip and gzip) for a limited sample of the full set of simulations. For these tests, the full range found was 1.9 - 6.5. Our preliminary conclusions are summarized as follows:
In conclusion these realistic compression factors, albeit encouraging as a first result, are about a factor two worse than the theoretical upper limit. Further investigations are required to reach the target compression factor without any on-board data averaging at all. In addition, the choice of a given compressor can not be based only on its efficiency, but also on the on-board available CPU and on the official ESA space qualification: tests with this hardware platform and other compressors will be made. In the near future, long-duration flight balloon experiments will provide a solid base to test and improve compression algorithms.
We warmly acknowledge a number of people which actively support this work, in particular F. Argüeso, M. Bersanelli, L. Danese, G. De Zotti, E. Gaztñaga, J. Herrera, N. Mandolesi, P. Platania, A. Romeo, M. Seiffert and L. Toffolatti for fruitful discussions and K. Gorski, E. Hivon and B. Wandelt for providing us with Healpix pixelisation tools. J.B. acknowledges an INTA grant spent at the OAT in July - August 1998.
Bersanelli, M., et al. 1996, COBRAS/SAMBA, (Rep. Phase A Study, ESA D/SCI(96)3), (Noordwijk: ESA)
Burigana, C., et al. 1997, (TeSRE/CNR Internal Rep., 198/1997)
Burigana, C., et al. 1998, Ap. Lett. Comm., submitted
Gaztñaga, E., et al. 1998, Ap. Lett. Comm. in press
Mandolesi, N., et al. 1998a, ``Low Frequency Instrument for Planck'', Proposal submitted to ESA
![]() , 1998b, Ap. Lett. Comm., submitted
, 1998b, Ap. Lett. Comm., submitted
Maris, M. (ed.) 1998, ``Automated Program Generation at PLANCK/LFI'', PLANCK/LFI Project, http://www.pv.infn.it/ maris/apgatpl.html
Maris, M. 1999, this volume, 50
Maris, M. & Staniszkis, M. 1999, this volume, 470
Seiffert, M., et al. 1997, Rev. of Sci. Instr., submitted