Next: IDL-based Database of Solar Active Regions
Up: Astrostatistics and Databases
Previous: StarView II: A Customizable Query Generation Tool
Table of Contents - Subject Index - Author Index - Search - PS reprint - PDF reprint

Malkov, O., Kovaleva, D., & Schilbach, E. 1999, in ASP Conf. Ser., Vol. 172, Astronomical Data Analysis Software and Systems VIII, eds. D. M. Mehringer, R. L. Plante, & D. A. Roberts (San Francisco: ASP), 387

Application of the Minimum Determination Algorithm to the Study of the Fine Structure in the Mass-Luminosity Relation and of the Nature of ``Overmassive'' Stars

Oleg Malkov, Dana Kovaleva
Institute of Astronomy, 48 Pyatnitskaya St., Moscow 109017, Russia

Elena Schilbach
Astrophysikalisches Institut Potsdam, An der Sternwarte 16, D-14482 Potsdam, Germany

Abstract:

The available observational data on masses and/or luminosities of binary components and the current models for different chemical compositions of Pop I stars were used to improve the mass-luminosity relation for stars of moderate masses. We have developed a technique of simultaneous minimization of the discrepancies between the predicted and observed masses/radii, assuming equal ages and chemical compositions of binary system components. The method of descending coordinates was used to optimize the observed and theoretical parameters.

This technique was also applied to decompose the low-mass components of several stars suspected to be unresolved binaries. In order to explain the offsets of these stars from the ``normal'' location in the mass-luminosity plane, we computed the most probable masses and luminosities of their hidden components.

1. Description of the Method

This paper presents a mathematical approach which can be used in investigations of different astrophysical problems. The method is based on the minimum determination technique applied to functions of several variables covering a limited range of values. Generally, the method can be described as follows.

Let p₁, p₂, ..., p_n be n independently observational parameters (IOP) for a given kind of objects. We assume p⁰₁, p⁰₂, ..., p⁰_n and $\Delta_1, \Delta_2, ..., \Delta_n$ to be their corresponding observed quantities and observational errors, respectively. Further, we define a set of non-directly observable parameters (NDP) q₁, q₂, ..., q_m for the objects under study. In addition, we consider a set of astrophysical conditions relevant for the investigated objects. There are two different kinds of these conditions. First, the strong mathematical relations between parameters p_i = p_i(q₁, ..., q_m, p_j, ..., p_k) (e.g., the mass of a binary is equal to the sum of the component masses); second, the empirical relations between two parameters Q_i = Q_i(q_j) (e.g., mass-luminosity relation).

We define an initial set of parameters (ISP hereafter) selected from NDP and IOP. The remaining parameters from IOP can be computed in accordance with the relations given above. Treating the observational data p⁰_i and their computed values p_i, we can find a new set of ISP which optimally satisfy both the observations and the adopted conditions.

In other words, we have to minimize a function

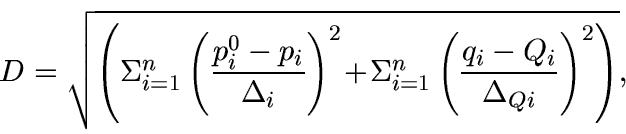$\begin{displaymath} D = \sqrt {\left(\Sigma_{i=1}^n \left(\frac{p^0_i-p_i}{\Delt... ...ma_{i=1}^n \left(\frac{q_i-Q_i}{\Delta_{Qi}}\right)^2\right)}, \end{displaymath}$

(1)

where $\Delta_{Qi}$ is the uncertainty of the relation Q_i = Q_i(q_j).

Minimizing the function D, we can derive optimal sets of IOP and NDP and, consequently, determine more suitable values within their error boxes for observable and non-directly observable parameters. The function D is dimensionless and can be used as a criterion for the accuracy of the solution. To find the minimum of the function D, the method of descending coordinates (or other appropriate numerical algorithms) can be used. An application of the method to a given astrophysical problem assumes a careful construction of the suitable function D and definition of reasonable limits for the included parameters.

Below we present two examples of possible applications.

2. Fine Structure in the Mass-Luminosity Relation

The main objective of the project was to improve the mass-luminosity relation (MLR) for stars of moderate masses by optimal using the available data on binaries components. For this purpose we considered the data (IOP) on masses ( $m^0_1 \pm \Delta(m^0_1), m^0_2 \pm \Delta(m^0_2)$ ) and radii ( $r^0_1 \pm \Delta(r^0_1), r^0_2 \pm \Delta(r^0_2))$ for the components of eclipsing binary stars from the Catalogue of Astrophysical Parameters of Binary Stars (Malkov 1993). The corresponding set of NDP includes the age a ( $\equiv \log T(yr)$ ) and abundance z of the components. Assuming a common origin for the components, we may consider their ages and chemical compositions to be equal. As additional conditions, we used theoretical stellar models of Schaller et al. (1992) for different chemical compositions of Pop I stars. The values of $\lg L$ and $\lg T_{eff}$ derived from these models were used to determine the parameters of the relations r_i = R(m_i, a, z) and the corresponding accuracy $\Delta_{R_i}$ .

The function D to be minimized can be written as

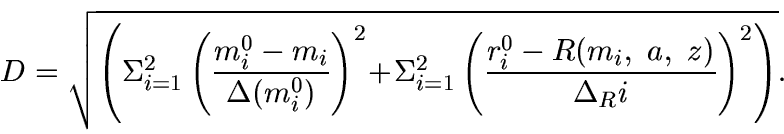$\begin{displaymath} D = \sqrt {\left(\Sigma_{i=1}^2 \left(\frac{m^0_i-m_i}{\Delt... ...2 \left(\frac{r^0_i-R(m_i,~a,~z)}{\Delta_Ri}\right)^2\right)}. \end{displaymath}$

(2)

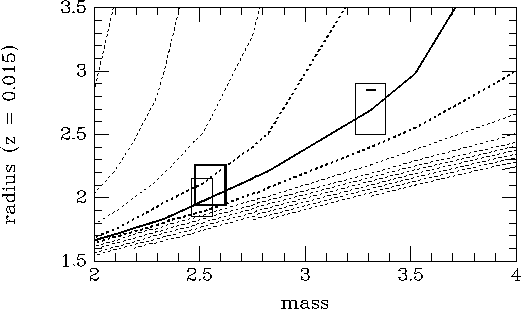
As the result, the optimal values of masses and radii as well as their chemical composition (z) and evolutionary stage (a) were obtained for 12 double star systems. For one of the considered binaries (AS Cam), Fig. 1 shows how these parameters correlate with the original observational data.

**Figure 1:** The IOP of the components of the AS Cam system. The error boxes for the observed (*thin line*) and optimal (*thick line*) values of masses and radii are presented. The isochrones for the optimal abundance z = 0.015 are also plotted in steps of $\Delta a$ = 0.15. The solid line and two heavily dashed lines mark the isochrone of the optimal age of the system and the area of uncertainty ( $a = 8.14 \pm 0.15$ ), respectively.
$\begin{figure} \epsscale{0.7} \plotone{malkovoy2_1.eps} \end{figure}$

About 30 other double star systems are included in the project. Extending the investigations to a larger number of binaries will improve the database on optimal masses and luminosities. This will allow us to derive the mass-luminosity relation for stars of moderate masses with higher accuracy.

3. Explanation of the Nature of ``Overmassive'' Stars

Here we considered stars located in the area of underluminous objects of the MLR. Using the approach described above, we tested whether at least some of them may be considered as photometrically unresolved binaries.

In this case the corresponding IOP are mass m = m₁ + m₂ and luminosity $\lg L = \lg (L_1 + L_2)$ of an underluminous star supposed to be a binary. The initial set of observational data $m^0 \pm \Delta m^0$ , $\lg L^0 \pm \Delta \lg L^0$ for the low mass stars were taken from Malkov, Piskunov, & Shpil'kina (1997). As additional condition, we used the theoretical mass-luminosity relation for the low mass region represented by a function $m=M(\lg L)$ . The width of MLR was assumed to be $\Delta (M) = m * 0.5$ . In this case we have to minimize the function

$\begin{displaymath} D=\sqrt{\left[\frac{m^0-m}{\Delta m^0}\right]^2\!+\! \left[\... ...1}^2 \left[\frac{m_i-M(\lg L_i)}{\Delta(M(\lg L_i))}\right]^2} \end{displaymath}$

(3)

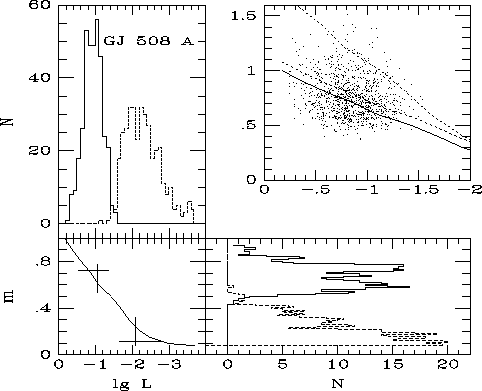
The parameters of components were determined for four recently resolved binaries and for two other stars which have been suspected to be multiple (Kovaleva & Malkov 1999). The distribution of probable values of masses and luminosities is plotted in Fig. 2 for one of the resolved stars (GJ 508 A).

Applying our method to the suspected binaries, we derived the parameters of the components which may describe the situation realistically. Nevertheless, we do not claim that these results present the final proof for the duplicity or multiplicity of these two stars examined here. The offsets of the stars from the usually adopted MLR may be also explained both by large observational errors and by insufficient knowledge of the actual MLR. The results presented here merely show that the possibility for these stars to be unresolved binaries cannot be rejected.

**Figure 2:** Results for the resolved binary GJ 508 A with unknown parameters of the components. The upper right panel presents the MLR (*solid line*) and the binary area (*between the dashed lines*) where the unresolved binaries should be located. Points show the values m and `lg L` which may be accepted for the star due the observational errors. The resulting distributions of masses and luminosities of the main component (*solid lines*) and the secondary component (*dashed lines*) are shown in the lower right and upper left panel, respectively. The predicted masses and luminosities of the components are plotted in the lower left panel together with the theoretical MLR.
$\begin{figure} \plotfiddle{malkovoy2_2.eps}{8cm}{0}{65}{43}{-210}{-55} \end{figure}$

Acknowledgments

The authors thank A. Piskunov and A. Tokovinin for valuable comments. OM and DK acknowledge the Russian Academy of Sciences for the support within the ``Young scientists support program''. OM thanks the Deutsche Forschungsgemeinschaft (project 436 RUS 113/380) and the LOC of the ADASS'98 Conference for the financial support that made this presentation possible.

References

Kovaleva D. A. & Malkov O. Y. 1999, Astronomy Reports, in press

Malkov, O. Y. 1993, Bull. Inf. CDS, 42, 27

Malkov, O. Y., Piskunov, A. E., & Shpil'kina, D. A. 1997, A&A, 320, 79

Schaller G., Schaerer D., Meynet G., Maeder A. 1992 A&AS, 96, 269

adass@ncsa.uiuc.edu