R-Trees for Astronomical Data Indexing

The use of multidimensional spatial access methods (SAMs) has been sometimes advocated in the past for astronomical database applications, in order to speed up the retrieval of data. However, they have had little practical application until now. This can be ascribed partly to the difficulty of integrating new access methods in traditional, i.e., relational, database systems. With the advent of new database management systems, which we call collectively Object Data Management Systems (ODMSs), it is now possible to effectively employ SAMs in building astronomical data management systems. A wide variety of SAMs have been introduced in the past, among these R-trees offer many advantages that make them well suited for astronomical applications. In this paper we describe the features that, in our opinion, make R-trees useful in an astronomical context and how they can be adapted to work with astronomical data.

1. Introduction

The advent of large astronomical databases, particularly catalogues, is posing the problem of giving researchers an efficient and unencumbered access to these large data collections. Finding the answer to this problem has been difficult because traditional database technologies are unable to effectively cope with them (see e.g., Pirenne & Ochsenbein 1991).

The use of multi-dimensional spatial data structures has been advocated to solve this problem, either by building indexes to the main data collection or by physically organizing data on secondary storage media (see e.g., Barrett 1995; Wicenec & Albrecht 1998).

However, it is to be noted that a solution in a database context would be preferable, i.e., we would not like to throw away the advantages brought to us by database technology, in particular query processing and physical and logical data independence.

The recent emergence of new technology databases, that we call collectively ODMSs, now makes it possible to directly support astronomical data and, at least for those system that feature extensible indexing capabilities (Stonebraker 1996), secondary access methods that are natural to these datatypes. However, the question remains about what data structure may be appropriate and/or convenient to index astronomical data.

In this paper we describe the features that in our opinion make R-trees an attractive possibility as indexing structures for astronomical data.

2. R-Trees

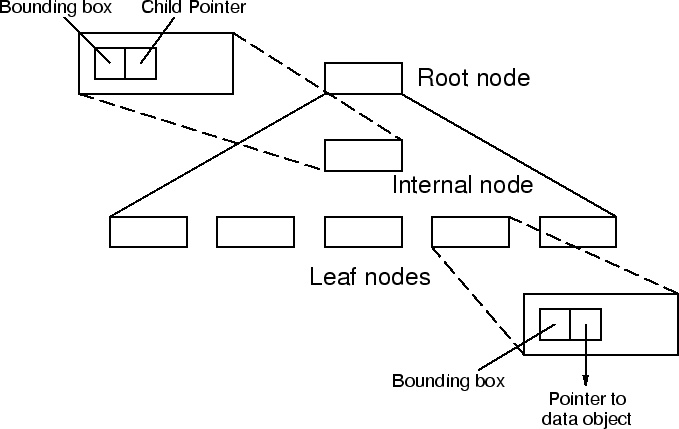
R-trees were originally proposed as an indexing mechanism for non-zero size spatial data in a multi-dimensional Cartesian space (Guttman 1984). Basically, an R-tree is an height-balanced tree in which internal nodes contain couples of pointers to the lower nodes in the tree and the corresponding bounding box, while index records in leaf nodes contain bounding boxes and pointers to the actual data objects. A conceptual representation of an R-tree is shown in Fig. 1. A thorough description of R-trees can be found in the original paper, in this section we concentrate on the issues that, in our opinion, make R-trees interesting for practical implementations of astronomical database management systems.

First of all, although the original definition of R-trees dealt with objects in a Cartesian space and supported only overlap and containment query predicates, it turns out that the basic principle can be generalized to support almost arbitrary data and query predicates (Hellerstein, Naughton, & Pfeffer 1995).

Secondly, besides other spatial search structures that have been proposed in the past and claimed to be more efficient, R-trees are conceptually simple so that they are more easily integrated in a database environment. In fact, they are found both in research (e.g., PostgreSQL, Predator) and commercial DBMSs (e.g., Informix).

Furthermore, there have been many studies aimed at extending R-trees to support parallel (Kamel & Faloutsos 1993a), high concurrency (Kornacker & Banks 1995) and bulk loading (Kamel & Faloutsos 1993b) operations, making this structure particularly attractive for implementation in commercial DBMSs. Although not all these features may be present in the real product, they can in principle be realized.

**Figure 1:** A conceptual view of R-trees.
$\begin{figure} \plotone{baruffoloa1_1.eps} \end{figure}$

One problem with R-trees is that it is not possible to guarantee worst-case performance. However, this is a problem they have in common with almost all other multi-dimensional access methods (Freeston 1995). Experience shows that they nevertheless exhibit good behavior for most kinds of data (Guttman 1984).

Finally it is worth noting that although R-trees were originally intended to index non-zero size spatial data objects, so that bounding boxes are stored in the leaf nodes of the tree, they can obviously index zero-sized objects (points) and a good implementation of this index structure would adapt to make efficient use of disk space (i.e., store points instead of bounding boxes in the leaf pages of the index).

3. Adapting to Astronomical Data

In astronomical data collections, there are many data that can be though of as points in a multi-dimensional space and are then suitable to be indexed using R-trees (i.e., multi-color photometry). Among these, coordinates have always played a special rôle, so that we shortly describe how R-trees can be used to index an astronomical database on them.

Coordinates on the sky can be (and often are) represented in a database as ordered couples of longitude and latitude. An R-tree based index can be built using, in the internal nodes, bounding boxes made up of two coordinate pairs that represent the minimum and maximum latitude and longitude of all objects contained in the branch that is pointed to. Leaf nodes contain the actual coordinates and pointers to the DB records.

With this tree organization, all usual search predicates on coordinates (e.g., point and range query, search by cone) can be applied to the R-trees, provided that proper account is made for the metric (i.e., distance on the sphere), because they are simple variants of the containment and overlap predicates. The same argument applies to nearest neighbor searches for which an algorithm based on R-trees has recently been developed and is general enough to be applied to astronomical coordinates (Roussopoulos, Kelley, & Vincent 1995), in this case also by allowing for the particular metrics on the sphere.

It is worthwhile noting that other representations of coordinates (e.g., by means of triads) and bounding boxes (or, better, bounding predicates, see Wang, Hellerstein, & Lipkind 1998) are possible. In fact, it would be interesting to investigate the various alternatives with respect to disk space requirements and query execution performance.

4. Summary and Conclusions

R-trees, although they may not be the best performing secondary access methods for all data and queries (Kriegel et al. 1990; Wang, Hellerstein, & Lipkind 1998), are convenient to use especially in a database context. This is due to the fact that R-trees based indices, that can be extended to support astronomical data and query predicates, are now found in various research and commercial DBMSs.

Furthermore, advantages over traditional structures (e.g., B-trees) in indexing astronomical data have already been demonstrated in a prototype implementation (Baruffolo & Benacchio 1998a). In fact, we are implementing R-tree based indices in a project aimed at serving a very large on-line Freeston reference catalogue (Baruffolo & Benacchio 1998b; Baruffolo, Benacchio, & Benfante 1999).

References

Baruffolo, A. & Benacchio, L. 1998a, in ASP Conf. Ser., Vol. 145, Astronomical Data Analysis Software and Systems VII, ed. R. Albrecht, R. N. Hook, & H. A. Bushouse (San Francisco: ASP), 382

$\ibid$ , 1998b, in SPIE Proc., Vol. 3349, Observatory Operations to Optimize Scientific Return, ed. P. J. Quinn (Bellingham: SPIE), 274

Barrett, P. 1995, in ASP Conf. Ser., Vol. 77, Astronomical Data Analysis Software and Systems IV, ed. R. A. Shaw, H. E. Payne, & J. J. E. Hayes (San Francisco: ASP), 472

Guttman, A. 1984, Proc. of the SIGMOD'84 Ann. Meet., ed. B. Yormark (Boston: ACM Press), 47

Hellerstein. J. M., Naughton, J. F., & Pfeffer, A. 1995, in Proc. of the 21st Conf. on Very Large Data Bases, ed. U. Dayal, P. M. D. Gray, & S. Nishio (San Francisco: Kaufmann), 562

$\ibid$ , 1993b, in Proc. of the 2nd Intl. Conf. on Information and Knowledge Management, ed. B. Bhargava, T. Finin, & Y. Yesha (New York, ACM Press), 490

Kornacker, M. & Banks, D. 1995, in Proc. of the 21st Conf. on Very Large Data Bases, ed. U. Dayal, P. M. D. Gray, & S. Nishio (San Francisco: Kaufmann), 134

Kriegel, H.-P., Schiwietz, M., Schneider, R., & Seeger, B. 1990, Lecture Notes in CS, 409, 89

Stonebraker, M. 1996, Object-Relational DBMSs: The Next Great Wave, (San Francisco: Kaufmann)

Wicenec, A., & Albrecht, M. 1998, in ASP Conf. Ser., Vol. 145, Astronomical Data Analysis Software and Systems VII, ed. R. Albrecht, R. N. Hook, & H. A. Bushouse (San Francisco: ASP), 512

Wang, S., Hellerstein, J. M., & Lipkind, I. 1998, Near-Neighbor Query Performance in Search Trees, (UCB Tech. Rep. CSD-98-1012)