Next: Constructing and Reducing Sets of HST Observations Using Accurate Spacecraft Pointing Information
Up: Applications
Previous: Realtime, Object-oriented Reduction of Parkes Multibeam Data
using AIPS++
Table of Contents -- Index -- PS reprint -- PDF reprint
R.F. Warren-Smith
Starlink, Rutherford Appleton Laboratory, Chilton, DIDCOT,
Oxon, OX11 0QX, UK
D.S. Berry
Starlink, Department of Astronomy, University of Manchester,
Oxford Road, MANCHESTER, M13 9PL, UK
Writing applications which handle non-linear world coordinate systems (WCS), such as celestial coordinates, in a general way currently presents significant difficulties. Although good algorithms exist to transform between celestial coordinate systems, understanding the relationship between the many different systems in use requires considerable expertise. Storing and retrieving WCS information in datasets also demands familiarity with complicated and changing conventions, such as the many variants of FITS in use. Presenting WCS information graphically (e.g. as coordinate grids) is also algorithmically complex, especially if all-sky plots which include the polar regions must be accommodated.
To address these problems, we have developed a library, AST, which provides a high-level model and programming interface for manipulating WCS data in astronomy. AST stands for `ASTrometry Library', although astrometry is, in fact, only a small part of its function.
Our primary objective has been to insulate programmers from the problems described above by delivering `best practice' solutions in an accessible and flexible form.
AST is designed to be useful in a wide range of software projects and, to this end, dependencies on other software have been minimised (only the widely available SLALIB positional astronomy library is required). AST is implemented in ANSI C for portability. It makes extensive use of object-oriented techniques, but conventional C and FORTRAN77 interfaces are provided -- the latter by an additional C layer (so that only a C compiler is required for building). Provision has been made for new language bindings if needed in future.
Graphical output is via a small group of functions which may easily be implemented over most graphics systems (a PGPLOT implementation is provided). A similar mechanism is used for delivering error messages. This, together with an ability to perform I/O via text and FITS headers, ensures independence of any particular programming environment.
Currently, AST is implemented on PC Linux, Solaris and DEC Unix.
A Mapping does not describe a coordinate system, but merely the inter-relationship between two (unspecified) coordinate systems. It is a `black box' to which coordinate values may be given in return for a set of transformed coordinates. This operation may, in principle, be performed in either direction (the forward and inverse transformations). A Mapping may use any number of input and output coordinates so as to match the, possibly different, dimensionalities of the coordinate systems it inter-relates.
AST provides a selection of different Mappings to support a wide range of celestial coordinate transformations and sky projections. It also provides a range of utility Mappings, such as linear transformations, look-up tables, etc.
An important feature is that any pair of Mappings may be combined together to form a compound Mapping, or CmpMap. A CmpMap is itself a Mapping, so this process may be repeated. In this way, Mappings of arbitrary complexity may be built, giving AST great flexibility in the coordinate transformations it can represent.
While Mappings represent the relationships between coordinate systems, the coordinate systems themselves are represented by objects called Frames. An AST Frame is similar in concept to the frame one might draw around a graph. It contains information about the labels which appear on the axes, the axis units, a title, knowledge of how to format the coordinate values on each axis, etc. A Frame is not, however, restricted to two dimensions and may have any number of axes.
A basic Frame may be used to represent a Cartesian coordinate system
by setting values for its attributes (all AST objects have
attributes which may be set and enquired).
Usually, this would involve setting appropriate axis labels and units,
for example.
Like all objects, a Frame also provides methods.![]() These perform operations such as formatting coordinate values as text,
calculating distances between points, interchanging axes, etc.
These perform operations such as formatting coordinate values as text,
calculating distances between points, interchanging axes, etc.
A derived class, the SkyFrame, is provided to represent celestial coordinate systems, of which a wide range are supported and may be selected by setting appropriate SkyFrame attributes. A SkyFrame provides the additional functionality required when handling celestial coordinates -- such as sexagesimal formatting and great circle distances. It also encapsulates knowledge of how to convert between any pair of celestial coordinate systems, making this available through a method.
As with Mappings (§3), it is possible to merge two Frames together into a compound Frame, or CmpFrame, in which both sets of axes are combined. One could, for example, have celestial coordinates on two axes and an unrelated coordinate (wavelength, perhaps) on a third. Knowledge of the relationship between the axes is preserved internally by the process of constructing the CmpFrame which represents them.
Mappings and Frames may be connected together to form networks called
FrameSets (Figure 1).
One of the Frames in a FrameSet is termed the base Frame. This underlies the FrameSet's purpose, which is to calibrate datasets and other entities by attaching coordinate systems to them. In this context, the base Frame represents the `native' coordinate system (for example, the pixel coordinates of an image). Similarly, one Frame is termed the current Frame and represents the `currently-selected' coordinates. It might, typically, be a celestial coordinate system and would be used during interactions with a user (as when plotting axes on a graph or producing a table of results). Other Frames within the FrameSet represent a library of alternative coordinate systems which a software user can select by making them current.
Graphical output is supported by a specialised class of FrameSet called a Plot. A Plot's base Frame corresponds with the native coordinates of the underlying graphics system. Plotting operations are specified, using AST Plot methods, in physical coordinates which correspond with the Plot's current Frame (typically this might be a celestial coordinate system).
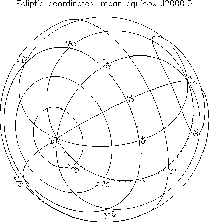
Operations, such as drawing lines, are automatically transformed from physical to graphical coordinates before plotting, using an adaptive algorithm which ensures smooth curves (the transformation is usually non-linear). `Missing' coordinates (e.g. graphical coordinates which do not project on to the celestial sphere), discontinuities and generalised clipping are all consistently handled. It is possible, for example, to plot in equatorial coordinates and clip in galactic coordinates. The usual plotting operations are provided (text, markers), but a geodesic curve replaces the primitive straight line element. There is also a method for drawing axis lines, which are normally not geodesics.
Perhaps the most useful Plot method is for drawing fully annotated
coordinate grids (Figure 2).
 |
Next: Constructing and Reducing Sets of HST Observations Using Accurate Spacecraft Pointing Information
Up: Applications
Previous: Realtime, Object-oriented Reduction of Parkes Multibeam Data
using AIPS++
Table of Contents -- Index -- PS reprint -- PDF reprint