Next: LINNÉ, a Software System for Automatic Classification
Up: Astrostatistics and Databases
Previous: Astrostatistics and Databases
Table of Contents -- Index -- PS reprint -- PDF reprint
Fionn Murtagh (1,2) and Jean-Luc Starck (3)
(1) Faculty of Informatics, University of Ulster, BT48 7JL Derry,
Northern Ireland (e-mail fd.murtagh@ulst.ac.uk)
(2) Observatoire Astronomique, 11 rue de l'Université, 67000 Strasbourg
Cedex, France (e-mail fmurtagh@astro.u-strasbg.fr)
(3) CEA, DSM/DAPNIA, CE-Saclay, 91191 Gif-sur-Yvette Cedex, France
(e-mail jstarck@cea.fr)
Noise is of fundamental importance in astronomy. In practice we must model it. In this article we present a powerful framework for doing this.
Information on the detector's noise properties may be available (Snyder et al. 1993, Tekalp and Pavlovic 1991). In the case of CCD detectors, or digitized photographic images, additive Gaussian and/or Poisson distributions often provide the most appropriate model.
If the noise model is unknown, e.g., due to calibration and preprocessing of the image data being difficult to model, or having images of unknown detector provenance, or in a case where we simply need to check up on our preconceived ideas about the data we are handling, then we need to estimate noise. An algorithm for automated noise estimation is discussed in Starck and Murtagh (1997).
This describes in a
logical or boolean way if an image I contains information at a
given scale j and at a given position (x,y).
If M(I)(j,x,y) = 1 (or ![]() ), then I contains
information at scale j and at the position (x,y).
), then I contains
information at scale j and at the position (x,y).
M depends on several parameters:
The multiresolution support of an image is computed in several steps:
The last step depends on the knowledge we have of our images. E.g., if no interesting object smaller or larger than a given size in our image, we can suppress, in the support, anything which is due to that kind of object.
The à trous algorithm
is described as follows. A pixel at position x,y can be
expressed as the sum all the
wavelet coefficients at this position, plus the smoothed array:
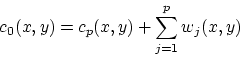 |
(1) |
The multiresolution support
is defined by:
| M(j,x,y) | = 1 | if wj(x,y) is significant | (2) | |
| = 0 | if wj(x,y) is not significant |
Given stationary Gaussian noise,
| (3) | ||
We need the noise standard deviation at each scale for iid (independent identically distributed) Gaussian pixel values. In the case of additive Poisson or Poisson plus Gaussian noise, we transform the image so that this is the case. The transform we use is one for variance stabilization.
To compute the standard deviation ![]() at each scale,
simulate an image containing Gaussian noise with a standard deviation
equal to 1, and take the wavelet transform of this image.
at each scale,
simulate an image containing Gaussian noise with a standard deviation
equal to 1, and take the wavelet transform of this image.
The standard deviation of the noise at a scale j of the image,
![]() , where
, where ![]() is the standard
deviation of the noise in the original image.
is the standard
deviation of the noise in the original image.
If the noise in the data I is Poisson, the transform
| (4) |
For combined Gaussian and Poisson noise:
| (5) |
Reconstruction of the image, after setting non-significant
wavelet coefficients to zero, at full resolution provides an approach for
adaptive filtering. A satisfactory filtering implies
that the error image ![]() , obtained as the difference between
the original image and the filtered image, contains only noise and no
`structure'.
We can easily arrive at this objective by keeping significant wavelet
coefficients and by iterating. The following algorithm
(Starck et al. 1997)
converges quickly to a solution which protects all signal in the image, and
assesses noise with great accuracy.
, obtained as the difference between
the original image and the filtered image, contains only noise and no
`structure'.
We can easily arrive at this objective by keeping significant wavelet
coefficients and by iterating. The following algorithm
(Starck et al. 1997)
converges quickly to a solution which protects all signal in the image, and
assesses noise with great accuracy.
A simulated image containing stars and galaxies is shown in Figure 1 (top left). The simulated noisy image, the filtered image and the residual image are respectively shown in Figure 1 top right, bottom left, and bottom right. We can see that there is no structure in the residual image. The filtering was carried out using the multiresolution support.
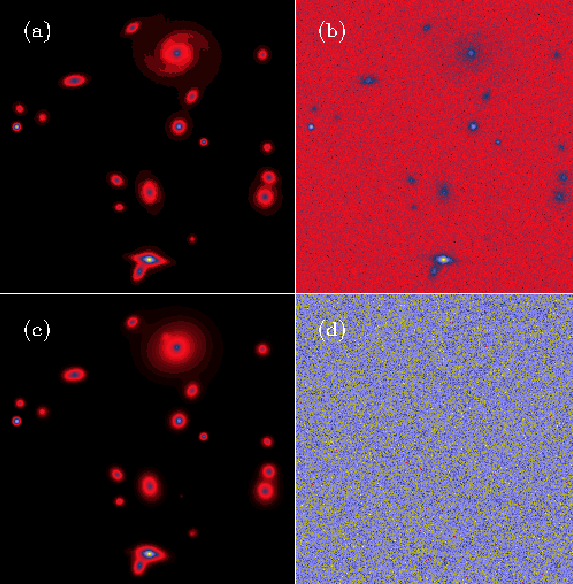 |
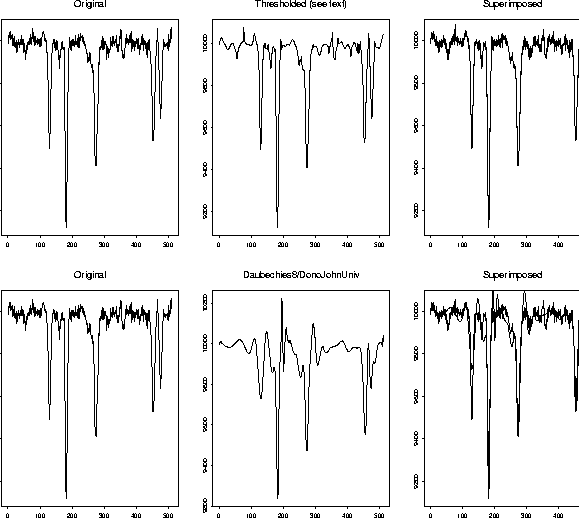
Figure 2 shows a noisy spectrum (upper left, repeated
lower right). For
the astronomer, the spectral lines - here mainly absorption lines extending
downwards - are of interest. The continuum may also be of interest, i.e. the overall spectral tendency.
The spectral lines are unchanged in the filtered version (upper center, and upper right). The lower center (and lower right) version shows the result of applying Daubechies' coefficient 8, a compactly-supported orthonormal wavelet. This was followed by thresholding based on estimated variance of the coefficients, as proposed by Donoho (1990), but not taking into account the image's noise properties as we have done. One sees immediately that a problem- (or image-) driven choice of wavelet and filtering strategy is indispensable.
 |
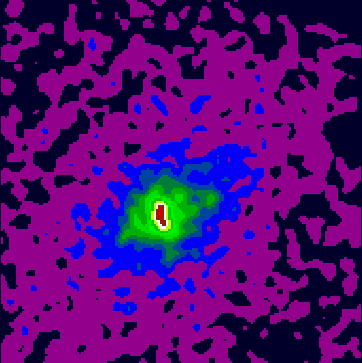
The galaxy cluster A2390 is at a redshift of 0.231.
Figure 3 shows an image of this cluster,
obtained by the ROSAT X-ray spacecraft. The resolution is one arc second
per pixel, with a total number of photons equal to 13506 for an
integration time of 8.5 hours. The background level
is about 0.04 photons per pixel.
It is obvious that this image
cannot be used directly, and some treatment must be performed before
any analysis. The standard method consists of convolving the image
with a Gaussian. Figure 4 shows the result of
such processing. (The Gaussian used had full-width at half maximum
equal to 5", which is approximately that of the point spread function).
The smoothed image shows some structures, but also residual noise,
and it is difficult to give any meaning to them.
Figure 5 shows an image filtered by the wavelet transform (Starck and Pierre 1997a). The noise has been eliminated, and the wavelet analysis indicates faint structures in X-ray emission, allowing explanation of gravitational amplification phenomena, observed in the visible domain (Starck and Pierre 1997b).
 |
The methods described in this article have been applied to many practical problems over the last few years. A comprehensive treatment of these methods can be found in Starck et al. (1998). A large software package will be available from early 1998.
Donoho, D.L. & Johnstone, I.M. 1993, ``Ideal spatial adaptation by wavelet shrinkage'', Stanford University, Technical Report 400 (available by anonymous ftp from ftp://playfair.stanford.edu/pub/donoho)
Snyder, D.L., Hammoud, A.M. and White, R.L. 1993, J. Optical Soc. Am. 10, 1014
Starck, J.-L. Murtagh, F. & Bijaoui, A. 1998, Image and Data Analysis: the Multiscale Approach, Cambridge University Press, in press
Starck, J.-L. & Murtagh, F. 1997, ``Automatic noise estimation from the multiresolution support'', PASP, in press
Starck, J.-L. & Pierre, M. 1997a, ``X-ray structures in galaxy cores'', to appear in A&A
Starck, J.-L. & Pierre, M. 1997b, ``Structure detection in low intensity X-ray images'', to appear in A&A
Tekalp, A.M. and Pavlovic, G. 1991, in A.K. Katsaggelos, ed., Digital Image Restoration, Springer-Verlag, New York, 209
Next: LINNÉ, a Software System for Automatic Classification
Up: Astrostatistics and Databases
Previous: Astrostatistics and Databases
Table of Contents -- Index -- PS reprint -- PDF reprint