Next: Modelling Spectro-photometric Characteristics of
Eclipsing Binaries
Up: Computational Astrophysics
Previous: Modelling Spectro-photometric Characteristics of Nonradially Pulsating Stars
Table of Contents -- Index -- PS reprint -- PDF reprint
E. Grocheva and A. Kiselev
Photographic Astrometry Department, Pulkovo Observatory,
S.Petersburg, 196140, Russia, Email: gl@spb.iomail.lek.ru
We shall present methods which allow the identification of physical binary stars in a probabilistic sense. The application of probability theory provides a more complete picture of the frequency of stellar binarity than simple methods based only on proximity or proper motion. We will also present preliminary results from the application of these methods to Pulkovo's observation program of binary star systems, and outline how such methods might be applied to present and future high precision astrometric catalogues.
We propose to use the real distribution of proper motions for estimation of P. Let the probability of
finding the primary component in the area ![]() equal 1 as a probability of a reliable
event. The probability P of finding n components in a small area
equal 1 as a probability of a reliable
event. The probability P of finding n components in a small area ![]() may be represented as:
may be represented as:
| |
(1) |
where
![]() - probability of finding n stars in small area limited with angular distance
- probability of finding n stars in small area limited with angular distance ![]() for the case of
a random distribution, (Deutsch,1962):
for the case of
a random distribution, (Deutsch,1962):
| |
(2) |
n - is multiplicity of a star system;
![]() - is area where N stars are randomly disposed;
- is area where N stars are randomly disposed;
![]() - probability of the proximity of proper motions
- probability of the proximity of proper motions ![]() and
and ![]() ;
;
![]() - error of determination of proper motions.
- error of determination of proper motions.
Let ![]() be a random vector,
be a random vector, ![]() , where
, where ![]() ,
, ![]() . If
. If ![]() takes on a value from the cell
takes on a value from the cell
![]() , then we say
that random vector
, then we say
that random vector ![]() takes the value
takes the value ![]() . Hence, vector
. Hence, vector ![]() may take the
following values:
may take the
following values:
![]()
p11,p12,..,pnn.
and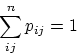
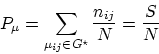 |
(3) |
where ![]() is the Borel's set,
where the tips of vectors are situated at:
is the Borel's set,
where the tips of vectors are situated at:
| (4) |
Now we will describe a procedure for the solution of this problem without a concrete realisation.
![]()
The distribution of proper motions was derived from the PPM catalogue for stars of the North-polar
area. The parameters of the distributions are in Table 1. The predominance of negative motions, especially of ![]() , is readily observable. This is due to the location of the North-polar area relative to the Solar apex.
We chose 76 double stars from Pulkovo's observation program and
calculated the probabilities of a random distribution for these pairs. There are 8 physical and 12 optical
systems among them (Grocheva,1996 & Catalogue of relative positions
and motions of 200 visual double stars,1988).
The proper motions of these pairs was obtained by using the catalogue
``Carte du Ciel'' and modern observations with the 26''refractor. The precision of
, is readily observable. This is due to the location of the North-polar area relative to the Solar apex.
We chose 76 double stars from Pulkovo's observation program and
calculated the probabilities of a random distribution for these pairs. There are 8 physical and 12 optical
systems among them (Grocheva,1996 & Catalogue of relative positions
and motions of 200 visual double stars,1988).
The proper motions of these pairs was obtained by using the catalogue
``Carte du Ciel'' and modern observations with the 26''refractor. The precision of ![]() is 0''.005
/yr.
is 0''.005
/yr.
| Mean | Variance | max | min | ||
| -0''.0006 | 0.047 | 1''.545 | -2''.97 | ||
| -0''.0059 | 0.041 | 0''.818 | -1''.74 | ||
Analysing the resulting probabilities we conclude that only the
probability of random
proximity of proper motions ![]() can be used to identify true physical binaries. Multiplication
can be used to identify true physical binaries. Multiplication
![]() by
by ![]() corrupts the probability pattern. Figure 1 shows
probabilities
corrupts the probability pattern. Figure 1 shows
probabilities ![]() on a logarithmic scale (we numbered the pairs of this sample
from 1 to 76 and used these numbers as x-coordinates). We see that probabilities for physical pairs are less than
0.01, whilst those for optical ones are large. Hence, the quantity
on a logarithmic scale (we numbered the pairs of this sample
from 1 to 76 and used these numbers as x-coordinates). We see that probabilities for physical pairs are less than
0.01, whilst those for optical ones are large. Hence, the quantity
![]() may be used to identify
physical binaries and the limit of probability of proper motions proximity S/N is 0.01 for
physical pairs. It turned out that only 27 physical binaries were among the sample of 76
double stars.
may be used to identify
physical binaries and the limit of probability of proper motions proximity S/N is 0.01 for
physical pairs. It turned out that only 27 physical binaries were among the sample of 76
double stars.
The technique presented identifies physical binaries. This method has a simple algorithm and can be used for the automatic treatment of large stellar catalogues. We are pleased to also note that this method requires only minimal data such as positions and proper motions. This method was used to correct the Pulkovo's program of binary star observations.
Deutsch, A. N., 1962, ``The visual double stars''. in The course of astrophysics and stellar astronomy, p.60, Moscow, (in Russian).
Catalogue of relative positions and motions of 200 visual double stars.,1988, Saint-Petersburg, (in Russian).
Grocheva, E. A., 1996, ``Physical and optical double stars...'', Workshop The Visual Double Stars.., Spain.
Aitken, R. G., 1932, New General Catalogue of Double Stars, Edinburgh
Next: Modelling Spectro-photometric Characteristics of
Eclipsing Binaries
Up: Computational Astrophysics
Previous: Modelling Spectro-photometric Characteristics of Nonradially Pulsating Stars
Table of Contents -- Index -- PS reprint -- PDF reprint