 |
Next: Pipeline Calibration for STIS
Up: Dataflow and Scheduling
Previous: HST Paper Products: A New Way to Look at HST Data
Table of Contents -- Index -- PS reprint -- PDF reprint
J.-P. De Cuyper and H. Hensberge
Royal Observatory of Belgium, Ringlaan 3, B-1180 Brussel, Belgium
Nowadays it is not unusual for the knowledge about an instrument acquired by the design and construction team to be only partially transmitted to those developing the data reduction software or operating the instrument; the feedback to the observer is still smaller. This may result in confusion about basic instrumental parameters, the precision of the set-up, the amount and distribution of calibration frames which are required and finally the assumptions on which the data reduction procedure should rely. The data set then does not deliver the precision aimed at during observing, or observing time was spent inefficiently. The concept of pipeline reductions and on-line controlled operation of the instrument and of the observational procedure offer unprecedented possibilities for delivering data with known error characteristics, provided that the instrumental design, the set-up, the calibration and the data reduction procedure are tuned to each other at a consistent level of accuracy. Our experience with echelle spectroscopy indicates that, as a visiting astronomer, it is impossible to collect the information needed to obtain this goal. Moreover, it is not at all evident to what extent forthcoming pipelines will include realistic error estimates (in addition to random noise estimates).
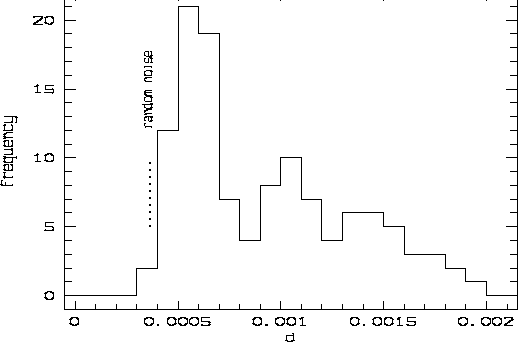
The results shown here refer to two adjacent series of eight consecutively taken flat-fields (tungsten lamp exposures). The telescope was in the zenith and tracking was off. The analysis method applied is insensitive to global changes in intensity and to small changes in location, width or shape of the cross-order profile (these changes are below 0.5% in intensity and within 0.02 pix for the other quantities in both series). For each pair of frames, a parameter d indicating the lack of similarity in the shape of the blaze profile was computed (Figure 1). It turns out that the excess of d over its value calculated from the case of random noise can be modelled as a ``distance'' between frames (Figure 2).
 |
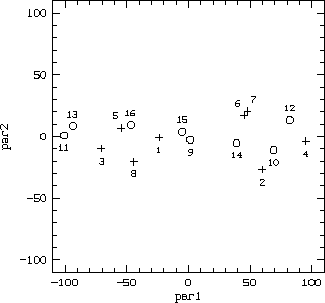 |
The lack of repeatability in subsequent frames is due to instabilities that
grow and disappear, rather than to a slow, continuous change with time.
Consecutively
taken frames differ more than the ones separated by an intermediate frame,
and the global pattern of changes repeats in the two independent series
(Figure 2). Relative deformations in the shape of the blaze
profile appear over several spectral orders in the same set of rows
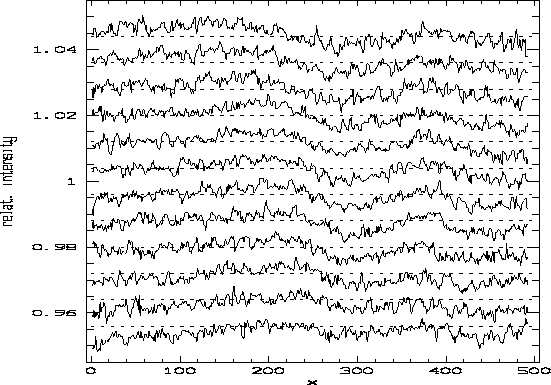
of the detector (see e.g., Figure 3 near ![]() ).
).
It is not our intention to show that things can sometimes go very wrong, but merely that the accuracy is generally limited by systematic errors. The example shown above does not refer to an exceptional malfunctioning, but to a common situation. Notice that it is not uncommon to detect stronger effects when comparing exposures taken with longer time delays and/or in different telescope positions. The detectability of such systematic effects sets a natural limit on the precision of order merging (since the intensity ratio of the wavelength overlap region of consecutive orders is affected), on the level up to which faint, shallow spectral features can be trusted and on the precision of the continuum placement.
 |
Experience with echelle spectroscopy confirms that the previous example is not an isolated case of bias. Systematic errors are detectable in almost all types of frames and they influence directly the applicability and the accuracy of the data reduction algorithms. Depending on the ratio of systematic to random noise, algorithms that are based on the dominance of random noise (such as the detection of radiation events, the application of optimal extraction and any reduction step involving non-robust least-squares fitting) may need refinements.
Rather than commenting on specific sources of bias, we like to outline a procedure, interconnecting the different phases from instrument development and testing to data reduction software development, that in our opinion would permit the user to evaluate properly the quality of the final data with regard to the particular aspects of interest to his/her specific purpose:
This research was carried out in the framework of the project `IUAP P4/05' financed by the Belgian Federal Scientific Services (DWTC/SSTC). We thank W. Verschueren (RUCA, University of Antwerp), who obtained the calibration spectra discussed in this paper, and H. Van Diest for help with the data handling. This work is based on observations obtained at the European Southern Observatory (ESO), La Silla, Chile.
Next: Pipeline Calibration for STIS
Up: Dataflow and Scheduling
Previous: HST Paper Products: A New Way to Look at HST Data
Table of Contents -- Index -- PS reprint -- PDF reprint