Next: Identification and Analysis of Binary Star Systems using Probability Theory
Up: Computational Astrophysics
Previous: Parallel Tree N-body Code: Data Distribution and DLB on the CRAY T3D
for Large Simulations
Table of Contents -- Index -- PS reprint -- PDF reprint
Jadwiga Daszynska and Henryk Cugier
Astronomical Institute of the Wroclaw University
PL-51-622 Wroclaw, ul. Kopernika 11, Poland
For a given mode of oscillation the harmonic time dependence,
exp(i![]() ), and spherical harmonic horizontal dependence,
), and spherical harmonic horizontal dependence,
![]() , are assumed for the first order perturbed
quantities. The mass displacement for the spheroidal modes
is described by y- and z-eigenfunctions and for toroidal modes
by
, are assumed for the first order perturbed
quantities. The mass displacement for the spheroidal modes
is described by y- and z-eigenfunctions and for toroidal modes
by ![]() -eigenfunctions, cf. Dziembowski & Goode (1992).
In the case of slowly rotating stars one can use the zero-rotation
approximation to describe stellar pulsations.
Such a model was used already by Cugier, Dziembowski & Pamyatnykh (1994)
to study nonadiabatic observables of
-eigenfunctions, cf. Dziembowski & Goode (1992).
In the case of slowly rotating stars one can use the zero-rotation
approximation to describe stellar pulsations.
Such a model was used already by Cugier, Dziembowski & Pamyatnykh (1994)
to study nonadiabatic observables of ![]() Cephei stars.
Apart from ynlm(r) and znlm(r) it is desirable to use
the eigenfunction pnlm(r), connected with the Lagrangian perturbation
of pressure, and the fnlm(r)-eigenfunction, which describes the variations
of the local luminosity.
In the nonadiabatic theory of pulsation the eigenvalues
Cephei stars.
Apart from ynlm(r) and znlm(r) it is desirable to use
the eigenfunction pnlm(r), connected with the Lagrangian perturbation
of pressure, and the fnlm(r)-eigenfunction, which describes the variations
of the local luminosity.
In the nonadiabatic theory of pulsation the eigenvalues ![]() and the eigenfunctions are complex (cf. e.g., Dziembowski 1977) and
and the eigenfunctions are complex (cf. e.g., Dziembowski 1977) and
![]() is the phase lag between
the light and radius variations.
is the phase lag between
the light and radius variations.
The monochromatic flux of radiation is given by
![]()
In the program the specific intensity data for the new generation
line-blanketed model atmospheres of Kurucz (1996) were used in order to study
the continuum flux behaviour and photometric indices.
Kurucz's (1994) data contain monochromatic fluxes for
1221 wavelengths and monochromatic intensities at 17 points of
![]() .Using these data one can interpolate the monochromatic intensities
for the local values of
.Using these data one can interpolate the monochromatic intensities
for the local values of ![]() ,
, ![]() and
and ![]() .We can also introduce the linear or quadratic shape for the limb-darkening
law as defined by Wade & Rucinski (1985).
.We can also introduce the linear or quadratic shape for the limb-darkening
law as defined by Wade & Rucinski (1985).
Integrating Eq.1 over the surface in the linear approach we can obtain the semi-analytical solution, cf. Daszynska & Cugier (1997) for details,
![\begin{displaymath}
\frac{\Delta{\cal F}_{\lambda}}{{\cal F}_{\lambda}^0} =
\va...
...
+ (T_3 +T_4 +T_5) \cos (\omega_{nlm} -m\Omega)t \Big].\eqno(2)\end{displaymath}](img24.gif)
We examined how the results are influenced by different methods of integration over the stellar surface. The following cases were considered:
- Model 1: the semi-analytical method (Eq.2) with the quadratic form for the limb-darkening law,
- Model 2: the numerical integration of Eq.1 with the quadratic form for the limb-darkening law; constant limb-darkening coefficients corresponding to the equilibrium model were assumed,
- Model 3: the same as Model 2, but the limb-darkening coefficients were
interpolated for local values of ![]() and
and ![]() ,
,
- Model 4: numerical integration over stellar surface with specific
intensities interpolated for the local values
of ![]() ,
, ![]() and
and ![]() .
.
As an example we consider the energy flux distribution and nonadiabatic
observables for a ![]() Cep model. We chose the stellar model
(
Cep model. We chose the stellar model
(![]() = 4.33668,
= 4.33668, ![]() = 4.07842) calculated with OPAL
opacities. This model shows unstable l = 0, 1 and 2 modes of oscillations.
We calculated theoretical fluxes and the corresponding Strömgren
photometric indices at pulsating phases
= 4.07842) calculated with OPAL
opacities. This model shows unstable l = 0, 1 and 2 modes of oscillations.
We calculated theoretical fluxes and the corresponding Strömgren
photometric indices at pulsating phases ![]() = 0.05 n (n=0,...,20).
Subsequently amplitudes and phases of the light curves were computed by
the least-square method. The accuracy of these calculations can be estimated
from Table 1, which gives the results for the Models 1 - 4.
The calculations were made on Sun Ultra 1 (192 MB RAM, 166 MHz) computer.
The CPU time per 1 pulsating stellar model is from about 2 seconds
(for Model 1) to about 10 hours (for Model 4).
= 0.05 n (n=0,...,20).
Subsequently amplitudes and phases of the light curves were computed by
the least-square method. The accuracy of these calculations can be estimated
from Table 1, which gives the results for the Models 1 - 4.
The calculations were made on Sun Ultra 1 (192 MB RAM, 166 MHz) computer.
The CPU time per 1 pulsating stellar model is from about 2 seconds
(for Model 1) to about 10 hours (for Model 4).
| l | 1cAy* | Au/Ay | |||||
| Model 1 | 0.0211 | 3.3166 | 2.0024 | -0.0381 | 0.8241 | -0.0701 | |
| Model 2 | 0.0211 | 3.3167 | 2.0000 | -0.0381 | 0.8220 | -0.0715 | |
| Model 3 | 0.0213 | 3.3167 | 2.0000 | -0.0381 | 0.8220 | -0.0715 | |
| Model 4 | 0.0211 | 3.3168 | 2.0000 | -0.0381 | 0.8217 | -0.0718 | |
| Model 1 | 1 | 0.0207 | 3.1916 | 1.5958 | 0.0004 | 0.4876 | 0.0038 |
| Model 2 | 1 | 0.0268 | 3.1929 | 1.6119 | 0.0002 | 0.4975 | 0.0022 |
| Model 3 | 1 | 0.0268 | 3.1929 | 1.6112 | 0.0002 | 0.4975 | 0.0022 |
| Model 4 | 1 | 0.0222 | 3.1910 | 1.5526 | 0.0009 | 0.4535 | 0.0048 |
| Model 1 | 2 | 0.0204 | 3.2077 | 1.3476 | 0.0164 | 0.2560 | 0.0790 |
| Model 2 | 2 | 0.0195 | 3.2083 | 1.3457 | 0.0161 | 0.2568 | 0.0801 |
| Model 3 | 2 | 0.0195 | 3.2083 | 1.3457 | 0.0161 | 0.2568 | 0.0801 |
| Model 4 | 2 | 0.0077 | 3.2084 | 1.3170 | 0.0160 | 0.2459 | 0.0804 |
| *assumed |
The velocity field of pulsating stars may be found by calculating the time derivative of the Lagrangian displacement. Including the first order effect, the radial component vp as seen by a distant observer is:
![]()
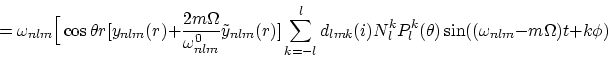
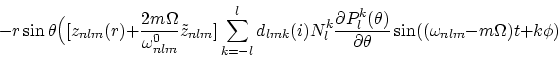
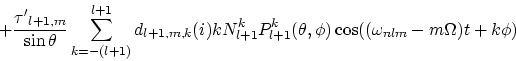
![\begin{displaymath}
+ \frac {{\tau'}_{l-1,m}}{\sin\theta} \sum_{k=-(l-1)}^{l-1}
...
...i)
\cos((\omega_{nlm} -m\Omega) t+k\phi) \Big) \Big]. \eqno(3)\end{displaymath}](img33.gif)
![]()
We illustrate the predicted behaviour of Si III 455.262 nm
line profiles for stellar model given in Sect.3.
We considered Kurucz's (1994) model atmospheres with the solar chemical
composition and the microturbulent velocity ![]() = 0.
All calculations were made for the amplitude of the stellar
radius variations
= 0.
All calculations were made for the amplitude of the stellar
radius variations ![]() and rigid rotation.
Figures 1a-f show the theoretical line profiles for
different phases of pulsation for
and rigid rotation.
Figures 1a-f show the theoretical line profiles for
different phases of pulsation for ![]() and the equatorial
velocity
and the equatorial
velocity ![]() . The spectra are given
in absolute units. In order to avoid overlap, vertical offsets
were added to each spectrum using the relationship:
. The spectra are given
in absolute units. In order to avoid overlap, vertical offsets
were added to each spectrum using the relationship:
![]() .
.
This work was supported by the research grant No.2 P03D00108 from the Polish Scientific Research Committee (KBN).
Cugier, H., Dziembowski W. A., & Pamyatnykh A. A. 1994, A&A, 291, 143
Daszynska J., & Cugier H. 1997. submitted for publication
Dziembowski W. A. 1977, Acta Astron. 27, 95
Dziembowski W. A., & Goode P. R. 1992, ApJ, 394, 670
Kurucz R. L. 1994, CD-ROM No.19
Kurucz R. L. 1996, private communication
Wade R. A., & Rucinski S. M. 1985, A&AS, 60, 471
Next: Identification and Analysis of Binary Star Systems using Probability Theory
Up: Computational Astrophysics
Previous: Parallel Tree N-body Code: Data Distribution and DLB on the CRAY T3D
for Large Simulations
Table of Contents -- Index -- PS reprint -- PDF reprint