Next: Image Processing of Digitized Spectral Data
Up: Applications
Previous: The IRAF Mosaic Data Reduction Package
Table of Contents -- Index -- PS reprint -- PDF reprint
Michail I. Agafonov
Radiophysical Research Institute (NIRFI), 25 B.Pecherskaya st.,
Nizhny Novgorod, 603600, Russia, E-mail: agfn@nirfi.nnov.su
Iterative algorithms with non-linear constraints are very attractive in image reconstruction with only a few strip-integrated projections (Vasilenko & Taratorin 1986). The process of convergence to solutions for the various realizations of iterative schemes using the different versions of the CLEAN algorithm have already been investigated for this problem (Agafonov & Podvojskaya 1989). Two dimensional image reconstruction from 1-D projections is often hampered by the small number of available projections, by an irregular distribution of position angles, and by positions angles that span a range smaller than about 80 degrees. These limitation are typical of both lunar occultations of celestial sources and observations with the fan beam of radio telescope, and also apply to greatly foreshortened reconstructive tomography. Our previous paper (Agafonov 1997) also contains the basic description of the problem and the features of 2-CLEAN DSA method. This paper contains some examples and useful diagrams and also a valuable addition for the development of the reconstruction technique for this problem.
The problem requires the solution of the equation
| (1) |
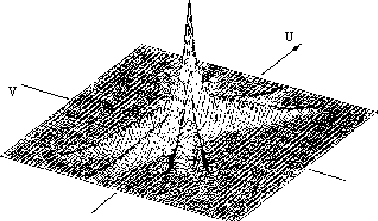 |
A two dimensional image reconstruction of a complicated object using a poor fan beam function H(u,v) needs to carry out the following procedure:
 |
 |
CLEAN forms the solution from the sum of peaks and the result is the sharpest variant permissible within the established constraints. On the other hand TC-CLEAN accumulates its result from the most extended components that satisfy the constraints, producing the smoothest solution (Agafonov & Podvojskaya 1990).
A simple object (consisting of the peaks) may be successfully restored
by the standard CLEAN. The results obtained by both methods
are practically identical for a simple object consisting of individual
components, but TC-CLEAN is more computationally efficient. For smoothed
1-D profiles with small ``hillocks", the solution can be
obtained from the isolated individual components (CLEAN), and also
from the more smoothed components (TC-CLEAN). CLEAN increases the
contrast of small components, but the extended background decreases
because of ``grooves".
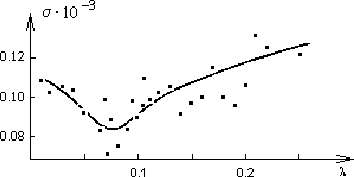
If ![]() (CLEAN)
(CLEAN) ![]() (TC-CLEAN) (see the example shown in Figures 3 and 4),
the solutions will be formally equivalent for both algorithms,
and so we have two choices: (i) to prefer the result corresponding
to the physical peculiarities of the object in accordance with
(TC-CLEAN) (see the example shown in Figures 3 and 4),
the solutions will be formally equivalent for both algorithms,
and so we have two choices: (i) to prefer the result corresponding
to the physical peculiarities of the object in accordance with ![]() information; or (ii) to assume the existence a probable class
of solutions between the ``smooth" one from TC-CLEAN and the ``sharp"
one from CLEAN.
information; or (ii) to assume the existence a probable class
of solutions between the ``smooth" one from TC-CLEAN and the ``sharp"
one from CLEAN.
The area of permissible solutions of complicated
objects can be determined with a help of both algorithms.
The 2-CLEAN DSA procedure can show a range of possible images
from ``smooth" to ``sharp" variants satisfying
imposed constraints and poor ![]() information.
information.
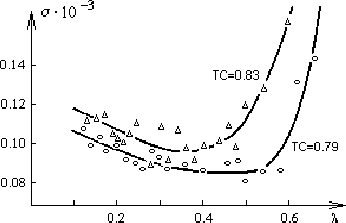
The application of TC-CLEAN and CLEAN was presented as a
reconstruction of the Crab Nebula map at 750 MHz
(Agafonov et al. 1990). The method of 2-CLEAN DSA allowed us
to determine that the area of the permissible solutions lies
formally between the ``sharp" (CLEAN) and ``smooth" (TC-CLEAN) variants.
Two maps were generally similar. The standard CLEAN increased the
contrast of small components while the TC-CLEAN map gave a better
agreement with known ![]() information.
information.
I am grateful to the Space Telescope European Coordinating Facility and European Southern Observatory for the support which made possible this presentation and my special gratitude to Rudi Albrecht, Richard Hook and Britt Sjoeberg for their attention and endurance.
Agafonov, M. I. 1997, in Astronomical Data Analysis Software and Systems VI, ASP Conf. Ser., Vol. 125, eds. Gareth Hunt and H. E. Payne (San Francisco, ASP), 202
Agafonov, M. I., & Podvojskaya, O. A. 1989, Izvestiya VUZ. Radiofizika, 32, 742
Agafonov, M. I., & Podvojskaya, O. A. 1990, Izvestiya VUZ. Radiofizika, 33, 1185
Agafonov, M. I., Ivanov, V. P., & Podvojskaya, O. A. 1990, AZh, 67, 549
Bracewell, R. N., & Riddle, A. C. 1967, ApJ, 150, 427
Hogbom, J. A. 1974, A&AS, 15, 417
Steer, D. G., Dewdney, P. E., & Ito, M. R. 1984, A&A, 137, 159
Vasilenko, G. I., & Taratorin A. M. 1986, Image Restoration (in Russian), Radio i svyaz', Moscow.
Next: Image Processing of Digitized Spectral Data
Up: Applications
Previous: The IRAF Mosaic Data Reduction Package
Table of Contents -- Index -- PS reprint -- PDF reprint