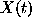 is a stationary stochastic
process with zero mean defined by a set of realizations
is a stationary stochastic
process with zero mean defined by a set of realizations
Next: A New Stable Method for Long-Time Integration in an N-Body Problem
Previous: Time Series Analysis of Unequally Spaced Data: Intercomparison Between Estimators of the Power Spectrum
Up: Algorithms
Table of Contents - Index - PS reprint - PDF reprint
V. V. Vityazev
Astronomy Department, St. Petersburg University, Bibliotechnaya pl.2,
Petrodvorets, St. Petersburg, 198904, Russia.
Suppose that a time series 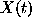 is a stationary stochastic
process with zero mean defined by a set of realizations
is a stationary stochastic
process with zero mean defined by a set of realizations
To describe gaps in observations we introduce the time window function
With this notation the observed time series can be represented as
Calculate the periodogram:
where <> denotes averaging over the set of realizations.
Under the conditions stated above, the relationship between the
periodogram 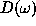 and the power spectrum
and the power spectrum 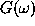 is given by
the convolution
is given by
the convolution
where the spectral window function 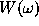 is the periodogram of the
time window function
is the periodogram of the
time window function
Now, from Eq. (43), for the correlogram 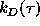 and the correlation window
and the correlation window 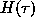 , introduced as
inverse Fourier transforms of
, introduced as
inverse Fourier transforms of 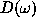 and
and 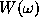 respectively,
one has:
respectively,
one has:
where 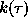 is the auto-correlation function of
is the auto-correlation function of 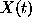 .
For further details the reader is referred to
Jenkins & Watts (1968), Deeming (1975), Otnes &
Enocson (1978), Marple (1978), and Terebish (1992).
.
For further details the reader is referred to
Jenkins & Watts (1968), Deeming (1975), Otnes &
Enocson (1978), Marple (1978), and Terebish (1992).
In interferometry (Esepkina et al. 1973; Thompson et al. 1986),
the intensity of radiation from any source on the sky can be
described in terms of position 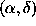 , wavelength
, wavelength 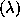 ,
and time (t).
Each measurement is an average over a band of wavelengths and over
some span of time. Here, the one-dimensional, monochromatic, and
instantaneous approximation is used to simplify the discussion.
The resulting specific intensity
,
and time (t).
Each measurement is an average over a band of wavelengths and over
some span of time. Here, the one-dimensional, monochromatic, and
instantaneous approximation is used to simplify the discussion.
The resulting specific intensity 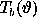 that describes the
distribution of the source brightness along the arc of a circle
that describes the
distribution of the source brightness along the arc of a circle
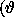 is the angular coordinate) has a Fourier transform
is the angular coordinate) has a Fourier transform
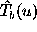 ,
which is called the spectrum of spatial frequencies. Correspondingly,
when an interferometer measures the visibility data
,
which is called the spectrum of spatial frequencies. Correspondingly,
when an interferometer measures the visibility data 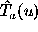 ,
the image, or the map,
,
the image, or the map, 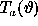 can be calculated by the Fourier
transform of
can be calculated by the Fourier
transform of 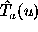 . Two fundamental relations are valid:
. Two fundamental relations are valid:
where 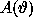 is the beam of interferometer and
is the beam of interferometer and
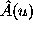 is
the transfer function. Eq. (47) determines an interferometer as
a filter of spatial frequencies, whereas Eq. (46) explains why,
due to convolution of
is
the transfer function. Eq. (47) determines an interferometer as
a filter of spatial frequencies, whereas Eq. (46) explains why,
due to convolution of 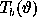 with the beam
with the beam 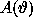 ,
the resulting
image is called a dirty map.
,
the resulting
image is called a dirty map.
Upon close examination one can see that in both sciences the rigorous (theoretical) quantities are introduced at the first level. In the spectral-analysis case they are the power spectrum and the correlation function; in the interferometry their counterparts are the distribution of brightness and the spatial spectrum. At the second level we have estimators of the strict quantities. In spectral analysis, they are the periodogram and the correlogram, whereas in the interferometry these are the map and the visibility data, respectively. Finally, equations which connect the quantities of the two levels are identical (convolution and multiplication ) and include the characteristics of observations: the beam and the transfer function and their analogs, i.e., the spectral window and the correlation window.
In reality, due to the finite dimensions of mirrors and the finite
time spans of observations we cannot get the true quantities,
and all we can do is to find their optimal
approximations.
In optics or in radio astronomy, when filled
apertures are used, the maps are produced directly in the focal
plane
of a telescope. Analogously, when the time series is given
at all points of some interval or at time points regularly spaced
within the interval, the evaluation of the periodogram can be made
quite easily. When an interferometer is used, the aperture is not
solid, and what we can measure is the visibility data, i.e., the
estimator of the spectrum of spatial frequencies. The longer the
baseline, the smaller the area of the 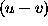 -plane (u-domain in the one-dimensional
case) filled, and the more dirty the resulting map becomes.
-plane (u-domain in the one-dimensional
case) filled, and the more dirty the resulting map becomes.
To overcome this, various techniques of aperture synthesis are
used, and this leads to complete solution of the problem since
the 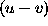 -plane is completely filled. If the aperture
synthesis provides partial filling of the
-plane is completely filled. If the aperture
synthesis provides partial filling of the 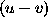 -plane, the
cleaning procedures can be used with the aim of eliminating
the artifacts of the ``holes'' in the
-plane, the
cleaning procedures can be used with the aim of eliminating
the artifacts of the ``holes'' in the 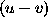 -plane from the map. We have the
same problems in the spectral-analysis case, when the
time points are distributed irregularly or have long gaps. In
this case the correlograms cannot be determined for all values of
time lag
-plane from the map. We have the
same problems in the spectral-analysis case, when the
time points are distributed irregularly or have long gaps. In
this case the correlograms cannot be determined for all values of
time lag  , and this would give false features in the resulting
periodograms. The main aim of the present
paper is to answer the question: is it possible to apply the
aperture synthesis method to spectral analysis of time series?
, and this would give false features in the resulting
periodograms. The main aim of the present
paper is to answer the question: is it possible to apply the
aperture synthesis method to spectral analysis of time series?
It is known that to do
aperture synthesis one must have an interferometer with the
changeable baseline. Of all the schemes of the aperture synthesis
the one proposed by Ryle (1960) is the most suitable for us.
This consists of two antennas A and B fixed at
separation L. The third antenna C is moving inside the
interval 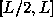 . At each position of the moving antenna one
obtains two interferometers (CB) and (AC) with the baselines l
and
. At each position of the moving antenna one
obtains two interferometers (CB) and (AC) with the baselines l
and 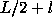 , and they yield the values of the visibility data
, and they yield the values of the visibility data 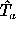 at the points
at the points 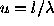 and
and 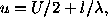 where
where 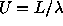 .
Obviously,
while antenna C sweeps all the interval
.
Obviously,
while antenna C sweeps all the interval 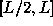 , the visibility
data
, the visibility
data 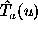 become available at all points of the interval
become available at all points of the interval 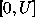 .
.
Now we apply this idea to time series analysis.
Every two points spaced at
the distance  may be called the Time Interferometer
with variable
baseline
may be called the Time Interferometer
with variable
baseline  , since each such pair yields the estimation
of the correlation function
, since each such pair yields the estimation
of the correlation function 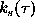 by averaging the
products
by averaging the
products 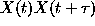 over the set of realizations. The value
over the set of realizations. The value
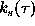 can be obtained no matter where the
points t and
can be obtained no matter where the
points t and 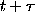 are located inside the interval
are located inside the interval 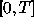 .
This follows
from our assumption that
.
This follows
from our assumption that 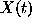 is a stationary stochastic process,
and that is crucial for our study.
is a stationary stochastic process,
and that is crucial for our study.
Assume that the time series is given at two points 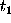 and
and 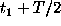 . This Time Interferometer allows
us to get the correlation function only at the point
. This Time Interferometer allows
us to get the correlation function only at the point 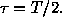 Let
us make new observations at the points
Let
us make new observations at the points 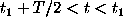 +
T. It is clear that each new point
+
T. It is clear that each new point 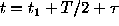 yields two
additional values of the correlation function, namely, at the points
yields two
additional values of the correlation function, namely, at the points
 and
and 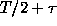 . Obviously, when the observations cover the
interval
. Obviously, when the observations cover the
interval 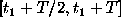 , the values of
, the values of
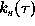 become available at
all points of the interval
become available at
all points of the interval 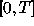 .
.
Now we see that the
fixed antennas A and B in the Ryle interferometer
are the counterparts of the boundary
points 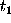 and
and 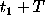 , while each new position of the moving
antenna C is nothing else but the new point of observations.
Since Ryle's interferometer makes the synthesis of the visibility
data, it is a good reason to call the described procedure
the synthesis of the correlation function.
, while each new position of the moving
antenna C is nothing else but the new point of observations.
Since Ryle's interferometer makes the synthesis of the visibility
data, it is a good reason to call the described procedure
the synthesis of the correlation function.
Obviously, complete synthesis and the evaluation of 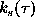 from
an even time series are the same. Thus, with
from
an even time series are the same. Thus, with 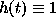 elsewhere
for the synthesized periodogram we get
elsewhere
for the synthesized periodogram we get
This estimator yields the clean spectrum, i.e., free of the false peaks
that come from the ``holes'' in the  -domain.
-domain.
To proceed further,
assume that we have a gap in the observations. Let the length of the
gap be l and the longest distance between the borders of the
gap and the boundary points of the interval 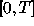 be a. If
be a. If 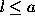 then the correlation function can be evaluated at all
points
then the correlation function can be evaluated at all
points 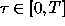 , otherwise only on the subintervals
, otherwise only on the subintervals 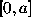 and
and
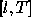 . In this case the correlation function
turns out to be synthesized at all points except the
``hole'' of the length l-a, and, consequently, the synthesized
periodogram
. In this case the correlation function
turns out to be synthesized at all points except the
``hole'' of the length l-a, and, consequently, the synthesized
periodogram 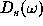 calculated from Eq. (48)
will not be clean.
Nevertheless, it is less contaminated than the periodogram calculated
directly from Eqs. (42). Thus we see that to clean the spectrum
completely, one needs to perform more observations until the condition
calculated from Eq. (48)
will not be clean.
Nevertheless, it is less contaminated than the periodogram calculated
directly from Eqs. (42). Thus we see that to clean the spectrum
completely, one needs to perform more observations until the condition
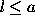 becomes true.
becomes true.
When the only realization is available, averaging over the ensemble should be replaced with averaging over time. For further development of the method the reader is referred to Vityazev (1996).
Deeming, T. J. 1975, Ap&SS, 36, 137
Esepkina, N. A., Korolkov, D. N., & Pariysky, Yu. N. 1973, Radio telescopes and Radiometers (Moscow: Nauka)
Jenkins, G. M., & Watts, D. G. 1968, Spectral Analysis and its Applications (San Francisco: Holden-Day)
Marple, Jr., S. L. 1987, Digital Spectral Analysis with Applications (Englewood Cliffs, NJ: Prentice-Hall)
Otnes, R. K., & Enocson, L. 1978, Applied Time Series Analysis (New York: Wiley-Interscience)
Ryle, M., & Hewish, A. 1960, MNRAS, 120, 220
Terebish, V. Yu. 1992, Time Series Analysis in Astrophysics (Moscow: Nauka)
Thompson, A. R., Moran, J. M., & Swenson, G. W. Jr. 1986, Interferometry and Synthesis in Radio Astronomy (New York: Wiley)
Vityazev, V. V. 1996, Astron. and Astrophys. Tr., in press
Next: A New Stable Method for Long-Time Integration in an N-Body Problem
Previous: Time Series Analysis of Unequally Spaced Data: Intercomparison Between Estimators of the Power Spectrum
Up: Algorithms
Table of Contents - Index - PS reprint - PDF reprint