Next: Calibration and Performance Control for the VLT Instrumentation
Previous: WinTICS-24 Version 2.0 and PFITS-An Integrated Telescope/CCD Control Interface
Up: Instrument-Specific Software
Table of Contents - Index - PS reprint - PDF reprint
Astronomical Data Analysis Software and Systems VI
ASP Conference Series, Vol. 125, 1997
Editors: Gareth Hunt and H. E. Payne
M. R. Rosa1
Space Telescope European Coordinating Facility, European Southern Observatory, D-85748 Garching, Germany,
E-mail: mrosa@eso.org
1Affiliated to the Astrophysics Division of the Space Science Department,of the European Space Agency
Abstract:
This contribution revolves about computer models of astronomical instruments
and their application in advanced calibration strategies and observation
model based data analysis. The historical connection between calibration and
data analysis is reviewed. The success of physical models in the analysis
of observational data with strong instrumental signatures is shown, and a
concept for model based calibration developed. A discussion of advantages for
observatory operations, observing, pipeline processing, and data interpretation
is accompanied by a briefing about the current status of the
Observation Simulation and Instrument Modeling project at the ST-ECF and ESO.
The increasing importance assigned to tasks circumscribed by the terms
``calibration'' and ``data reduction'' reflects the evolution of equipment
and the fact that purely morphological investigations have largely been
superseded by the demand to turn the last bit of useful information in
raw data into significant astrophysical quantities.
Calibration strategies currently adopted are empirical methods aimed
at ``cleaning'' raw data of instrumental and atmospheric
effects. Since it is only through the empirical determination of
calibration reference data (e.g., dispersion relations, flat fields,
sensitivity curves) that both evils-changes of the instrument and
changes of atmospheric conditions, respectively-are detected and their
effects removed, these calibration strategies often take on the form
of a defensive battle repeatedly fought every night.
Space based instrumentation, in particular IUE and HST, has taught
that once the effect of the human desire to tweak the instrumental
parameters every so often is nullified, pipeline calibration of the
raw data can efficiently be implemented. Monitoring and trend analysis of
the calibration parameters also shows that predictions made about the
instrumental characteristics are usually very reliable. Operational scenarios
with pipeline calibration are now also being planned for ground based
observatories (e.g., ESO's VLT), and it is easy to show that once instrument
stability through configuration control is achieved, all that remains of
nightly calibration data taking is to address environmental aspects,
e.g., the atmospheric transmission.
Nevertheless, the calibration process remains of the
``instrument signature removal'' type, even if based on predicted,
less noisy calibration data. A long learning process is required to
determine the optimum deployment of resources-manpower and
observing time-for the calibration task as a whole, and for its
subprocesses. This approach also hides the direct link between the engineering
parameters of instruments and the differing characteristics in closely
related configurations (e.g., the 2-D pattern of echellograms obtained
with different grating tilts).
Repeatedly, situations arise where the scrutinizing analysis of science data,
in particular when combined with very specific theoretical
expectations (e.g., stellar atmospheric models, evolutionary color diagrams),
reveals shortcomings or omissions in the ``signature removal''
calibration. Usually the effects found are neither new to the type of
instrument (e.g., non-linearity of a detector) nor unexpected on physical
grounds (e.g., scattered light in grating spectrographs). To be fair, almost
always the embarrassing situation is not a result of an oversight but rather
a consequence of the calibration strategy employed-dealing
piecemeal with a highly complex interrelation of physical effects.
Can we do any better? In the following I will lay out the arguments for
a radically new approach, highlighting a few examples, and briefly report
on the activities in an collaborative ESO/ST-ECF effort to implement
observational data calibration and analysis on the basis of physical
models.
Usually the calibration and data analysis process is conceived as a
well defined activity, detached from, but linking the observational
process with the astrophysical interpretation. The direction is from
raw data to better (i.e., ``cleaned'') data, from counts per pixel to
H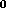 . What really happened during the observation was, however, the
application of an operator O onto a vector u representing
a subvolume of the many-D universe. O describes the equipment
used as well as any other environmental circumstances (e.g., the
atmosphere).
. What really happened during the observation was, however, the
application of an operator O onto a vector u representing
a subvolume of the many-D universe. O describes the equipment
used as well as any other environmental circumstances (e.g., the
atmosphere).
Were it not for the ultimate limitation imposed by noise, we
could try to just find and apply the inverse operator C to
calibrate, i.e., recover u from the raw data d, and then
go on to interpret u. Eventually the more rewarding ``data analysis''
strategy is to subject a range of probable u to a model of the
data taking process O
to a model of the
data taking process O and to compare the resultant simulated
data d
and to compare the resultant simulated
data d with the actual d.
with the actual d.
Practically, finding C empirically is hampered not only by noise,
but also by
the fact that O is huge, while we can spend only so much time
exploring the parameter space-science exposures are certainly more
rewarding. It would help if we had a good idea of what O looks like.
All that is necessary, on paper, is a complete description of the important
physical aspects of the instruments. We will see below how far one can go
in reality.
In essence, one can implement a two stage process to achieve substantial
improvements over the canonical ``signature removal'' data analysis.
Step 1 consists of casting physical principles into code which is capable
of simulating observational data. This can be used to generate calibration
references that are noise free and contain controllable engineering parameters.
At this stage it is straightforward to generate calibration data for a
large array of modes that would otherwise have to be covered painstakingly
by individual calibration exposures. After having gained confidence in
stage 1, application of optimization techniques, e.g., simulated
annealing to simulated data using the physical instrument model, will
be step 2 (cf. Rosa 1995).
It is important to note that the process described above differs
substantially from many seemingly similar schemes, in that the kernel
is an instrument model based on first principles. In observation
planning, it is now common practice to simulate the outcome of proposed
observations by convolving target models with empirical spectral
response curves, adding noise and whatever else the calibration data
base can provide. Good examples are the WWW planning tools for the HST
instruments. It has also become standard technique now, thanks again
to HST, to apply deconvolution techniques and derivatives such as
multiple frame analysis (see Hook 1997) to data sets-techniques
that usually work best if fed by sophisticated models of
the PSF (e.g., TinyTim of HST). Calibration data for HST instrument
modes that can not be obtained for reasons of limited time are usually
supplied by interpolation between neighboring modes and for
all modes forecasted by trend analysis.
The complete physical model of an instrument, in principle, incorporates
many of those capabilities. In fact its construction and
tuning to actual performance requires a deep understanding based
on the experiences gained with many of the tools described above. The big
difference is its predictive power.
Exercises such as the FOS scattered light correction (Rosa 1994;
Bushouse, Rosa, & Müller 1995) or the FOS dispersion model (Dahlem &
Rosa 1997,in preparation) demonstrate that a software model, covering just one
particular aspect (here the diffraction and interference properties of
gratings and apertures, and the reimaging electron optics of
digicons), but going beyond a simple throughput calculation,
i.e., correctly describing all relevant physical effects, can be very
beneficial in solving problems encountered during the scientific
analysis of data. Used in this way, the model appears simply as an
additional data analysis tool in support of the calibration process.
However, the purpose of this paper is to go one step further, i.e., to
advance beyond the ``signature removal'' calibration strategy currently
in use. Had the FOS model been available early on, it would certainly
have influenced the specifications for the pipeline, and even earlier
the introduction of solar blind detectors.
Obviously, it is necessary to correctly describe all aspects of an
instrument to such a degree that the typical percent level accuracy of
the canonical calibration can be surpassed. The FOS models mentioned
above do not need to incorporate geometric and intensity aspects at
once. On the other hand, a model designed to completely cope with the
analysis of long slit echelle spectra must be able to predict the
geometrical pattern (curvature of orders, of slit images and field
distortions), and the blazed sensitivity variations in dispersion
direction as well as the spatial intensity profiles (LSF and
interorder background).
A generic echelle spectrograph model, such as described above, is currently
under construction in a collaborative effort between ESO and the ST-ECF.
Its immediate application will be to the UVES spectrograph under construction
for the VLT observatory and the STIS instrument to be working on HST after
the servicing mission in February 1997.
The basis of this effort is a library of C++ classes that provide
equipment modules, e.g., grating, mirror, filter, detector, and
optical rays (the targets passing through the equipment), as well as
modules for other ingredients such as targets, interstellar extinction,
and atmospheric properties to compose instrument models and simulate
observations (see also Ballester, Banse, & Grosbøl 1997).
References:
Ballester, P., Banse, K., & Grosbøl, P. 1997, this volume
Bushouse, H. E., Rosa, M. R., & Müller, Th. 1995, in Astronomical Data Analysis Software and Systems IV, ASP Conf. Ser., Vol. 77, eds. R. A. Shaw, H. E. Payne & J. J. E. Hayes (San Francisco, ASP), 345
Hook, R. N. 1997, this volume
Rosa, M. R. 1994, in Calibrating Hubble Space Telescope, eds.
C. Blades & S. Osmer (Baltimore: STScI), 190
Rosa, M. R. 1995, in Calibrating and Understanding HST and VLT
instruments, ed. P. Benvenuti, ESO/ST-ECF Workshop, ESO, 43
© Copyright 1997
Astronomical Society of the Pacific,
390 Ashton Avenue, San Francisco, California 94112, USA
Next: Calibration and Performance Control for the VLT Instrumentation
Previous: WinTICS-24 Version 2.0 and PFITS-An Integrated Telescope/CCD Control Interface
Up: Instrument-Specific Software
Table of Contents - Index - PS reprint - PDF reprint
payne@stsci.edu
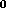 . What really happened during the observation was, however, the
application of an operator O onto a vector u representing
a subvolume of the many-D universe. O describes the equipment
used as well as any other environmental circumstances (e.g., the
atmosphere).
. What really happened during the observation was, however, the
application of an operator O onto a vector u representing
a subvolume of the many-D universe. O describes the equipment
used as well as any other environmental circumstances (e.g., the
atmosphere).
 to a model of the
data taking process O
to a model of the
data taking process O and to compare the resultant simulated
data d
and to compare the resultant simulated
data d with the actual d.
with the actual d.