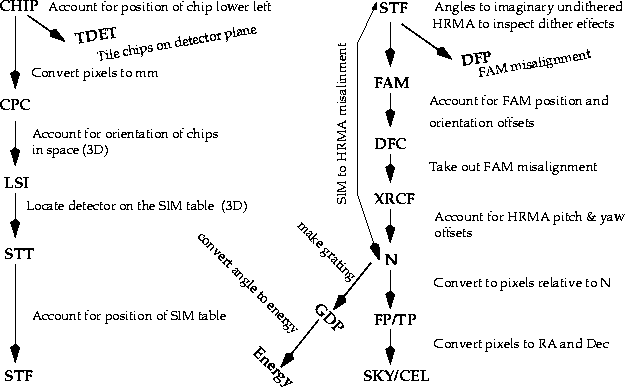
Figure: ASC coordinate systems and the transformations. Original PostScript figure (10kB).
Next: Simulated AXAF Observations with MARX
Previous: Implementation Design of the ASC Data Model
Up: AXAF
Table of Contents - Index - PS reprint - PDF reprint
H. He, J. McDowell, M. Conroy
Smithsonian Astrophysical Observatory, 60 Garden Street,
Cambridge, MA 02138, E-mail: hhe@cfa.harvard.edu
Pixlib library is intended to perform AXAF Science Center (ASC) coordinate system data analysis. The library facilitates space telescope simulations dealing with five science instruments (SI) or detectors (e.g., ACIS, HRC-I), each constructed up to ten chips. The pixlib is designed to be a structured system, to promote system extensibility and maintainability. The fundamentals of the program are provided by a number of modules which rely on external parameter interface files. The parameter files determine the essential characteristics of the ASC coordinate systems. The coordinate transformation computation utilizes matrix arithmetic algorithms for coding efficiency and software reusability. The integrated library provides a comprehensive collection of functions for user applications, and these functions are well documented, easy to use, and FORTRAN-binding compatible. At the present, the library affords more than 50 transformations among ~20 ASC coordinate systems.

Figure: ASC coordinate systems and the transformations.
Original PostScript figure (10kB).
Figure 1 lists the most important ASC coordinate systems and sketches the transformation paths among them. Items threaded by line arrows denote coordinate systems, e.g., CHIP for 2-D chip pixel coordinates, CPC 2-D chip physical coordinates in mm, TDET 2-D tiled detector plane pixel coordinates, and LSI for local SI coordinates. The line arrows connecting a pair of coordinate systems indicate the coordinate transformation is both forward and backward, and the aim of the transformation is explained at the side. For instance, transformation of CPC to LSI is to account for chip orientation in space, and N to FP is to convert the 3-D HRMA nodal position to the 2-D pixel focal plane coordinates. Details on the definitions and determinations of the ASC coordinate systems are discussed in a memo (McDowell 1996).
The goal of pixlib is to build up a software framework
for the coordinate systems outlined above, and provide functions to
perform the coordinate transformations between any two systems.
Borrowing from the C++ class concept,
the pixlib distinguishes ``private'' (lower-level) data/functions
and ``public'' (upper-level) routines. The private section, composed of
more than five independent modules, is constructed on a set of external
parameter files that hold the definitions and aspects of the ASC
coordinate systems (to be discussed in next section).
A struct member is defined in each module in order to
handle the interface with the external files. The initiated data members
of the struct are then passed to the function members of the module
that are to be invoked in the upper-level applications.
Several important
modules of the telescope simulator are briefed below.
The function of module pix_detplan.c is to
layout chips on a TDET plane following the specifications
(e.g., chip lower-left
corner position and orientation, etc.) given in relevant parameter files.
The motivation for introducing TDET is that
the AXAF detector chips do not lie in a plane, making it difficult to inspect
simultaneously both individual chip pixels and an overall
geometry of the detector. To retain this information, chips are tiled in an
approximately correct relative orientation, but the chip edges
are paralleled and the gaps between the chips are edged.
The pix_grating.c subsystem focuses on grating observation
of a dispersed spectrum, determining the
photon energy given a zero-order position for the undispersed photon
trajectory, or traces the dispersed photon trajectory for a given energy.
Module pix_chip2stf.c sets up CHIP, CPC,
LSI, STT, and STF coordinate systems, and provides
methods for the system transformations.
Similarly, pix_stf2tpc.c and pix_tpc2src.c initiate
the rest of coordinate systems and complete the
transformations between STF and CEL.
By providing a rich collection of transformation functions, the ``public'' module hides the details of the implementations by wrapping one or more lower-level method(s). Unlike the lower-level programs, which are especially heavy on pointer manipulation, the upper-level functions are controlled by arguments passed by value. This type of manipulation was particularly desirable, since it allows FORTRAN-binding compatibility. Once the coordinate framework is built (or initiated), a requested transformation call from, say, CPC to FP, is able to output coordinates in CPC for given coordinates in FP without asking for other inputs.
The pixlib adopts SAO IRAF-compatible parameter file(s) as data I/O structure. There are six parameter files which are generalized from experimental or calibration data (McDowell 1996). These files specify several primary coordinate origins, relevant orientations, and others. Those are described as follows.
pix_origin_table.par sets eleven AXAF primary coordinate
system origins in spacecraft and HRMA nodal coordinates,
pix_tdet_planesys.par defines
nine TDET plane systems (dimension and center) of the five detectors,
pix_tdet_nomfocus.par determines
nominal focus points of TDET plane systems,
pix_tdet_refcoords.par specifies
the lower-left corner positions in TDET of 17 chips,
pix_corner_lsi.par maps 2-D chip corner
positions to 3-D LSI coordinates,
pix_sim_table.par defines seven aim-points, the offsets from
SIM transformation table ( STT), of detectors, and
pix_size_cntr.par constitutes 2-D instrumental pixel systems
(i.e., SKY, FP, TP, and GDP) and grating properties.
The data are entered in the parameter files as a string, such as ``(x, y, z)'', in order to retain clarity. The string is interpreted back into the individual numbers when the file is opened. These coordinate system definition files are hidden from the user and looked up internally, once per run, in lower-level modules during the pixlib initiation. On the other hand, an additional parameter file is created specially for user interface. It allows the user to specify the chip of a detector, aim-point, focal plane system, etc. for performing a telescope simulation or data analysis.
The pixlib coordinate transformation computations are performed with matrix arithmetic. A portable matrix library package provides utilities to handle matrix algebra (i.e., vector-vector cross/dot/addition/subtraction, matrix(vector)-matrix multiple, matrix transpose/compose). Specifically, we use homogeneous coordinates (Salmon & Slater 1987) to simplify further matrix representation of coordinate transformations. Application of homogeneous coordinates to the ASC coordinate systems is briefly described below.
Coordinate transformation from frame A to frame B can be concisely
expressed as 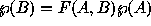 .
Where
.
Where 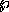 is a
is a 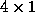 homogeneous coordinate vector, defined as
homogeneous coordinate vector, defined as
 for
a conventional 3-D spatial vector
for
a conventional 3-D spatial vector 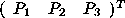 .
.
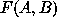 is a
is a 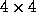 transformation matrix expressed in terms of
rotation and translation matrices,
transformation matrix expressed in terms of
rotation and translation matrices,
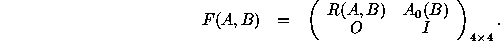
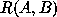 above denotes a
above denotes a 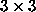 A-to-B rotation matrix,
A-to-B rotation matrix,
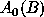 a
a 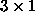 translation (column) matrix of frame A origin
in frame B.
translation (column) matrix of frame A origin
in frame B.
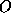 is
is 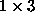 zero matrix and I
zero matrix and I 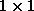 unit matrix.
To obtain the backward B-to-A transfer,
unit matrix.
To obtain the backward B-to-A transfer,
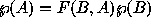 ,
the corresponding rotation and translation matrices for
the
,
the corresponding rotation and translation matrices for
the 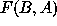 are derived, assuming
are derived, assuming 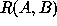 orthogonal, as
orthogonal, as
We use a transformation struct to compose the matrices, or
arrays of 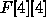 ,
, 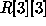 , and
, and 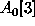 , for reusability.
The struct is dynamically
allocated and instantiated when a upper-level request is called. The values of
, for reusability.
The struct is dynamically
allocated and instantiated when a upper-level request is called. The values of
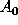 and R elements are either taken from the parameter files or
derived by parsing arguments, and
the F are then composed with the known
and R elements are either taken from the parameter files or
derived by parsing arguments, and
the F are then composed with the known 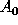 and R.
The requested coordinate
transformation from A to B is thus completed by a matrix-vector multiple
performance.
and R.
The requested coordinate
transformation from A to B is thus completed by a matrix-vector multiple
performance.
We are grateful to SAO colleagues for offering discussions and knowledge regarding the paper. This project is supported from the AXAF Science Center (NAS8-39073).
McDowell, J. 1996, ASC Coordinates, Revision 4.0, SAO/ASCDS
Salmon, R., & Slater, M., 1987, Computer Graphics: Systems and Concepts (Reading, MA: Addison-Wesley)
Next: Simulated AXAF Observations with MARX
Previous: Implementation Design of the ASC Data Model
Up: AXAF
Table of Contents - Index - PS reprint - PDF reprint