 universe.
universe.
Next: On Fractal Modeling in Astrophysics: The Effect of Lacunarity on the Convergence of Algorithms for Scaling Exponents.
Previous: Refined Simplex Method for Data Fitting
Up: Modeling
Table of Contents - Index - PS reprint - PDF reprint
G. J. Ferland, K. T. Korista, and D. A. Verner
Physics & Astronomy, University of Kentucky, Lexington, KY 40506
A complete simulation involves many hundreds of stages of ionization,
many thousands of levels,
with populations determined by a vast sea of atomic/molecular processes,
many with accurate cross
sections and rate coefficients only now becoming available. The scope of
the calculations and the
numerical techniques they use, can be improved as computers grow ever faster,
since previous
calculations were naturally limited by the available hardware.
The final part is the application to observations, driven in part by the
revolution in quality of spectra
made possible by advances in instrumentation. The galactic nebulae
represent laboratories for checking
whether the physics of nebulae is complete and for testing galactic chemical
evolution theories, and can
validate the analysis methods to be used on the quasars. Models of
ablating molecular clouds, the
likely origin of some gas in quasars, are tested by studies of the Orion
complex. Finally, the quasars
themselves present the ultimate challenge: to deduce the composition of
their emitting gas from the
spectrum, determine the dependencies of this spectrum on the shape of the
ionizing continuum,
correlating this with observed changes in the spectral energy distribution,
and finally to understand its
dependencies on luminosity (the Baldwin effect). Once the emission line
regions of quasars are
understood, we will have a direct probe of the  universe.
universe.
Cloudy is widely used in the astronomical community, with roughly 50 papers per year employing it. The code is a general spectroscopic tool whose development has an impact well beyond out specific studies.
The quasars are the most luminous objects in the universe and the
highest redshift objects we can observe directly. Understanding their
emission lines has a cosmological imperative, since their spectra depend
on luminosity (Baldwin 1977; Boroson & Green 1992; Osmer et al. 1994).
Once we can directly measure their luminosity, the quasars will gauge the
expansion of the universe at redshifts  . At the same time,
the origin of the chemical elements remains a central theme across much
of stellar, galactic, and extragalactic astrophysics. Quasars probe
early epochs in the formation of massive galaxies and their emission
lines can reveal the composition of the interstellar medium (ISM) when
the universe had an age well under a billion years. Within our galaxy, HII
regions and planetary nebulae define the end points of stellar evolution.
Detailed analysis of their emission line spectra can reveal both the
nebula's composition and the luminosity and temperature of the central
star(s), and can validate the analysis methods to be used for the quasars.
. At the same time,
the origin of the chemical elements remains a central theme across much
of stellar, galactic, and extragalactic astrophysics. Quasars probe
early epochs in the formation of massive galaxies and their emission
lines can reveal the composition of the interstellar medium (ISM) when
the universe had an age well under a billion years. Within our galaxy, HII
regions and planetary nebulae define the end points of stellar evolution.
Detailed analysis of their emission line spectra can reveal both the
nebula's composition and the luminosity and temperature of the central
star(s), and can validate the analysis methods to be used for the quasars.
Deducing reliable abundances and luminosities of galactic and extragalactic
emission line objects is
the central theme of the development of Cloudy. Emission lines are produced
by warm (~104K) gas
with moderate to low density (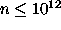 cm-3).
Such gas is far from equilibrium, and its physical
conditions cannot be known from analytical theory.
Rather, the observed spectrum is the result of a
host of microphysical processes which must be simulated numerically.
cm-3).
Such gas is far from equilibrium, and its physical
conditions cannot be known from analytical theory.
Rather, the observed spectrum is the result of a
host of microphysical processes which must be simulated numerically.
The ionization, level populations, and electron temperature are determined self-consistently by solving the equations of statistical and thermal equilibrium. Lines and continua are optically thick and their transport must be treated in detail. Predictions of the intensities of thousands of lines and the column densities of all constituents result from the specification of only the incident continuum, gas density, and its composition. By their nature, such calculations involve enormous quantities of atomic/molecular data describing a host of microphysical processes, and the codes involved are at the forefront of modern computational astrophysics. Although the task is difficult, the rewards are great, since numerical simulations make it possible to interpret the spectrum of non-equilibrium gas on a physical basis. Cloudy has been developed as an aid to this interpretation, much as an observer might build a spectrometer.
The next few years will witness first light of a large number of new optical to infrared observational facilities, and we will be in a position to obtain spectra of faint objects with unprecedented precision. The basic atomic data base is growing in both precision and size, and high-end workstations have the power of yesterday's supercomputers-large scale numerical simulations and spectral synthesis can now be done with unprecedented precision and facility. Cloudy is openly available, and other astronomers use it to publish roughly 50 refereed papers per year. It is a general spectroscopic tool whose development has an impact well beyond the specific studies undertaken here.
Cloudy's source (about 110,000 lines of FORTRAN) and its documentation Hazy, a Brief Introduction to Cloudy (UK Physics Internal Report, 461 pages), are freely available on the Cloudy home page. This Web page also has group preprints, and Dima Verner's Atomic Data for Astrophysics (ADfA) Web page provides public access to the numerical forms of the atomic data used by Cloudy.
A major use of spectral synthesis calculations is to deduce the conditions and abundances in the matter producing a spectrum. There is always a question of uniqueness since there may be more than one way to get any particular result, and we must work backwards to deduce the question (properties of the object) from the answer (the spectrum). Examining predictions over the very broadest possible range of physical parameters is vital to really understand what a spectrum is telling us. Today we usually use the code to generate very large grids, involving thousands of complete simulations, to generate contour or 3-D plots like that shown in Figure 1.
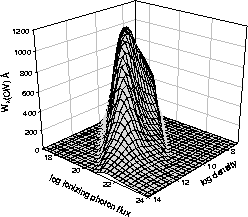
Figure: CIV 1549 equivalent width for a wide
range of densities and flux of photons.
Original PostScript figure (488kB).
This is an example, based on Baldwin et al. (1995), showing that one of the strongest quasar emission lines is most efficiently produced over a very narrow range of conditions. The peak visibility occurs for the parameters long ago deduced as ``standard'' quasar conditions. We argued that this is just a selection effect.
A major effort has gone into making it possible to generate such large grids on a routine basis. Issues include the following:
The code must have enough intelligence to autonomously converge for models with very different conditions, without user intervention. This goal has largely been realized. All of the predictions shown here are the result of fully autonomous calculations with no outside intervention.
The code must respond appropriately, no matter what conditions it is
asked to compute. It goes to
the Compton, molecular, ISM, and LTE limits. The temperature limits are
2.8K<T<109K, and
density limit 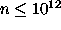 cm-3
because of the approximate treatment of line transfer, and since most ions
are treated as two-level systems. The code will identify conditions which
are inappropriate for its use.
cm-3
because of the approximate treatment of line transfer, and since most ions
are treated as two-level systems. The code will identify conditions which
are inappropriate for its use.
The code must examine its results and predictions to confirm that the simulation is valid. It simply is not possible to go over the many tens of megabytes of results generated in large grids, after the fact, to confirm that all went well. As the code is developed, potential problems are identified and logic written to check for this in future calculations.
The code will probably converge a simulation with no problems, and it will certainly identify any problems at the end of the calculation. These are essential core features-vital if very large grids are to be computed reliably. Each simulation ends with a summary of all remarkable or surprising features, an analysis of any convergence problems, and checks that the range of validity was not exceeded. One specific example of these internal checks is that the code now tracks timescales for all heating-cooling and ionization-recombination reactions. At the end of the calculation the code will identify the longest timescale. A warning is produced if the time-steady assumption is not valid.
The code includes ~104 resonance lines from the 495 possible stages of ionization of the lightest 30 elements-an extension that required several steps. The charge transfer data base was expanded to complete the needed reactions between hydrogen and the first 4 ions and fit all reactions with a common approximation (Kingdon & Ferland 1996). Radiative recombination rate coefficients were derived for recombination from all closed shells, where this process should dominate (Verner & Ferland 1996). Analytical fits to Opacity Project (OP) and other recent photoionization cross sections were produced (Verner et al. 1996). Finally, rescaled OP oscillator strengths were used to compile a complete set of data for 5971 resonance lines (Verner, Verner, & Ferland 1996).
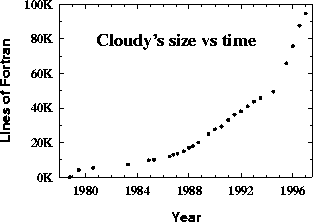
Figure: Cloudy's size as a function of time. This shows only the number
of executable lines of FORTRAN. The
total distributed source now constitutes
~110,000 lines of code.
Original PostScript figure (8kB).
Many other improvements are summarized in Ferland et al. (1997). Figure 2 shows a partial indicator of the scope of this activity, the number of lines of executable FORTRAN, as a function of time. The growth of the code in the past few years has been explosive, thanks to modern workstations.
This is the central difficulty in any large simulation since analytical answers are seldom known. Predictions are affected by the numerical approximations and atomic data used, as well as the presence of bugs which are certainly present in any large program. The best way to verify results is to compare completely independent calculations. We organized a workshop in 1994 to bring together researchers who have developed nebular codes. The result was the set of benchmarks published in the STScI Osterbrock-Seaton commemoration (Ferland et al. 1995). These benchmarks provide reference points to aid validation of any plasma code. We also make a continuous comparison of Cloudy with another independently written photoionization code, LineSpec (Verner & Yakovlev 1990).
Cloudy is widely used by others in their analysis and theory of spectroscopic observations. Figure 3 shows the number of refereed papers acknowledging the use of Cloudy through 1995.
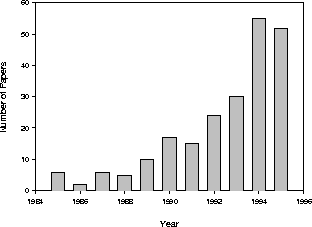
Figure: Refereed papers acknowledging Cloudy.
Original PostScript figure (5kB).
At least 138 papers were published in 1993-1995. Although I was not a co-author on these projects, the code did play some role in their execution.
The long-term goal is for the ionization and thermal equilibria of all species and the radiative transfer of continua and lines to be exact for all conditions. By this standard, the code is well over half-way complete.
A major effort has gone into Verner's Atomic Data for Astrophysics (ADfA) database. The results of any fully non-equilibrium calculation are no better than the underlying atomic data. New data appear throughout the physics and chemistry literature; maintaining the data base is a major ongoing effort, but one that does not directly result in publications. The ADfA contains basic atomic data required for calculation of the ionization state of astrophysical plasmas and for quantitative spectroscopy. The home page had more than 3000 visits and more than 4000 data files were retrieved during October 1995-October 1996. The contents of ADfA are driven by Cloudy's needs, which are defined by the spectroscopic problems. Because of this, and the public access we provide to our data, it has broad application to anyone working in quantitative spectroscopy.
We have placed a great deal of effort into deriving accurate fits to the best photoionization cross sections (Verner et al. 1996), the corresponding radiative recombination coefficients (Verner & Ferland 1996), and incorporating them into Cloudy. This effort is continuing, with the eventual goal of a complete photoionization cross section database, for all energies, of all atoms and ions of the first thirty elements. We plan the following developments:
We have calculated radiative recombination rates for all H-like, He-like, Li-like and Na-like ions of elements from H through Zn, and fitted them with convenient analytical formulae (Verner & Ferland 1996). Using our new fits to the excited shell photoionization cross section data described above, we shall complete the calculations of radiative recombination rates for ions of all isoelectronic sequences of all elements up to zinc (Z=30), and fit them by analytical formulae. This requires partial cross sections, and cannot be done with total cross sections, such as those available from the Opacity Project.
The majority of the ~104 heavy element lines now use collision strengths from g-approximations (Gaetz & Salpeter 1983; Mewe 1972). These can be computed on the fly for any line, but should only be used for transitions with no quantal calculations. The Iron Project (IP; Hummer et al. 1993) is producing large numbers of collision strengths which must be fitted and incorporated, if this remarkable data set is to be exploited. We will fit the IP data with a procedure drawing on our previous work on photoionization cross sections (Verner et al. 1996) and the asymptotic limits of Burgess & Tully (1992). We will develop a generalized scheme to represent the full temperature dependence in terms of analytical fits, with coefficients that can be stored along with other line information.
We have compiled accurate wavelengths, energy levels, and atomic transition probabilities for the permitted resonance lines of all ionization states of astrophysically important elements (Verner, Verner, & Ferland 1996), and these data are in Cloudy. Thus, the resonance line list is fairly complete. However, the set of forbidden and intercombination lines is not complete, especially for high ionization transitions of 3rd row and higher elements. Using our compilation of experimental energy levels, we will calculate accurate wavelengths for a complete list of forbidden and intercombination transitions between the lowest levels of all ions and elements included in Cloudy. We will compile atomic transition probabilities and collision strengths for them from literature and from available atomic databases, including the very recent database CHIANTI (Dere et al. 1996). All the collision strengths will be averaged over Maxwellian electron distribution, checked for asymptotic behavior by use of the Burgess & Tully (1992) method, and fitted over temperature with analytical formulae.
The ``Locally Optimally-emitting Clouds'' (LOC) model is outlined in Baldwin et al. (1995). The homogeneity of AGN spectra was long a mystery (Baldwin & Netzer 1978). Baldwin et al. (1995) showed that the average quasar spectrum can be produced by simply integrating over all possible clouds. Selection effects due to the line visibility function (Figure 1) ensure that most quasars will have very similar spectra even if their distributions of cloud properties are different.
The new aspect of this approach is allowing a range of cloud properties at a given radius, including ranges in column density and gas density. This seems much more realistic than just single-valued functions. Clouds of different gas densities could exist side-by-side for several viable confinement mechanisms (magnetically or shock confined, or dissipating clouds).
These integrations have been carried out over the full range of possible parameters. The line visibility functions are so strongly peaked that the spectrum of a typical quasar can be easily matched. This is not an entirely positive conclusion-we want to be able to deduce conditions in the quasar from the observations. The advantage is that there is no longer any hidden hand needed to adjust cloud parameters-we are dealing with a known, calculable, set of line visibility functions, which introduce powerful selection effects.
Two approaches are being taken. First we set up specific ``straw man'' distribution functions, compute the resulting spectrum, and compare this with observations. As an example, Broad Line Region (BLR) clouds could be radiatively driven outflows; we find that this can drive mass from main sequence stars near quasars. Such winds are Rayleigh-Taylor unstable, and they should cut off at an optical depth of unity in the Lyman continuum. We have carried out such an LOC integration, and find that the predicted lines can match observations. Radiatively driven winds are consistent with the observations.
The second approach is to use observations to try placing limits on possible distribution functions. We are working with Keith Horne (St. Andrews) to adopt our LOC grids, Keith's maximum entropy techniques (Horne 1994), and Jack Baldwin's line profile observations, to deduce the cloud distribution function. An integration over the full LOC plane produces results which are in good agreement with ``typical'' spectra of quasars (Baldwin et al. 1995). There is a large dispersion from object to object about this mean, which, together with detailed line profile studies, suggests that this plane is not necessarily fully populated in a given object. A goal is to determine observational limits to the cloud distribution functions. The combination of Keith's methods, Jack's observations, and our cloud simulations makes it possible to quantify which portions of the plane are populated, and whether this depends on luminosity.
For both approaches, we will first generate large data cubes containing predicted line equivalent widths as a function of gas density, column density, and flux at the illuminated face of the cloud. There will be a large number of these data cubes, with various continuum shapes and metallicities. Each will be incorporated into an interpolating routine, so that arbitrary parameters can be specified and the resulting spectrum obtained. Calculations of this core set of predictions is now underway and an initial atlas has been produced (Korista et al. 1997).
Our goal in these data cubes is to explore the implications of the LOC. However, this work has application well beyond our specific LOC models. Any other model of the BLR is only a subset of the LOC. Our grids will be made publicly available, so it will be possible for anyone to predict the spectrum resulting from a favored kinematic-spatial-magneto-hydrodynamic model, without becoming involved in the details of photoionization modeling.
The long-term
emphasis is to use luminous quasars to probe the high redshift universe.
The basic problem is to
understand luminosity correlations such as those in Baldwin, Wampler, &
Gaskell (1989), and Osmer
et al. (1994), on a physical basis. Luminosity-line correlations are
complicated by other correlations,
such as luminosity with continuum shape, most obviously
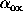 (Avni & Tananbaum 1986;
Worrall et al. 1987; however LaFranca et al. 1995 find no dependence,
and Avni, Worrall, &
Morgan 1995 find a complicated dependence). The NV/CIV relation discussed
by Hamann &
Ferland (1992, 1993) suggests a metallicity-luminosity correlation
(Ferland et al. 1996; Korista et al. 1997).
(Avni & Tananbaum 1986;
Worrall et al. 1987; however LaFranca et al. 1995 find no dependence,
and Avni, Worrall, &
Morgan 1995 find a complicated dependence). The NV/CIV relation discussed
by Hamann &
Ferland (1992, 1993) suggests a metallicity-luminosity correlation
(Ferland et al. 1996; Korista et al. 1997).
The LOC data cubes will be generated for many different continuum shapes,
which we characterize
by a Big Bump temperature,  , and slopes for the bump and
X-ray continuum. From this set, we can
search for line ratios more sensitive to the continuum shape than to the LOC
integration or metallicity.
The large data sets available from CTIO will be used, together with our
theoretical data sets, archival
X-ray and IR observations, to establish constraints
on the change in the
continuum shape. The CIV/Ly
, and slopes for the bump and
X-ray continuum. From this set, we can
search for line ratios more sensitive to the continuum shape than to the LOC
integration or metallicity.
The large data sets available from CTIO will be used, together with our
theoretical data sets, archival
X-ray and IR observations, to establish constraints
on the change in the
continuum shape. The CIV/Ly ratio is an example of lines that are
sensitive to changes in the ~30eV
continuum (Clavel & Santos-Lleo 1990). For the high redshift quasars, the
high energy end of the
Big Bump is a more important ingredient than the X-rays, and we can make
explicit predictions for
how line equivalent widths change with continuum shape. This work will
be extended using cloud
distribution functions, and the absence/presence of Baldwin effects in
various lines, to quantify
changes in the Big Bump with luminosity.
ratio is an example of lines that are
sensitive to changes in the ~30eV
continuum (Clavel & Santos-Lleo 1990). For the high redshift quasars, the
high energy end of the
Big Bump is a more important ingredient than the X-rays, and we can make
explicit predictions for
how line equivalent widths change with continuum shape. This work will
be extended using cloud
distribution functions, and the absence/presence of Baldwin effects in
various lines, to quantify
changes in the Big Bump with luminosity.
The development of Cloudy would not have been possible without the continued support of NASA and the NSF.
Avni, Y., & Tananbaum, H. 1986, ApJ, 305, 83
Avni, Y., Worrall, D. M., & Morgan, W. A. 1995, ApJ, 454, 673
Baldwin, J. A. 1977, MNRAS, 178, 67p
Baldwin, J., Ferland, G., Korista, K., & Verner, D. 1995, ApJL, 455, L119
Baldwin, J. A., & Netzer, H. 1978, ApJ, 226, 1
Baldwin, J., Wampler, J., & Gaskell, C. M. 1989, ApJ, 338, 630
Boroson, T. A., & Green, R. F. 1992, ApJS, 80, 109
Burgess, A., & Tully, J. A. 1992, A&A, 254, 436
Clavel, J., & Santos-Lleo, M. 1990, A&A, 230, 3
Dere, K. P., Monsignori-Fossi, B. C., Landi, E., Mason, H. E., & Young, P. R. 1996, BAAS, 28, 961
Ferland, G. J., Baldwin, J. A., Korista, K. T., Hamann, F., Carswell, R. F., Phillips, M., Wilkes, B., & Williams, R. E. 1996, ApJ, 461, 683
Ferland, G. J., et al. 1995, in The Analysis of Emission Lines, ed. R. Williams & M. Livio (Baltimore, MD: STScI), 83
Ferland, G. J., Korista, K. T., Verner, D. A., Ferguson, J. W., Kingdon, J. B., & Verner, E. M. 1997, PASP, in press
Gaetz, T. J., & Salpeter, E. E. 1983, ApJS, 52, 155
Hamann, F., & Ferland G. J. 1992, ApJ, 391, L53
Hamann, F., & Ferland G. J. 1993, ApJ, 418, 11
Horne, K. 1994, in ASP Conf. Ser., Vol. 60, Reverberation Mapping of the Broad Line Region in Active Galactic Nuclei, ed. P. M. Gondhalekar, K. Horne, & B. M. Peterson (San Francisco: ASP), 23
Hummer, D. G., Berrington, K. A., Eissner, W., Pradhan, A. K., Saraph, H. E., & Tully, J. A. 1993, A&A, 279, 298
Kingdon, J. B., & Ferland G. J. 1996, ApJS, 106, 205
Korista, K., Baldwin, J., Ferland, G., & Verner, D. 1997, ApJS, 108, 401
La Franca, F., Franceshini, A., Cristiani, S., & Vio, R. 1995, A&A, 299, 19
Mewe, R. 1972, A&A, 20, 215
Osmer, P. A., Porter, A. C., & Green, R. F. 1994, ApJ, 436, 678
Veigele, W. J. 1973, Atomic Data Tables, 5, 51
Verner, D. A., & Ferland, G. J. 1996, ApJS, 103, 467
Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487
Verner, D. A., Verner, E. M., & Ferland, G. J. 1996, Atomic Data Nucl. Data Tables, 64, 1
Verner, D. A., & Yakovlev, D. G. 1990, Ap&SS, 165, 27
Worrall, D. M., Giommi, P., Tananbaum, H., & Zamorani, G. 1987, ApJ, 313, 596
Next: On Fractal Modeling in Astrophysics: The Effect of Lacunarity on the Convergence of Algorithms for Scaling Exponents.
Previous: Refined Simplex Method for Data Fitting
Up: Modeling
Table of Contents - Index - PS reprint - PDF reprint