
Next: A Method for Obtaining Reliable IRAS-LRS Data via the Groningen IRAS Server
Previous: Difmap: An Interactive Program for Synthesis Imaging
Up: Science Software Applications
Table of Contents - Index - PS reprint - PDF reprint
L. E. Davis
IRAF Group, NOAO,1 P.O. Box 26732, Tucson, AZ 85726
1National Optical Astronomy Observatories, operated by the Association of Universities for Research in Astronomy, Inc. (AURA) under cooperative agreement with the National Science Foundation
Centering algorithms are important to many astronomical applications. One dimensional (1-D) centering algorithms are used in spectral line detection, wavelength calibration, and radial velocity applications. Two dimensional (2-D) centering algorithms are used in object detection, image registration, photometry, and astrometry applications. The centering algorithms employed by these applications must satisfy a wide range of efficiency and accuracy requirements, and function robustly on data sets spanning a broad wavelength, resolution, and signal-to-noise regime. This paper presents an overview of CENTERFIT, a library of 1-D and 2-D centering algorithms currently under development in the IRAF system.
The CENTERFIT algorithms satisfy a broad range of scientific requirements. The algorithm choice was guided by the literature (Stone 1989; Lasker et al. 1990, and references therein) and by experience with existing IRAF centering routines. Algorithms optimized for efficiency (e.g., moment analysis), precision (e.g., functional fits to a Gaussian), and flexibility (e.g., functional fits to a SuperGaussian), are included. Wherever possible, 1-D and 2-D versions of the same algorithm are included, permitting efficiency versus precision tradeoffs on the part of the calling application (e.g., moment analysis of the marginals versus elliptical Gaussian fits to the original data). All of the CENTERFIT algorithms compute error estimates, and size, shape, and orientation information, where appropriate.
The CENTERFIT fitting routines are flexible. The calling applications can include or reject data from the fit, fix or fit the background value, impose minimum signal-to-noise criteria, fix or fit the values of selected function parameters (e.g., the Gaussian FWHM or the Moffat beta values), select one of several builtin weighting schemes, and set the fit convergence criteria.
The CENTERFIT library is self-contained. All of the required supporting algorithms, including a coarse centering algorithm, a selection of sky fitting algorithms, and a signal-to-noise estimation algorithm, are part of the CENTERFIT library. The required mathematics libraries are part of the IRAF core system MATH package.
The CENTERFIT library is easy to use. The number of interface routines is small, the calling sequences are simple, the algorithm parameters are initialized to reasonable default values and may be examined or reset at any time, image I/O and memory are managed internally, and all the routines return error information.
The CENTERFIT library also provides access to a set of numerical fitting routines, permitting applications to manage their own image I/O and memory requirements, and perform their own parameter initialization.
The CENTERFIT library is extensible. New centering and sky fitting algorithms can be added by writing the required low level routines, and making the appropriate entries in the algorithms.
The 1-D CENTERFIT algorithms operate directly on 1-D image data or on the marginal distributions derived from 2-D image data. The 1-D algorithms list includes: moment analysis, optimal centering with a sawtooth function, and fits to Gaussian, Moffat, and SuperGaussian functions (integrated and non-integrated). The 2-D CENTERFIT algorithms operate directly on 2-D image data. The 2-D algorithms list includes: moment analysis, and fits to elliptical Gaussian, Moffat, and SuperGaussian functions (integrated and non-integrated).
Function fitting is performed by minimizing the chi-squared statistic using the Levenberg-Marquardt non-linear least squares fitting algorithm. Three builtin weighting schemes are supported: uniform, noise, and 8-fold symmetry weighting (Lasker et al. 1990). Integrated function evaluation is performed using a four point Gauss-Legendre integration scheme (Abramowitz & Stegun 1970).
Several sky fitting algorithms are supported including: setting a constant sky value, direct computation of the mean and median of the sky pixel distribution, moment analysis and optimal centering of the sky pixel histogram, and fitting a planar sky.
The principal CENTERFIT interface routines are listed below. These routines are used to allocate and deallocate the CENTERFIT data structures, set and get the CENTERFIT algorithm parameters, locate an object, extract the image data, estimate the background value, and compute the center.

The following routines are examples of the 2-D numerical interface routines. These routines compute the weights, initialize the function parameters using 2-D moment analysis, and fit the selected function to the data using the Levenberg-Marquardt non-linear least squares fitting code.
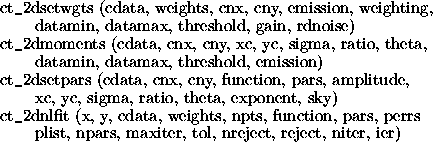
A comparisons of four of the most popular CENTERFIT algorithms: moment analysis of the marginals, Gaussian function fits to the marginals, radially symmetric Gaussian function fits to the data, and elliptical Moffat function fits to the data, was made using a 1024 pixel square artificial star field created with the IRAF ARTDATA package. The test field contained 500 stars uniformly distributed in position and in brightness over a 10 magnitude range. A radially symmetric Moffat function with FWHM = 2.0 pixels and beta = 2.5 was used to model the stars, and realistic Poisson and Gaussian read noise were added to the image.
For all four algorithms the bright object measurement precision was limited by the psf model template spacing (0.01 pixels) and sub-pixel gridding (10×10) to ~0.005 pixels. The three function fitting algorithms exceeded this expected accuracy with mean bright object measured (fitted - model) centering errors of ±~0.004 pixels. The 1-D moments algorithm performed significantly worse, with a mean bright object measured centering error of ±~0.009. The bright object predicted centering errors were limited by how well the assumed model fit the data. For the 1-D and radially symmetric Gaussian function fits, the predicted centering errors were much larger than the measured errors. By contrast, the bright object predicted centering errors for the model independent 1-D moments and elliptical Moffat function fitting algorithms were in reasonable agreement with the measured errors. Faint object measurement precision was limited by signal-to-noise, with the 2-D algorithms performing significantly, but not overwhelmingly, better than the equivalent 1-D algorithms, in agreement with Chiu (1977). The faint object predicted centering errors agree well with the faint object measured errors.
The four algorithms vary widely in efficiency, with the 1-D Gaussian, radially symmetric Gaussian, and elliptical Moffat function taking ~3.0, 6.4, and 13.1 times as long, respectively, as the 1-D moments algorithm, which required ~2.2 cpu seconds to fit 500 stars on a SPARCstation2.
For this particular data set, no significant improvement in the centering errors was obtained by using the integrated forms of the 1-D and 2-D Gaussian and 2-D Moffat functions. Better formal centering error values were obtained, but only at the expense of significantly increased execution times.
Coding and preliminary testing of the current CENTERFIT algorithm set is complete, although detailed numerical testing is still in progress. Future plans for the package include adding function fitting criteria other than chi-squared minimization, and fitting techniques other than the Levenberg-Marquardt algorithm.
Abramowitz, M., & Stegun, I. A. 1970, Handbook of Mathematical Functions (New York: Dover), 916
Chiu, L.-T. G. 1977, AJ, 82, 842
Lasker, B. M., Sturch, C. R., McLean, B. J., Russell, J. L., Jenkner, H., & Shara, M. M. 1990, AJ, 99, 2019
Stone, R. C. 1989, AJ, 97, 1227
Next: A Method for Obtaining Reliable IRAS-LRS Data via the Groningen IRAS Server
Previous: Difmap: An Interactive Program for Synthesis Imaging
Up: Science Software Applications
Table of Contents - Index - PS reprint - PDF reprint