
Next: Non-parametric Algorithms in Data Reduction at RATAN-600
Previous: A New Stable Method for Long-Time Integration in an N-Body Problem
Up: Algorithms
Table of Contents - Index - PS reprint - PDF reprint
Y. Chen, T. P. Li, and M. Wu
High Energy Astrophysics Lab, Institute of High Energy
Physics, Chinese Academy of Sciences,
Beijing 100039, PRC, E-mail: cheny@astrosv1.ihep.ac.cn
The imaging problem may be described as inferring the sky brightness distribution from observations and prior knowledge (Cornwell 1992). In this paper, we will introduce an optimizing method and adopt it to the imaging problem. Then we will apply it to simulations of a rotating modulation collimator (RMC), and ROSAT PSPC (the Position Sensitive Proportional Counter) observations.
The imaging problem is:

where d is the observational data, P is the point spread function, f is the unknown sky, and n is the noise. Usually, there are some constraints for f and n in this linear system of equations. The optimizing problem is:

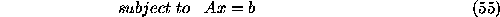

where 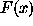 is an objective function.
is an objective function.
In astronomy, the noise 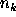 usually follows a Poisson or
Gaussian distribution. Thus it has a certain expected value and variance.
The sky intensity f may have
a upper limit up and a lower limit low.
Then we can make an objective
function
usually follows a Poisson or
Gaussian distribution. Thus it has a certain expected value and variance.
The sky intensity f may have
a upper limit up and a lower limit low.
Then we can make an objective
function
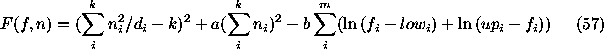
where a and b are coefficients, k is the number of bins of observational data, and m is the number of sky bins. The constraint condition is
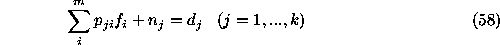
Both 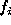 and
and 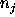 are unknown.
This problem is similar to the convex programming problem.
are unknown.
This problem is similar to the convex programming problem.
The affine scaling (AS) algorithm is one of the simplest and most efficient of interior point method algorithms (Dikin 1967). For the optimizing problem (2) ~ (4) the AS algorithm in detail is:
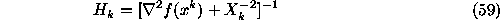
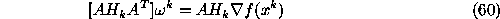
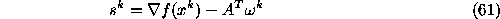

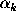 .
Search for that
.
Search for that 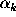 which
minimizes the objective function.
which
minimizes the objective function.
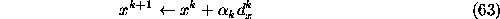
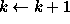 and go to Step 2.
and go to Step 2.
We developed an algorithm based on the affine scaling algorithm (Goldfarb 1991; Fang 1993) for problem (5) ~ (6).
We have simulated a rotating modulation collimator. The configuration
of the RMC is shown in Table 1.
The background is assumed to be 0.09 ph cm-2
s-1. The fluxes of the two point sources are assumed to be
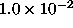 and
and 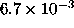 ph cm-2 s-1,
and the total flux of the extended source
ph cm-2 s-1,
and the total flux of the extended source 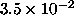 ph cm-2 s-1 (Figure 1a). The observing time is assumed
to be one day.
ph cm-2 s-1 (Figure 1a). The observing time is assumed
to be one day.

: The Configuration of the RMC
Figure 1b shows the result of the AS algorithm, while Figure 1c and d result from the cross-correlation method and the CLEAN cross-correlation, respectively. Both the point sources and the extended source can be seen in Figure 1b. The angular resolution and image quality in Figure 1b are much better than in the cross-correlation images.
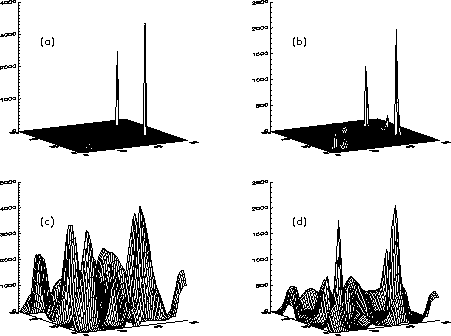
: a) The assumed sources. b) Result of the AS algorithm.
c) Result of cross-correlation. d) Result of CLEAN cross-correlation.
Original PostScript figure (392kB).
We used this algorithm to reconstruct ROSAT PSPC data. The results are shown in Figure 2. Figure 2a is the original image observed by PSPC. The result of the AS algorithm is shown in Figure 2b, where the extended structure is clearly seen. This extended structure can also be seen by ROSAT HRI (the High Resolution Imager) (Figure 2c).

Figure: a) The original ROSAT PSPC Crab nebula image.
b) The image obtained from the AS algorithm. The FOV is 100
× 100 arcsec. c) A ROSAT HRI image of the Crab nebula. The FOV is
100×96 arcsec.
Original Postscript figures(264kB), (264kB), and ().
The calculation time for the AS algorithm depends on the initial solution. We can use the solution, from some other algorithm such as Richardson-Lucy iteration or cross-correlation, as the initial solution in order to reduce the calculation time.
In this paper we developed an AS algorithm and applied it to the imaging problem. The results show that this algorithm can be used in the imaging problem and usually results in a better image than that obtained from a traditional method such as cross-correlation. This algorithm can be also used in the data reconstruction of an imaging instrument (e.g., ROSAT PSPC).
We thank X. J. Sun for the help on the ROSAT data analysis.
Cornwell, T. J. 1992, in Astronomical Data Analysis Software and Systems I, ASP Conf. Ser., Vol. 25, eds. D.M. Worrall, C. Biemesderfer, & J. Barnes (San Francisco, ASP), 163
Goldfarb, D., & Liu, S. 1991, Mathematical Programming, 49, 325
Fang, S.-C., & Puthenpura, S. 1993, in Linear Optimization and Extensions (Englewood Cliffs, NJ: Prentice Hall)
Next: Non-parametric Algorithms in Data Reduction at RATAN-600
Previous: A New Stable Method for Long-Time Integration in an N-Body Problem
Up: Algorithms
Table of Contents - Index - PS reprint - PDF reprint