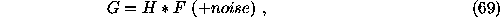
Next: Refined Simplex Method for Data Fitting
Previous: Generalized Spherical Harmonics for All-Sky Polarization Studies
Up: Algorithms
Table of Contents - Index - PS reprint - PDF reprint
M. I. Agafonov
Radiophysical Research Institute (NIRFI),
25 B. Pecherskaya st., Nizhny Novgorod, 603600, Russia,
E-mail: agfn@nirfi.nnov.su
Two dimensional image reconstruction from 1-D projections is often hampered by the small number of available projections, by an irregular distribution of position angles, and by position angles that span a range smaller than about 100°. These limitations are typical of both lunar occultations of celestial sources and observations with the fan beam of a radio interferometer, and also apply to greatly foreshortened reconstructive tomography.
The problem requires the solution of the equation
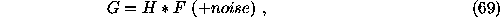
where 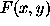 is the object brightness distribution,
is the object brightness distribution,
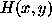 is the fan (dirty) beam, and
is the fan (dirty) beam, and 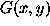 is the dirty (summary) image.
The classical case (Bracewell & Riddle 1967) needs a number of
projections
is the dirty (summary) image.
The classical case (Bracewell & Riddle 1967) needs a number of
projections 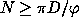 , where
, where 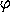 is the desired angular resolution,
and D is the diameter of the object. The incomplete sampling of
is the desired angular resolution,
and D is the diameter of the object. The incomplete sampling of 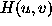 requires the extrapolation of the solution of
requires the extrapolation of the solution of  using non-linear
processing methods.
using non-linear
processing methods.
The general scheme of an iterative algorithm is
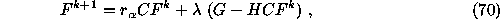
where
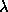 is the loop gain (
is the loop gain (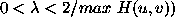 ,
,
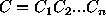 are the limitations, and
are the limitations, and 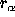 is the stabilizer.
is the stabilizer.
The simple standard CLEAN (Högbom 1974) is the best known realization of iteration schemes in radio astronomy. But the algorithm has defects (stripes and ridges) in areas of extended emission. CLEAN was used for the image reconstruction of the Crab Nebula from four lunar occultation profiles (Maloney & Gottesman 1979; Agafonov et al. 1986). However, more complete information is needed for an extended object. Trim Contour CLEAN (TC-CLEAN) (Steer et al. 1984) gave hope for the improvement of image quality with extended features, but it needed a study in different practical cases (Cornwell 1988).
The process of solution convergence by  (ERROR of initial
and control 1-D profiles) minimization with variation of parameters
(ERROR of initial
and control 1-D profiles) minimization with variation of parameters
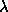 and TC (Trim Contour level) was investigated (Agafonov
& Podvojskaya 1989; Agafonov & Podvojskaya 1990) for both algorithms
using of the following procedure:
and TC (Trim Contour level) was investigated (Agafonov
& Podvojskaya 1989; Agafonov & Podvojskaya 1990) for both algorithms
using of the following procedure:
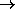 1-D profiles
1-D profiles 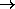 Dirty image
Dirty image
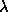 ) or TC-CLEAN (
) or TC-CLEAN (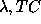 ) using
the Dirty beam
) using
the Dirty beam
 (ERROR of control and initial 1-D profiles)
(ERROR of control and initial 1-D profiles)
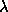 or
or 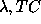 to
to 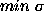
The process of parameter (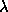 or
or 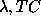 ) optimization
to
) optimization
to 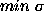 was shown very well graphically (Agafonov
& Podvojskaya 1989).
was shown very well graphically (Agafonov
& Podvojskaya 1989).
The dirty map peak is the target of each iteration. The choice of loop gain
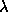 was not clear in the original scheme, but it significantly influences
the solution. For example, by modeling the test
object (Crab Nebula map at 1.4GHz) the optimum range of
was not clear in the original scheme, but it significantly influences
the solution. For example, by modeling the test
object (Crab Nebula map at 1.4GHz) the optimum range of 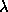 was
found to be about 0.05-0.10 (from the dependence of
was
found to be about 0.05-0.10 (from the dependence of 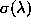 in this map). But the optimum value depends on the object structure.
The algorithm has high instability for distributed objects.
Changes in the resulting maps as a function of
in this map). But the optimum value depends on the object structure.
The algorithm has high instability for distributed objects.
Changes in the resulting maps as a function of  with small changes of
with small changes of 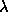 testifies to this
instability. We attempted to increase stability by: (i) choosing
solutions with
testifies to this
instability. We attempted to increase stability by: (i) choosing
solutions with 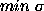 from the optimum interval and then
averaging; and (ii) by special processing-such as a complex method like
speckle-masking (but increasing the computational efforts).
from the optimum interval and then
averaging; and (ii) by special processing-such as a complex method like
speckle-masking (but increasing the computational efforts).
A smooth function is subtracted at each iteration. Trim contour
(TC) is used for the choice of components per iteration. TC must be low,
but
above the level corresponding to the true object dimensions. The algorithm
has high stability, a simple choice of 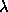 and TC, converges in
few iterations, and is computationally efficient.
and TC, converges in
few iterations, and is computationally efficient.
A simple object (consisting of the peaks) may be successfully restored by the standard CLEAN. The results obtained by both methods are practically identical for a simple object consisting of individual components, but TC-CLEAN is more computationally efficient. A difference between the solutions is observed for complicated objects with small components in areas of extended emission. The standard CLEAN reconstruction has a ``grooved'' structure for such areas.
For smoothed 1-D profiles with small ``hillocks,'' the solution can
be obtained from the isolated individual
components (CLEAN), and also from the more smoothed components (TC-CLEAN)
by using the same 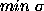 for the initial and control profiles.
CLEAN increases the contrast of small components, but the extended
background decreases because of the ``grooves.'' If
for the initial and control profiles.
CLEAN increases the contrast of small components, but the extended
background decreases because of the ``grooves.'' If 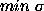 (CLEAN)
(CLEAN) 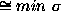 (TC-CLEAN),
the solutions will be formally equivalent for both algorithms, and so we have
two choices:
(i) to prefer the result corresponding to the physical peculiarities
of the object in accordance with a priori information; or
(ii) to assume the existence of a probable class of solutions between the
``obtuse'' (smooth) one from TC-CLEAN and the ``sharp'' one from CLEAN.
(TC-CLEAN),
the solutions will be formally equivalent for both algorithms, and so we have
two choices:
(i) to prefer the result corresponding to the physical peculiarities
of the object in accordance with a priori information; or
(ii) to assume the existence of a probable class of solutions between the
``obtuse'' (smooth) one from TC-CLEAN and the ``sharp'' one from CLEAN.
CLEAN forms the solution from the sum of peaks, and the result is the sharpest variant permissible within the established constraints. On the other hand, TC-CLEAN accumulates its result from the most extended components that satisfy the constraints, producing the smoothest solution (Agafonov & Podvojskaya 1990).
We carried out the study of TC-CLEAN applied to image reconstruction with few projections. TC-CLEAN proved to be an effective and stable solution. CLEAN emphasizes only individual features and needs a special treatment to obtain the solution stability (except the object from the peaks). We suggest determining the area of permissible solutions of complicated objects with the help of both algorithms. This procedure was named 2-CLEAN Determination of Solution Area (2-CLEAN DSA). It is also useful to study the possibility of reconstruction (the reality of the components on the map) for any new case with poor UV-filling by using a similar method used for our observational test object. The 2-CLEAN DSA procedure can show, in complicated cases, a range of possible images from ``obtuse'' to ``sharp'' variants satisfying imposed constraints and poor a priori information.
In certain cases, usually at lower frequencies, the angular resolution of synthesis radio telescopes is insufficient. However, observations of an object during lunar occultations provide 1-D brightness profiles with high angular resolution. This is also useful in observations with optical instruments. The lunar limb is approximated by a plane screen, moving through different position angles. The first images of the Crab Nebula from four projections of lunar occultations was presented by using the standard CLEAN (Maloney & Gottesman 1979; Agafonov et al. 1986). But the maps had defects in extended areas due to the reconstruction algorithm. The application of TC-CLEAN was used in the reconstruction of the Crab Nebula map at 750MHz with angular resolution 20×35´´ (Agafonov et al. 1990). The 1-D profiles were obtained by observations using the 70meter dish (RT-70) in West Crimea. The method of 2-CLEAN DSA allowed us to determine that the area of permissible solutions lies formally between the ``sharp'' (CLEAN) and ``smooth'' (TC-CLEAN) variants. The two maps were generally similar. The standard CLEAN increased the contrast of small components, while the TC-CLEAN map gave a better agreement with known a priori information about the Nebula, and was closer to the true brightness distribution of the Crab. The CLEAN variant of the map can be used only for information about the location of the small components.
I am grateful to the National Radio Astronomy Observatory for the support which made possible this presentation and my special gratitude to R. Simon and C. White for their endurance in the organization of this Conference.
Agafonov, M. I., Aslanyan, A. M., Gulyan, A. G., Ivanov, V. P., Martirosyan, R. M., Podvojskaya, O. A., & Stankevich, K. S. 1986, Pis'ma v AZh, 12, 275
Agafonov, M. I., & Podvojskaya, O. A. 1989, Izvestiya VUZ. Radiofizika, 32, 742
Agafonov, M. I., & Podvojskaya, O. A. 1990, Izvestiya VUZ. Radiofizika, 33, 1185
Agafonov, M. I., Ivanov, V. P., & Podvojskaya, O. A. 1990, AZh, 67, 549
Bracewell, R. N., & Riddle, A. C. 1967, ApJ, 150, 427
Cornwell, T. J. 1988, A&A, 202, 316
Högbom, J. A. 1974, A&AS, 15, 417
Maloney, F. P., & Gottesman, S. F. 1979, ApJ, 234, 485
Steer, D. G., Dewdney, P. E., & Ito, M. R. 1984, A&A, 137, 159
Next: Refined Simplex Method for Data Fitting
Previous: Generalized Spherical Harmonics for All-Sky Polarization Studies
Up: Algorithms
Table of Contents - Index - PS reprint - PDF reprint