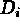 as the original pixel value,
as the original pixel value, 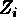 the zero level,
the zero level,
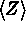 the average of
the average of 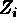 ,
, 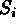 the divisive scaling
factor,
the divisive scaling
factor, 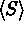 the average
of
the average
of 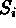 , and
, and 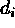 the scaled pixel value, we write
the scaled pixel value, we write
C. Y. Zhang
Space Telescope Science Institute, 3700 San Martin Dr.,
Baltimore, MD 21218
In images taken with CCD cameras, cosmic ray (CR) events become a common and annoying problem. Space-based CCD cameras, such as the Wide Field/Planetary Camera (WFPC) of the Hubble Space Telescope ( HST), are especially subject to a large flux of CR events. The problem becomes even more prominent for the new WFPC2. In these cases, it is recommended that long science observations be broken into at least two exposures (CR-SPLIT) to ensure that CR events can later be identified and removed (see, e.g., Wide Field and Planetary Camera 2 Instrument Handbook, 1994).
The task GCOMBINE, in STSDAS, is designed mainly for HST images in GEIS format, but is not restricted to them. A parameter, groups, allows a user to select a range of groups to combine. A combined image is either a weighted average or median of a set of input images with bad pixels, including CR events, removed. As in the IRAF task IMCOMBINE, bad pixels can be rejected using masking, threshold levels, and various rejection algorithms.
A list of input error images can be used for the algorithm, errclip to reject bad pixels and to compute the pixel-wise weight when the parameter, weight, is set to pixelwise.
There are a variety of rejection algorithms from which to choose for rejecting bad pixels after possible masking and thresholding operations. These are the minmax, ccdclip, rsigclip, avsigclip, and the errclip algorithms. In the following, we will discuss some of these algorithms in more detail.
In order to combine images with different exposures, one must first bring them
to a common level. For the i'th image, let us denote
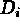 as the original pixel value,
as the original pixel value, 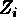 the zero level,
the zero level,
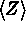 the average of
the average of 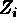 ,
, 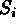 the divisive scaling
factor,
the divisive scaling
factor, 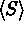 the average
of
the average
of 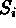 , and
, and 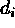 the scaled pixel value, we write
the scaled pixel value, we write
This will bring the images to the mean sky level of
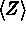 and common exposure level of
and common exposure level of 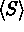 .
In the code, Equation (1) is translated into
.
In the code, Equation (1) is translated into
where 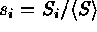 and
and
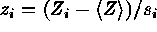 . The normalized
scaling factors
. The normalized
scaling factors 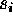 and
and 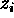 are stored in an output log file.
are stored in an output log file.
When the combined image is defined as a weighted average, it is useful to distinguish between uniform and pixelwise weighting schemes. By pixelwise weighting, we mean that the weight is calculated on a pixel-by-pixel basis. It requires an input ``error map'' associated with each input image, and the weight factor at a given pixel is then calculated as a reciprocal of the square of the error at that pixel. By uniform weighting, we mean that the weight is a constant for all pixels in an input image. In the case of uniform weighting, one has a variety of choices, such as, the exposure time, the mean, median, or mode of the input image. In a relatively flat image, one may choose a reciprocal of an averaged variance as a uniform weight.
After a mean is computed, one computes a deviation
of the pixel from the mean and then compares it with a ``clipping
sigma''. If the deviation exceeds a specified threshold, 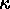 ,
times the clipping sigma, then the pixel under test is regarded as being bad.
After the bad pixel is rejected, one iterates the process, but now the
mean and the clipping sigma are re-calculated, excluding the bad pixels
already rejected in the previous iterations. This iteration terminates
when no more pixels are rejected or the retained number of pixels is
fewer than the user-specified minimum number of retained pixels.
,
times the clipping sigma, then the pixel under test is regarded as being bad.
After the bad pixel is rejected, one iterates the process, but now the
mean and the clipping sigma are re-calculated, excluding the bad pixels
already rejected in the previous iterations. This iteration terminates
when no more pixels are rejected or the retained number of pixels is
fewer than the user-specified minimum number of retained pixels.
It is obvious that if there are outliers to be identified, the simple mean of all measurements not excluding the unidentified outliers will be significantly biased by often too large values of the outliers. The effects of the unidentified outliers on the estimate of the clipping sigma could be even more severe, since the deviation is being squared in computing the sigma. We discuss the robust sigma clipping algorithm, rsigclip, in detail.
Assuming the Poisson noise dominates
over the read noise, and, for simplicity, ignoring the effects of the
zero flux level offset, Equation (2) is reduced to 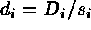 .
The sigma in the scaled image becomes,
.
The sigma in the scaled image becomes,
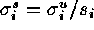 ,
where
,
where 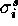 and
and 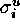 are the sigmas corresponding
to the scaled and unscaled data. For the Poisson distribution,
are the sigmas corresponding
to the scaled and unscaled data. For the Poisson distribution,
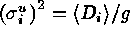 ,
where g is the gain. The optimal mean of the unscaled data is given by
,
where g is the gain. The optimal mean of the unscaled data is given by
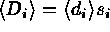 ,
where
,
where 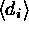 is the proper mean of the scaled data.
We thus have,
is the proper mean of the scaled data.
We thus have,
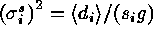 .
Therefore, even if the gain is unknown, the relative variance,
.
Therefore, even if the gain is unknown, the relative variance,
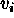 , in the scaled data is given by
, in the scaled data is given by 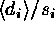 .
Taking the weights
.
Taking the weights 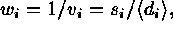 the average sample sigma is given by
the average sample sigma is given by
Noting that 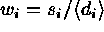 , the estimated absolute value
of the sigma in the scaled data is then given (see, e.g., Bevington 1969) by
, the estimated absolute value
of the sigma in the scaled data is then given (see, e.g., Bevington 1969) by
where the Poisson scaling factor is given by 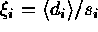 .
.
It is emphasized that no matter how accurate Equation (4) is when the data follow exactly the Poisson distributions, the presence of unidentified outliers, which do not follow the same Poisson statistics at all, will inevitably make the estimates of Equation (4) unrealistic. It is where the ``robust'' estimation of the mean and sigma should come into play.
The method for estimating the mean used in rsigclip is robust. We exclude the maximum and minimum values before computing the mean, because they are most vulnerable to being bad. The effect is to assign a zero weight to the two extremal points, while assigning normal weights to the rest of data. This estimation of the so-called trimmed mean, used in the GCOMBINE and IMCOMBINE tasks, is an estimate of the mean robust against unidentified outliers.
To minimize influence of unidentified outliers on the clipping sigma,
Equation (3) is modified. We set a ``normal'' range of the data values to
exclude the most deviant points on both sides from the mean. For
points that are within the range, the normal weights,
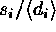 ,
are used, as in Equation (3). Much smaller weights are assigned to the
points outside of the range, farther from the mean:
a weight of
,
are used, as in Equation (3). Much smaller weights are assigned to the
points outside of the range, farther from the mean:
a weight of 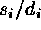 is used
for points on the high side of the mean,
and a weight of 0.001
is used
for points on the high side of the mean,
and a weight of 0.001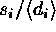 is applied to points on the low side
of the mean. An outlier, if present, will get the negligible weight
and therefore have minimal influence on the clipping
is applied to points on the low side
of the mean. An outlier, if present, will get the negligible weight
and therefore have minimal influence on the clipping  .
This scheme works fine for identifying CR events, even in the case
of only a few images to combine.
.
This scheme works fine for identifying CR events, even in the case
of only a few images to combine.
If the noise in the i'th unscaled image can be obtained from the
CCD noise model, using the error propagation principle and the
relation that 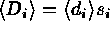 , we
find that the optimal clipping sigma in the scaled image should be
, we
find that the optimal clipping sigma in the scaled image should be
where 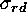 is the readout noise in number of electrons, g
is the gain factor in units of
is the readout noise in number of electrons, g
is the gain factor in units of 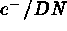 , and s is the fractional
``sensitivity noise.''
, and s is the fractional
``sensitivity noise.''
In the code, the trimmed mean or median is used. Substituting the trimmed mean or median into Equation (5) gives estimation of the clipping sigma. This clipping sigma does not involve in any computations of the square of the deviations, is thus robust against the unidentified outliers. If the error maps exist for input images, one does not have to compute the clipping sigma, because the sigma is available from the input error maps for each individual pixels. The testing shows that errclip works well for WFPC images. if one makes error maps using, e.g., the imcalc task based on the CCD noise model. In doing so, it is important that the error provided in the input error maps should simultaneously be scaled as the input images.
In the above discussions, only the information along a stack of input images for a given output pixel is used. It is conceivable that information in neighboring pixels, such as patterns of various astronomical objects, can be used to distinguish CR events. In the case of, say, only two images to combine, it becomes mandatory to use as much of the information in the image plane as possible. In the GCOMBINE task the information contained in the neighboring pixels is globally taken into account for the case of two images to combine.
It is conceivable that the pixel values of the two images for the same
target, through the same filter, must be closely correlated with each
other. If one plots pixel values of one image versus those of the
other, it is seen that more than 99.5% pixels are located in between
the two envelope curves, where the pixel values of one image equal
those of the other plus and minus three sigma.
The outliers are almost exclusively located outside the enveloped
region. The locations of outliers relative to the rest of
neighboring ``normal'' pixels show in a global way that
it is possible to identify outliers based on the direct difference
of the pixel values of the two images at a given pixel of the combined
image. If the difference exceeds the user-specified 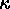 times
of the sigma, the larger one
is rejected as long as the very negative pixels are excluded first.
The clipping sigma, in this case, can only be obtained with either
the CCD noise model or the input error map.
Tests show that this method is very effective in removing cosmic rays.
times
of the sigma, the larger one
is rejected as long as the very negative pixels are excluded first.
The clipping sigma, in this case, can only be obtained with either
the CCD noise model or the input error map.
Tests show that this method is very effective in removing cosmic rays.
I am grateful to F. Valdes, R. White, and K. Ratnatunga for very stimulating discussions.
Burrows, C. J., ed. 1994, Wide Field and Planetary Camera 2 Instrument Handbook (Baltimore, Space Telescope Science Institute)