



 64 kB PostScript reprint
64 kB PostScript reprint
Next: Statistical Analysis
Up: Image Restoration and
Previous: Restoration of HST
Astronomical Data Analysis Software and Systems IV
ASP Conference Series, Vol. 77, 1995
Book Editors: R. A. Shaw, H. E. Payne, and J. J. E. Hayes
Electronic Editor: H. E. Payne
N. Wu
Space Telescope Science Institute, 3700 San Martin Drive,
Baltimore, MD 21218
Abstract:
This presentation is devoted to the MEM (Maximum Entropy Method) task,
version D, for image restoration in IRAF. Described in detail are its
enhanced functions of Poisson noise only case handling and subpixelization
technique; improved algorithms for maximization including the preconditioned
conjugate method, accurate Newton method, the accurate one-dimensional search,
and the model updating technique. The task's limitations and possible
development are also discussed.
The IRAF mem0 package, version B, was released to the public in
October 1992, and was upgraded to version C in December 1993. Version C
resides in the anonymous ftp site at NOAO ( iraf.noao.edu, directory
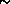 /contrib/).
Now, the most important MEM task of the mem0 package has been
upgraded to version D; the other four tasks remain unchanged.
This task is included in the subpackage stsdas.analysis.restore
with the name mem. Its executable code on SUN/UNIX has also been put
into the ftp site at NOAO with the task name dmem. The two relevant
files are dmem.notes and dmem.tar.Z.
/contrib/).
Now, the most important MEM task of the mem0 package has been
upgraded to version D; the other four tasks remain unchanged.
This task is included in the subpackage stsdas.analysis.restore
with the name mem. Its executable code on SUN/UNIX has also been put
into the ftp site at NOAO with the task name dmem. The two relevant
files are dmem.notes and dmem.tar.Z.
The task mem, version D, features the following sophisticated
functions and techniques:
- Poisson noise only case handling.
- Subpixelization technique.
- Model updating technique.
- The preconditioned conjugate method and accurate Newton method.
- The accurate one-dimensional search in maximization.
They are described in detail in the following section.
CCD images from the Wide Field and Planetary Camera (WF/PC) of
Hubble Space Telescope ( HST) have both readout noise, of Gaussian type, and
signal noise, of Poisson type. In this case the total noise variance is
calculated using the parameters noise, in electrons, for the former,
and adu (analogue-to-digital unit conversion constant or gain),
in electrons/DN, for the latter. Then this variance is used in the
Gaussian likelihood function or, equivalently, in the expression of
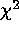 .
.
On the other hand, images from the photon counting detectors of the Faint
Object Camera (FOC) of HST contain only signal noise of Poisson type.
Not only should the parameter noise be set to zero,
but, more importantly, the Poisson likelihood function
must be used in calculation. Failure to do so will lead to wrong and
unacceptable results.
Earlier versions of the task mem could not handle correctly the case of
Poisson noise only.
In version D, setting the parameter poisson to yes
selects the correct expression for the likelihood function, automatically
sets the parameter noise to zero, and takes other actions
especially designed for the case of Poisson noise only.
It has been shown that the subpixelization (subsampling) technique
may improve resolution in restored images, or at least result in more
pleasant appearances for objects (Weir & Djorgovski 1990).
Subpixelization means to restore an image on a grid finer than
that on which the input data image is defined.
In this process one ``normal size'' pixel of the input image is ``split''
to several ``subpixels'' of the restored image.
This mechanism must be built into the program, but cannot be accomplished
simply by replicating each pixel of the input image before restoration.
Subpixelization is activated by setting the parameter nsub
to a value greater than one. In this case all input images, including
the point spread function (PSF) but excluding the data image, must be
subpixelized by the user by a factor of nsub in each dimension.
The required core memory and computational time are approximately
proportional to nsub .
.
This technique was described in detail in Wu (1994).
The MEM program uses a double iteration scheme: the values of the
Lagrange multipliers 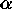 and
and 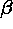 , respectively for
the data constraint and the total power constraint, are revised
in the outer iteration, while the inner iteration is
for finding the ME solution for the particular
, respectively for
the data constraint and the total power constraint, are revised
in the outer iteration, while the inner iteration is
for finding the ME solution for the particular 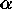 and
and
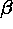 of each outer iteration.
of each outer iteration.
The basic idea behind the model updating technique is to use the ME image
converged for particular 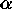 and
and 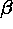 in each outer iteration as
the model to start the next iteration. In this way in maximization,
the approximate solution to the linear equations used in the
preconditioned conjugate method is more accurate, or the accurate solution
to the linear equations required in the accurate Newton method is
easier to be found. Therefore, the total number of iterations is
considerably reduced and much computational time is saved.
The restored image also has improved photometric linearity.
in each outer iteration as
the model to start the next iteration. In this way in maximization,
the approximate solution to the linear equations used in the
preconditioned conjugate method is more accurate, or the accurate solution
to the linear equations required in the accurate Newton method is
easier to be found. Therefore, the total number of iterations is
considerably reduced and much computational time is saved.
The restored image also has improved photometric linearity.
In previous versions of the task mem, only the zeroth-order approximate
Newton method of maximization was available. Hence the name of the package:
mem0. Zeroth-order approximation means that in the solution of a large
set of linear equations (or equivalently the inversion of a large
matrix) non-diagonal elements are ignored, under the assumption
that the diagonal ones dominate. In this way, solving the equations
becomes a simple operation. However, this simple method may result in
very slow convergence.
Now, in version D, much more sophisticated methods are used to calculate
the change in the iteration, i.e., to determine the search direction in
maximization.
The first method is the preconditioned conjugate method (as opposed to
the ``standard'' conjugate method commonly used), or the conjugate
method based on the approximate Newton method described in the above.
More specifically, in each outer iteration for particular 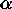 and
and
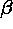 , the approximate Newton method is used to calculate
the search direction for the first inner iteration. Thereafter,
in each inner iteration, a direction is calculated using the
approximate Newton method. The component orthogonal or conjugate to
the search direction used in the previous inner iteration is calculated,
and used as the new search direction for the maximum point.
By careful programming, the core memory requirement and the number of FFTs
are the same as in the approximate Newton method.
, the approximate Newton method is used to calculate
the search direction for the first inner iteration. Thereafter,
in each inner iteration, a direction is calculated using the
approximate Newton method. The component orthogonal or conjugate to
the search direction used in the previous inner iteration is calculated,
and used as the new search direction for the maximum point.
By careful programming, the core memory requirement and the number of FFTs
are the same as in the approximate Newton method.
The second method is the accurate Newton method (as opposed to the approximate
Newton method). Here the accurate solution to a set of linear equations
of large size is calculated by iteration, each of which requires
two convolutions, i.e., four FFTs.
The accurate Newton method is the most efficient in the sense that
the fewest total number of (inner) iterations is needed because
the search direction is determined accurately.
However, many FFTs may well be required in each (inner) iteration
to solve the linear equations.
In contrast, the preconditioned conjugate method requires a greater
total number of (inner) iterations, but no extra FFTs in each
(inner) iteration are needed to calculate the conjugate direction.
By default, in the case of Poisson noise only ( poisson=yes)
the accurate Newton method is used, otherwise ( poisson=no)
the preconditioned conjugate method is used.
This is the best choice. In the case of Poisson noise only,
the Hessian of the objective function, which is a measure of the
curvature of the image space, changes rapidly from (inner)
iteration to iteration. Consequently, the preconditioned conjugate method,
as a method taking advantage of memory in the iteration, is not effective
in determining the search direction.
After determining the search direction, an optimal step (length)
in this direction should be calculated. In earlier versions of
the task mem, quadratic extrapolation
and cubic interpolation are used for this purpose. They are both
approximate methods for calculating the optimal step.
Now, in version D, the accurate one-dimensional (1-D) search is available for
interpolation. Specifically, the approximate maximum point found by
cubic interpolation is used as the initial guess to start a
search for the accurate maximum point, using the Newton method
in a single variable. In such a way, the maximum point is found with
little extra effort but much higher accuracy.
The (approximate) quadratic extrapolation remains. In most cases, especially
at the late stage of iteration, interpolation but not extrapolation
is desirable in the 1-D search.
Apart from employing the methods described in the previous subsections to
enhance the task's function and to speed up convergence,
having a good user interface is also important.
Every effort has been made to create a user friendly interface.
The number of positional parameters is kept to a minimum.
The default values of hidden parameters are carefully chosen.
Automatic schemes to adjust some variables
and to deal with some predicted ill-conditioned cases are built in the
program.
Options and parameters used only for testing are hidden from the user.
The diagnostic messages are informative and grouped logically, and can be
output at three different levels of verboseness to meet the user's needs.
The most detailed level ( message=3) is primarily for debugging
purposes.
The help file is well written and should be read
before the first attempt to run the task.
The current version of the task mem has its limitations:
Like other MEM programs, it
can only handle the case of space-invariant PSF.
It cannot be used for multi-channel and multi-data set restoration like
the package MEM/MemSys5 (Weir 1991).
The algorithm used in the accurate Newton method
to find the accurate solution of a large set of linear equations
should be improved, e.g., using the preconditioned conjugate method.
Finally, criteria for convergence should be investigated,
especially in the case of Poisson noise only, and more reasonable
ones should be adopted. For this version of the task, the user's
judgment is very important in obtaining satisfactory results.
References:
Weir, N. & Djorgovski, S. 1990, in The Restoration of
HST Images and Spectra, ed. R. L. White & R. J. Allen (Baltimore,
Space Telescope Science Institute), p. 31
Weir, N. 1991, in Proceedings of the 3rd ESO/ST-ECF
Data Analysis Workshop, ed. P. J. Grosbøl & R. H. Warmels
(Garching, ST-ECF), p. 115
Wu, N. 1994, in The Restoration of HST Images and Spectra II,
ed. R. J. Hanisch & R. L. White (Baltimore,
Space Telescope Science Institute), p. 58




 64 kB PostScript reprint
64 kB PostScript reprint
Next: Statistical Analysis
Up: Image Restoration and
Previous: Restoration of HST
adass4_editors@stsci.edu
 /contrib/).
Now, the most important MEM task of the mem0 package has been
upgraded to version D; the other four tasks remain unchanged.
This task is included in the subpackage stsdas.analysis.restore
with the name mem. Its executable code on SUN/UNIX has also been put
into the ftp site at NOAO with the task name dmem. The two relevant
files are dmem.notes and dmem.tar.Z.
/contrib/).
Now, the most important MEM task of the mem0 package has been
upgraded to version D; the other four tasks remain unchanged.
This task is included in the subpackage stsdas.analysis.restore
with the name mem. Its executable code on SUN/UNIX has also been put
into the ftp site at NOAO with the task name dmem. The two relevant
files are dmem.notes and dmem.tar.Z.
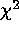 .
.
 .
.
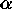 and
and 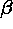 , respectively for
the data constraint and the total power constraint, are revised
in the outer iteration, while the inner iteration is
for finding the ME solution for the particular
, respectively for
the data constraint and the total power constraint, are revised
in the outer iteration, while the inner iteration is
for finding the ME solution for the particular 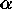 and
and
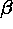 of each outer iteration.
of each outer iteration.
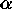 and
and 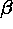 in each outer iteration as
the model to start the next iteration. In this way in maximization,
the approximate solution to the linear equations used in the
preconditioned conjugate method is more accurate, or the accurate solution
to the linear equations required in the accurate Newton method is
easier to be found. Therefore, the total number of iterations is
considerably reduced and much computational time is saved.
The restored image also has improved photometric linearity.
in each outer iteration as
the model to start the next iteration. In this way in maximization,
the approximate solution to the linear equations used in the
preconditioned conjugate method is more accurate, or the accurate solution
to the linear equations required in the accurate Newton method is
easier to be found. Therefore, the total number of iterations is
considerably reduced and much computational time is saved.
The restored image also has improved photometric linearity.
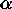 and
and
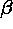 , the approximate Newton method is used to calculate
the search direction for the first inner iteration. Thereafter,
in each inner iteration, a direction is calculated using the
approximate Newton method. The component orthogonal or conjugate to
the search direction used in the previous inner iteration is calculated,
and used as the new search direction for the maximum point.
By careful programming, the core memory requirement and the number of FFTs
are the same as in the approximate Newton method.
, the approximate Newton method is used to calculate
the search direction for the first inner iteration. Thereafter,
in each inner iteration, a direction is calculated using the
approximate Newton method. The component orthogonal or conjugate to
the search direction used in the previous inner iteration is calculated,
and used as the new search direction for the maximum point.
By careful programming, the core memory requirement and the number of FFTs
are the same as in the approximate Newton method.