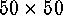 or
or
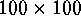 ). On computational grounds, a pure agglomerative
strategy is eminently feasible.
). On computational grounds, a pure agglomerative
strategy is eminently feasible.
F. Murtagh
Space Telescope -- European Coordinating Facility,
European Southern Observatory, Karl-Schwarzschild-Str. 2,
D-85748 Garching, Germany
Affiliated to Astrophysics Division, Space Science Department,
European Space Agency
The Kohonen self-organizing feature map (SOFM) method may be described in these terms (Kohonen 1988; Kohonen 1990; Kohonen et al. 1992; Murtagh & Hernández-Pajares 1994; Hernández-Pajares et al. 1994): each item in a multidimensional input data set is assigned to a cluster center; the cluster centers are themselves ordered by their proximities; and the cluster centers are arranged in some specific output representational structure, often a regularly-spaced grid. The output representational grid of cluster centers is structured through the imposition of neighborhood relations. Different variants on this algorithm are possible. A description of our exact, coded implementation may be found in Murtagh & Hernández-Pajares (1994). The regularly-spaced grid leads to a close relationship with a range of widely-used dimensionality-reduction methods (Sammon nonlinear multidimensional scaling, principal components analysis, etc.). The given dimensionality m is mapped into a discretised 2-dimensional space.
A practical problem arises with this SOFM method: if a two- or three-cluster solution is potentially of interest, it is difficult to specify an output representational grid with just this number of cluster centers. One would be more advised to use a traditional k-means partitioning method. Alternatively, the thought comes to mind to further process the cluster centers, perhaps in a way which is motivated by hierarchical cluster analysis. This is close to the graphical proposals of Ultsch (1993a, 1993b).
Cluster centers are formed by the SOFM method in such a
way that similarly-valued cluster centers are closely located on the
representational grid. This reinforces the need for any subsequent
clustering of these cluster centers to take such contiguity information
into account.
Contiguity-constrained clustering
has been reviewed by Murtagh (1985a),
Gordon (1981), and Murtagh (1994). Split-and-merge techniques may well be
warranted for segmenting large images. We however seek to segment a grid,
at each element of which we have a multidimensional vector, which is
ordinarily not of very large dimensions (say, if square, 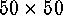 or
or
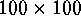 ). On computational grounds, a pure agglomerative
strategy is eminently feasible.
). On computational grounds, a pure agglomerative
strategy is eminently feasible.
A contiguity-constrained enhancement on such algorithms is to only
allow objects x and y to be agglomerated if in
addition we have: there is some 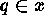 and some
and some 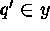 such that
q and
such that
q and 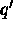 are contiguous. The definition of contiguity on the regular
grid is immediate if we require, for example, that the 8 possible
neighbors of a given grid intersection form contiguous neighbors.
are contiguous. The definition of contiguity on the regular
grid is immediate if we require, for example, that the 8 possible
neighbors of a given grid intersection form contiguous neighbors.
A number of theoretical and practical issues arise in the context of such algorithms. Such issues include the following which are discussed in Murtagh (1994):
The IRAS Point Source Catalog ( IRAS PSC) contains measurements on 245,897 objects. Coarse selection criteria, based on flux values or combinations of them, have been used for separating stars from non-stellar objects. Among non-stellar objects, in some studies, classes such as the three following ones have been distinguished: thin Galaxy plane; a ``cirrus'' region of objects surrounding this, due to dust; and the extragalactic sky. When using different normalizations of the input data, and different agglomerative criteria, we used this prior information (see Prusti et al. 1992; Boller et al. 1992; Meurs & Harmon 1988) to select one result over others.
No preliminary selections were made: all 245,897 objects were used.
A set of four variables was derived
from the four flux values (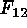 ,
, 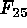 ,
, 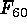 ,
, 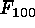 ), in line
with the studies cited above:
), in line
with the studies cited above: 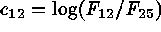 ,
,
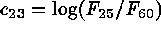 ,
, 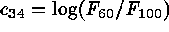 , and
, and
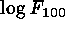 . The first three of these define intrinsic colors.
The SOFM method was applied to this
. The first three of these define intrinsic colors.
The SOFM method was applied to this 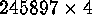 array, mapping it onto
a regular
array, mapping it onto
a regular 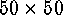 representational grid. This output can be
described as 2500 clusters (defined by a minimum distance criterion, similar
to k-means methods); with the cluster centers themselves located on the
discretized plane in such a way that proximity reflects similarity.
representational grid. This output can be
described as 2500 clusters (defined by a minimum distance criterion, similar
to k-means methods); with the cluster centers themselves located on the
discretized plane in such a way that proximity reflects similarity.
Normalization of the input data (necessitated, if for no other reason, by the fourth input being quite differently-valued compared to the first, second and third), was carried out in two ways: range-normalizing, by subtracting the minimum, and dividing by maximum minus minimum (this approach is favored in Milligan & Cooper 1988); or by carrying out a preliminary correlation-based principal components analysis (PCA). Three principal component values were used as input, for each of the 245,897 objects. Such normalizing is commonly practiced but is viewed negatively e.g., in Chang (1983), since mapping into a principal component space may destroy the classificatory relationships which are in fact sought. However, we found that this provided what we considered as the best end-result.
In all cases, the SOFM result was obtained following 10 epochs, i.e., all objects were successively cycled through 10 times. Typical computation times were 9 hours on a loaded SPARCstation 10. All other operations described in this paper (contiguity-constrained clustering, display, etc.) required orders of magnitude less time.
The numbers of
objects assigned to each of the 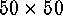 cluster centers were not taken
into account when carrying out the segmentation of this grid. We
chose 8 clusters as a compromise between having some information about a
desired set of 3 or 4 clusters (cf. discussion above regarding stars, thin
plane, cirrus and extragalactic classes);
and convenience in representing a somewhat
greater number of clusters.
Results obtained are further discussed in the more complete version
accompanying this paper: see next section for access details.
cluster centers were not taken
into account when carrying out the segmentation of this grid. We
chose 8 clusters as a compromise between having some information about a
desired set of 3 or 4 clusters (cf. discussion above regarding stars, thin
plane, cirrus and extragalactic classes);
and convenience in representing a somewhat
greater number of clusters.
Results obtained are further discussed in the more complete version
accompanying this paper: see next section for access details.
The combined SOFM-CCC approach provides a convenient framework for clustering. We have noted how the CCC approach is the most appropriate for SOFM output. To aid in interpretation of such a method, the use of tracer objects has been found to be very advantageous (Hernández-Pajares et al.\ 1994).
Large astronomical catalogs are common-place, and the IRAS PSC is not untypical. Unsupervised classification has often taken the form of ``hand-crafted'' approaches, e.g., through pairwise plots of variables and the visually-based specification of discrimination rules. Our aim is to have reasonably standard, automated approaches for handling such data. We do not wish to have major ``fault lines'' running through our methodology, but seek instead an integrated, cohesive framework.
Open issues are (1) further study of the input data normalization issues; and (2) the enhancement of the method described here to handle input data which have associated quality/error values and/or which are censored.
Chang, W. C. 1983, Appl. Stat., 32, 267
Gordon, A. D. 1981, Classification: Methods for the Exploratory Analysis of Multivariate Data (London, Chapman and Hall)
Hernández-Pajares, M., Floris, J., & Murtagh, F. 1994, Vistas in Astronomy, in press
Kohonen, T. 1988, in Proc. Connectionism in Perspective: Tutorial (Zurich, University of Zurich)
Kohonen, T. 1990, Proc. IEEE, 78, 1464
Kohonen, T., Kangas, J., & Laaksonen, J. 1992, SOM_PAK Version 1.0. Available by anonymous ftp from cochlea.hut.fi (130.233.168.48)
Meurs, E. J. A., & Harmon, R. T. 1988, A&A, 206, 53
Milligan, G. W., & Cooper, M. C. 1988, Journal of Classification 5, 181
Murtagh, F. 1985a, The Computer Journal, 28, 82
Murtagh, F. 1985b, Multidimensional Clustering Algorithms (Würzburg, Physica-Verlag)
Murtagh, F. 1994, in Partitioning Data Sets eds. I. J. Cox, P. Hansen and B. Julesz (New York, AMS), in press.
Murtagh, F. 1994, Pattern Recognition Letters, submitted
Murtagh, F., & Hernández-Pajares, M. 1994, Journal of Classification, in press
Research Systems, Inc. 1992, Interactive Data Language, Version 3.0 (Boulder, RSI)
Prusti, T., Adorf, H.-M, & Meurs, E. J. A. 1992, A&A, 261, 685
Ultsch, A. 1993a, in Information and Classification, eds. O. Opitz, B. Lausen, and R. Klar (Berlin, Springer-Verlag), p. 301
Ultsch, A. 1993b, in Information and Classification eds. O. Opitz, B. Lausen, and R. Klar (Berlin, Springer-Verlag), p. 307