



 136 kB PostScript reprint
136 kB PostScript reprint
Next: Automated Globular Cluster
Up: Data Modeling and
Previous: An Approach for
Astronomical Data Analysis Software and Systems IV
ASP Conference Series, Vol. 77, 1995
Book Editors: R. A. Shaw, H. E. Payne, and J. J. E. Hayes
Electronic Editor: H. E. Payne
A. Llebaria, P. Lamy, P. Malburet
Laboratoire d'Astronomie Spatiale du CNRS, BP 8, F-13376 Marseille
Cedex 12
Abstract:
A new method for the discrimination of point-like objects in astronomical
images is presented. The method makes use of the surface curvature of the
image, without any a priori knowledge of the shape of the point-like
objects.
The accurate detection and subsequent removal of point-like objects in
astronomical images is a frequent problem. We mention, as examples,
the case of stars pervading an extended objects, or cosmic ray impacts on
CCD images. The problem is often complicated by various distortions affecting
the point-like objects, such as, saturation, variable Point Spread Function (PSF)
in the field-of-view, and irregular images which preclude the use of fitting
methods. We propose a new approach
to the problem based on the properties of surface curvature which is related
to peaks, pits and flats in images and therefore contain the key information
to discriminate point-like objects.
The intensity of an image can be viewed
as a two-dimensional surface in a three-dimensional space with the two spatial
coordinates forming two of the three dimensions and the intensity axis forming
the third dimension. Surface curvature will describe how much this surface is
bending in a given direction at a particular point; it involves the first
and second partial derivatives with respect to the spatial coordinates and
thus involves the spatial neighborhood of the point. It is readily
understandable that surface curvature will turn out be a powerful means of
discriminating objects in images.
Practical experiments with the surface curvature of astronomical images
have quickly revealed the superiority of dealing with the log of the
intensity, 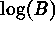 , rather than with the intensity itself. The
justifications of this transformation are easily understood because, (1)
the range of curvatures will be narrower on the
, rather than with the intensity itself. The
justifications of this transformation are easily understood because, (1)
the range of curvatures will be narrower on the 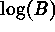 images
than on the intensity images, insuring a better detection of faint objects, and
(2) point-like objects, such as stars may be viewed, at least in a first
approximation, as having a Gaussian shape. The logarithmic transformation
will generate similar paraboloids (i.e., having the same parameters)
for which the maximum of curvature takes place at their tops. Practically,
the logarithmic transformation of the star images will exhibit a coarse
paraboloidal shape which can be easily localized from the maximum of
curvature.
images
than on the intensity images, insuring a better detection of faint objects, and
(2) point-like objects, such as stars may be viewed, at least in a first
approximation, as having a Gaussian shape. The logarithmic transformation
will generate similar paraboloids (i.e., having the same parameters)
for which the maximum of curvature takes place at their tops. Practically,
the logarithmic transformation of the star images will exhibit a coarse
paraboloidal shape which can be easily localized from the maximum of
curvature.
A detailed analysis of surface curvature can be found in Peet and Sahota
(1985). This analysis shows that at each regular point of a surface we can
easily determine 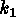 and
and 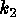 , the local minimum and maximum curvatures,
respectively.
, the local minimum and maximum curvatures,
respectively. 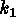 and
and 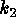 are invariant under rigid motions of the surface.
Two other curvatures are often defined; the Gaussian or total curvature
are invariant under rigid motions of the surface.
Two other curvatures are often defined; the Gaussian or total curvature 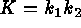 , and the mean curvature
, and the mean curvature 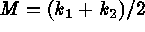 ; but it turns out that the
principal curvatures
; but it turns out that the
principal curvatures 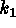 and
and 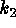 are best suited to the detailed
characterization required by our problem.
are best suited to the detailed
characterization required by our problem.
As curvature is a geometric property of continuous surfaces, we must apply a
continuous model to the discrete array of 2-D data in order to deduce
local derivatives, and from this the local curvatures. Even if more complex models
can be used, a simplified facet model of second order (Halarick 1984), is good
enough when a small set of points is involved in the estimation.
For the 3 3 patch window the practical calculation of
3 patch window the practical calculation of 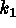 and
and 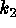 is
extremely simple. The surface
is
extremely simple. The surface 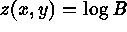 is approximated by a quadric
is approximated by a quadric
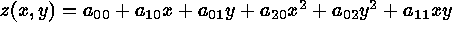 and the coefficients are determined using the least squares fit to the real
surface on a
and the coefficients are determined using the least squares fit to the real
surface on a 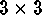 neighborhood of the pixel under consideration.
neighborhood of the pixel under consideration.
It is quite convenient to discuss the surface curvature in the (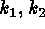 )
space as illustrated in Figure 1. Using the above convention,
)
space as illustrated in Figure 1. Using the above convention, 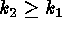 ,
and only the corresponding half plane is therefore allowed. Also, according
to the above definitions, if a curve on the surface is concave up, the
surface curvature in that direction is positive and vice-versa. The allowed
half-plane of Figure 1 (left side) is divided in three regions by the
,
and only the corresponding half plane is therefore allowed. Also, according
to the above definitions, if a curve on the surface is concave up, the
surface curvature in that direction is positive and vice-versa. The allowed
half-plane of Figure 1 (left side) is divided in three regions by the 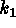 and
and
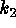 axis. The two axis themselves correspond to parabolic points, with ridges on
the
axis. The two axis themselves correspond to parabolic points, with ridges on
the 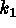 axis (
axis (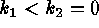 ), and valleys on the
), and valleys on the 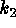 axis (
axis (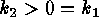 ). The second quadrant
). The second quadrant 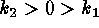 , is the region of the saddle points.
The elliptic points are located in the remaining two half-quadrants,
distinguished by their concavity: pits for
, is the region of the saddle points.
The elliptic points are located in the remaining two half-quadrants,
distinguished by their concavity: pits for 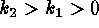 , and peaks for
, and peaks for 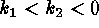 . Obviously, a plane is at the origin
. Obviously, a plane is at the origin 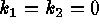 .
.
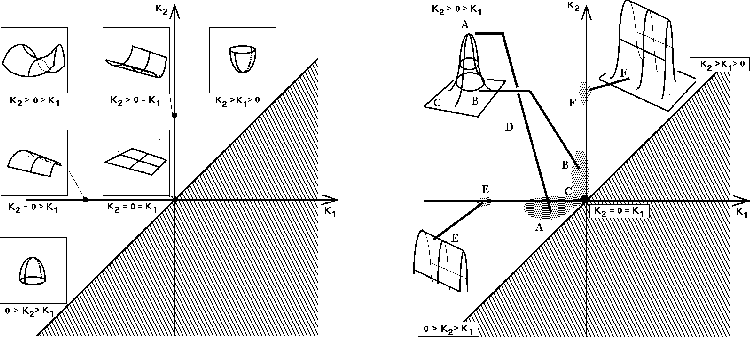
Figure:
(Left side).Surface curvature visualized in the plane of the two principal
curvatures  and
and  .
(Right side).A practical
.
(Right side).A practical  ,
, 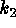 diagram for an astronomical image. The
regions of interest are related to specific parts or curvatures of real
objects.
Original PostScript figure (53 kB)
diagram for an astronomical image. The
regions of interest are related to specific parts or curvatures of real
objects.
Original PostScript figure (53 kB)
Let us now consider how the above theoretical considerations apply to real
astronomical images. Figure 1 (right side) is a sketch of the (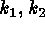 )
diagram based on a CCD image which exhibits an extended source; the tail of
comet P/Halley, a rich star field, and various defects and artifacts. The
features of this (
)
diagram based on a CCD image which exhibits an extended source; the tail of
comet P/Halley, a rich star field, and various defects and artifacts. The
features of this (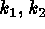 ) diagram are sufficiently general to localize the
various domains of interest and to establish the appropriate criteria for the
discrimination.
) diagram are sufficiently general to localize the
various domains of interest and to establish the appropriate criteria for the
discrimination.
The main feature of the diagram is a ``butterfly''
pattern composed of two wings A and B and a central core C. Both wings
pertain to stars, wing A to their top portions and wing B to their bottom
portions. These latter parts are fairly asymmetric saddle
points leaning to valleys, and explain the closeness of the wing B to
the 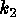 axis. In fact, the orientation of the wing, as given for instance
by the slope
axis. In fact, the orientation of the wing, as given for instance
by the slope 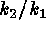 of their symmetry axis, is a very good estimate of
the anisotropy of the surface curvature. For instance, elongated
(trailed) star images will induce a rotation of wing A. The central core C
obviously correspond to the flat part of the image; essentially the
extended object and the background. Finally, two additional features are
conspicuous in the diagram, the blobs E and F respectively localized on
the
of their symmetry axis, is a very good estimate of
the anisotropy of the surface curvature. For instance, elongated
(trailed) star images will induce a rotation of wing A. The central core C
obviously correspond to the flat part of the image; essentially the
extended object and the background. Finally, two additional features are
conspicuous in the diagram, the blobs E and F respectively localized on
the 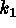 and
and 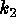 axis. They correspond to elongated structures in the
original image which involve both ridges (top parts) and valleys (bottom
parts). These structures are typically bad columns in the CCD and saturated
star images which spill off along the column direction.
axis. They correspond to elongated structures in the
original image which involve both ridges (top parts) and valleys (bottom
parts). These structures are typically bad columns in the CCD and saturated
star images which spill off along the column direction.
It is now a very simple matter to establish criteria for discriminating objects
in the original image. These criteria are written in terms on conditions on
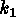 and
and 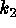 or on a combination of the two. From the initial image we
define a mask (a binary image) defining the subset of
pixels in the original image which belongs to the ``flat'' regions. The
complementary subset includes all invalid points from stars, saturations, etc.
or on a combination of the two. From the initial image we
define a mask (a binary image) defining the subset of
pixels in the original image which belongs to the ``flat'' regions. The
complementary subset includes all invalid points from stars, saturations, etc.
The purpose of the next and final phase is to replace patches of invalid
pixels in the original intensity image by a local interpolation, the so-called
pyramidal interpolation, using a non-linear multiresolution method which
resembles the
Haar wavelet analysis and synthesis.
The procedure starts by shrinking the original 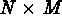 pixels image to a
pixels image to a
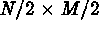 image. Each pixel in the latter corresponds to an area
of
image. Each pixel in the latter corresponds to an area
of 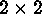 pixels in the former. Their value is a mean of valid pixels
in the
pixels in the former. Their value is a mean of valid pixels
in the 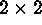 related area. If 3 or 4 pixels in this area are invalid,
the mean is classed as invalid. After this first pass, we obtain an
image of means and a corresponding binary image or mask of valid or invalid
means. Repeating this procedure builds another series of images
(means and mask) of lower resolution. The image of means is called the analysis
image.
related area. If 3 or 4 pixels in this area are invalid,
the mean is classed as invalid. After this first pass, we obtain an
image of means and a corresponding binary image or mask of valid or invalid
means. Repeating this procedure builds another series of images
(means and mask) of lower resolution. The image of means is called the analysis
image.
The procedure is repeated l times until either the extinction of patches of
invalid pixels is obtained, or 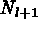 or
or 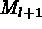 are too small
(that is equal to or
less than 4 pixels on a side). If some final pixels are invalid, they are
replaced by values estimated from a global adjustment of a quadratic surface
over the remaining valid pixels. After this, all pixels are valid at
the lowest resolution level and the synthesis process can start.
are too small
(that is equal to or
less than 4 pixels on a side). If some final pixels are invalid, they are
replaced by values estimated from a global adjustment of a quadratic surface
over the remaining valid pixels. After this, all pixels are valid at
the lowest resolution level and the synthesis process can start.
The synthesis is done by (1) expanding the synthesis image built in the
previous l-1st step by 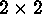 , (2) substitute invalid pixels in the
analysis image at this step l with the corresponding pixels from the above
expanded image, and take this image (with substituted pixels) as the new
synthesis image at this step.
The procedure stops when the initial resolution is recovered. The method
reconstitutes, in each patch of invalid pixels, the low resolution estimate
achieved with valid pixel neighbors.
, (2) substitute invalid pixels in the
analysis image at this step l with the corresponding pixels from the above
expanded image, and take this image (with substituted pixels) as the new
synthesis image at this step.
The procedure stops when the initial resolution is recovered. The method
reconstitutes, in each patch of invalid pixels, the low resolution estimate
achieved with valid pixel neighbors.
This procedure needs a minimal percentage of valid pixels (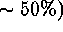 to
obtain significant results. When the number of valid pixels is very low,
the threshold to obtain a significant mean from a
to
obtain significant results. When the number of valid pixels is very low,
the threshold to obtain a significant mean from a 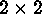 area in the
analysis step can be reduced to one valid pixel.
area in the
analysis step can be reduced to one valid pixel.
We have presented a new method for the discrimination of point-like objects
using surface curvature. The characterization by the curvature offers a
very general and flexible method which can be adapted to any specific problem
without any necessary a priori knowledge of the shape of the point-like
objects. A few trials are basically what is needed to determine the threshold
for discrimination. Another potential application is the removal of cosmic
rays events from single exposure CCD images (when the exposure has been
duplicated, the preferred approach is obviously the comparison of the two
images). These impact events appear as very sharp peaks which may be unambiguously
discriminated by their curvature.
References:
Lamy, P. L., Pederson, H., & Vio, R., 1987, A&A, 187, 661
Peet, F. G., & Sahorta, T. S. 1985, IEEE Trans. Pattern Anal.
Machine Intelligence, Vol. PAMI-7, 734
Halarick 1984, IEEE Trans. Pattern Anal. Machine Intelligence,
Vol. PAMI-6, 58




 136 kB PostScript reprint
136 kB PostScript reprint
Next: Automated Globular Cluster
Up: Data Modeling and
Previous: An Approach for
adass4_editors@stsci.edu
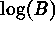 , rather than with the intensity itself. The
justifications of this transformation are easily understood because, (1)
the range of curvatures will be narrower on the
, rather than with the intensity itself. The
justifications of this transformation are easily understood because, (1)
the range of curvatures will be narrower on the 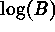 images
than on the intensity images, insuring a better detection of faint objects, and
(2) point-like objects, such as stars may be viewed, at least in a first
approximation, as having a Gaussian shape. The logarithmic transformation
will generate similar paraboloids (i.e., having the same parameters)
for which the maximum of curvature takes place at their tops. Practically,
the logarithmic transformation of the star images will exhibit a coarse
paraboloidal shape which can be easily localized from the maximum of
curvature.
images
than on the intensity images, insuring a better detection of faint objects, and
(2) point-like objects, such as stars may be viewed, at least in a first
approximation, as having a Gaussian shape. The logarithmic transformation
will generate similar paraboloids (i.e., having the same parameters)
for which the maximum of curvature takes place at their tops. Practically,
the logarithmic transformation of the star images will exhibit a coarse
paraboloidal shape which can be easily localized from the maximum of
curvature.
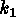 and
and 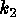 , the local minimum and maximum curvatures,
respectively.
, the local minimum and maximum curvatures,
respectively. 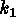 and
and 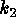 are invariant under rigid motions of the surface.
Two other curvatures are often defined; the Gaussian or total curvature
are invariant under rigid motions of the surface.
Two other curvatures are often defined; the Gaussian or total curvature 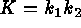 , and the mean curvature
, and the mean curvature 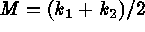 ; but it turns out that the
principal curvatures
; but it turns out that the
principal curvatures 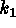 and
and 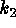 are best suited to the detailed
characterization required by our problem.
are best suited to the detailed
characterization required by our problem.
 3 patch window the practical calculation of
3 patch window the practical calculation of 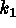 and
and 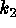 is
extremely simple. The surface
is
extremely simple. The surface 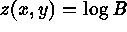 is approximated by a quadric
is approximated by a quadric
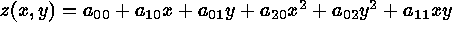 and the coefficients are determined using the least squares fit to the real
surface on a
and the coefficients are determined using the least squares fit to the real
surface on a 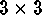 neighborhood of the pixel under consideration.
neighborhood of the pixel under consideration.
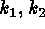 )
space as illustrated in Figure 1. Using the above convention,
)
space as illustrated in Figure 1. Using the above convention, 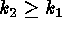 ,
and only the corresponding half plane is therefore allowed. Also, according
to the above definitions, if a curve on the surface is concave up, the
surface curvature in that direction is positive and vice-versa. The allowed
half-plane of Figure 1 (left side) is divided in three regions by the
,
and only the corresponding half plane is therefore allowed. Also, according
to the above definitions, if a curve on the surface is concave up, the
surface curvature in that direction is positive and vice-versa. The allowed
half-plane of Figure 1 (left side) is divided in three regions by the 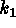 and
and
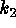 axis. The two axis themselves correspond to parabolic points, with ridges on
the
axis. The two axis themselves correspond to parabolic points, with ridges on
the 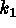 axis (
axis (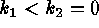 ), and valleys on the
), and valleys on the 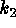 axis (
axis (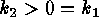 ). The second quadrant
). The second quadrant 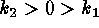 , is the region of the saddle points.
The elliptic points are located in the remaining two half-quadrants,
distinguished by their concavity: pits for
, is the region of the saddle points.
The elliptic points are located in the remaining two half-quadrants,
distinguished by their concavity: pits for 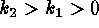 , and peaks for
, and peaks for 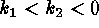 . Obviously, a plane is at the origin
. Obviously, a plane is at the origin 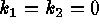 .
.

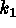 and
and 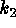 .
(Right side).A practical
.
(Right side).A practical 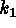 ,
, 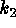 diagram for an astronomical image. The
regions of interest are related to specific parts or curvatures of real
objects.
diagram for an astronomical image. The
regions of interest are related to specific parts or curvatures of real
objects.
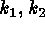 )
diagram based on a CCD image which exhibits an extended source; the tail of
comet P/Halley, a rich star field, and various defects and artifacts. The
features of this (
)
diagram based on a CCD image which exhibits an extended source; the tail of
comet P/Halley, a rich star field, and various defects and artifacts. The
features of this (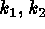 ) diagram are sufficiently general to localize the
various domains of interest and to establish the appropriate criteria for the
discrimination.
) diagram are sufficiently general to localize the
various domains of interest and to establish the appropriate criteria for the
discrimination.
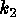 axis. In fact, the orientation of the wing, as given for instance
by the slope
axis. In fact, the orientation of the wing, as given for instance
by the slope 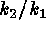 of their symmetry axis, is a very good estimate of
the anisotropy of the surface curvature. For instance, elongated
(trailed) star images will induce a rotation of wing A. The central core C
obviously correspond to the flat part of the image; essentially the
extended object and the background. Finally, two additional features are
conspicuous in the diagram, the blobs E and F respectively localized on
the
of their symmetry axis, is a very good estimate of
the anisotropy of the surface curvature. For instance, elongated
(trailed) star images will induce a rotation of wing A. The central core C
obviously correspond to the flat part of the image; essentially the
extended object and the background. Finally, two additional features are
conspicuous in the diagram, the blobs E and F respectively localized on
the 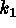 and
and 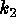 axis. They correspond to elongated structures in the
original image which involve both ridges (top parts) and valleys (bottom
parts). These structures are typically bad columns in the CCD and saturated
star images which spill off along the column direction.
axis. They correspond to elongated structures in the
original image which involve both ridges (top parts) and valleys (bottom
parts). These structures are typically bad columns in the CCD and saturated
star images which spill off along the column direction.
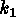 and
and 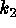 or on a combination of the two. From the initial image we
define a mask (a binary image) defining the subset of
pixels in the original image which belongs to the ``flat'' regions. The
complementary subset includes all invalid points from stars, saturations, etc.
or on a combination of the two. From the initial image we
define a mask (a binary image) defining the subset of
pixels in the original image which belongs to the ``flat'' regions. The
complementary subset includes all invalid points from stars, saturations, etc.
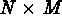 pixels image to a
pixels image to a
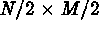 image. Each pixel in the latter corresponds to an area
of
image. Each pixel in the latter corresponds to an area
of 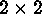 pixels in the former. Their value is a mean of valid pixels
in the
pixels in the former. Their value is a mean of valid pixels
in the 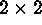 related area. If 3 or 4 pixels in this area are invalid,
the mean is classed as invalid. After this first pass, we obtain an
image of means and a corresponding binary image or mask of valid or invalid
means. Repeating this procedure builds another series of images
(means and mask) of lower resolution. The image of means is called the analysis
image.
related area. If 3 or 4 pixels in this area are invalid,
the mean is classed as invalid. After this first pass, we obtain an
image of means and a corresponding binary image or mask of valid or invalid
means. Repeating this procedure builds another series of images
(means and mask) of lower resolution. The image of means is called the analysis
image.
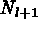 or
or 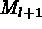 are too small
(that is equal to or
less than 4 pixels on a side). If some final pixels are invalid, they are
replaced by values estimated from a global adjustment of a quadratic surface
over the remaining valid pixels. After this, all pixels are valid at
the lowest resolution level and the synthesis process can start.
are too small
(that is equal to or
less than 4 pixels on a side). If some final pixels are invalid, they are
replaced by values estimated from a global adjustment of a quadratic surface
over the remaining valid pixels. After this, all pixels are valid at
the lowest resolution level and the synthesis process can start.
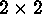 , (2) substitute invalid pixels in the
analysis image at this step l with the corresponding pixels from the above
expanded image, and take this image (with substituted pixels) as the new
synthesis image at this step.
The procedure stops when the initial resolution is recovered. The method
reconstitutes, in each patch of invalid pixels, the low resolution estimate
achieved with valid pixel neighbors.
, (2) substitute invalid pixels in the
analysis image at this step l with the corresponding pixels from the above
expanded image, and take this image (with substituted pixels) as the new
synthesis image at this step.
The procedure stops when the initial resolution is recovered. The method
reconstitutes, in each patch of invalid pixels, the low resolution estimate
achieved with valid pixel neighbors.
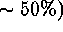 to
obtain significant results. When the number of valid pixels is very low,
the threshold to obtain a significant mean from a
to
obtain significant results. When the number of valid pixels is very low,
the threshold to obtain a significant mean from a 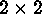 area in the
analysis step can be reduced to one valid pixel.
area in the
analysis step can be reduced to one valid pixel.