



 120 kB PostScript reprint
120 kB PostScript reprint
Next: Interactive Fitting of
Up: Data Modeling and
Previous: Data Modeling and
Astronomical Data Analysis Software and Systems IV
ASP Conference Series, Vol. 77, 1995
Book Editors: R. A. Shaw, H. E. Payne, and J. J. E. Hayes
Electronic Editor: H. E. Payne
G. Hill
Dominion Astrophysical Observatory, Herzberg Institute of Astronomy,
National Research Council of Canada, 5071 West Saanich Road,
Victoria BC V8X 4M6, Canada
Abstract:
In this paper I outline the FORTRAN programs available at
the DAO to process and synthesize spectra, loosely
described under the generic name REDUCE. The viewpoint is that
of a research scientist who develops and uses his own software, and who
writes collaboratively for colleagues. Much of the software has been
available on the DAO's VAX machines since the early 80s and is slowly
being converted to SUNs, although recent developments involve the use of
DEC Alphas. The rationale behind the various reduction and analytic
software is outlined, as well as the way the programs are
controlled, e.g., menu, questions and answers, keywords and values, or
the cursor. Some particularly useful tools are mentioned,
such as, interpolation, optimization, and error analysis.
Since the mid-70s, I have been developing software for the reduction of
digital spectra. Initially, the software
was developed to process digitized scans
of photographic spectra to measure radial velocities (RV)
using techniques akin to those employed by Grant measuring engines, or
the DAO equivalent: ARCTURUS. This involved line-by-line measurements
( VELMEAS, Hill et al. 1982a), which was inadequate when
blended profiles were encountered. Considering that binary stars
were the major source of data, this was not much of an
advance, but it did serve to give me experience with digital data
and interactive graphics. When the IUE satellite flew, I spent a
lot of time writing software to plot the data, and, later,
to measure the lines by fitting Gaussian, Lorentzian, or rotational
profiles to the data--- sans reseau marks. This software, now called
VLINE (Hill et al. 1982b), was combined with REDUCE
(Hill et al. 1982c) to provide the basis for the next development.
The need to measure blended line strengths spurred me
(reluctantly) to modify REDUCE to include scans of the
calibration wedges, in order to convert density to intensity. This led
to the re-discovery of the ``Baker density'' (Baker 1925; de Vaucouleurs
1968), which provides a reliable way to generate intensity from the
characteristic curve.
Early in the 80s, McLean (1981a,b) wrote a cross-correlation
package for the velocity analysis of binary stars, and used data from
the DAO to demonstrate the method. He applied it to the most difficult
of systems---the W UMa stars---and showed that good velocities could
result from the method. This was a breakthrough, and really marked the
advent of ``modern'' binary-star velocity measurements. In 1981 I wrote
software ( VCROSS) (Hill 1982a) that also used the
technique, following a visit from McLean's advisor, Ron Hilditch. It is
now the heart of most of the velocity measures that I make.
As the software began to be developed I started exporting it, and
continue to do so. Its use was originally on a collaborative basis but
I have now abandoned that. But initial development of
any new software is still on a collaborative basis.
In this paper I outline the software I have been responsible for
developing at the DAO. A previous summary is given by Hill & Fisher
(1986a). Note that throughout the paper, program names are given in
bold face.
In this section it is worth describing the data. The
software was originally written for high dispersion spectroscopy, i.e.,
plates that were 8 in long taken, at 2.5--6.5Åmm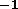 ,
and (under-)sampled every 7--8micron. Later, the software
was modified to handle low dispersion spectra---(80Åmm
,
and (under-)sampled every 7--8micron. Later, the software
was modified to handle low dispersion spectra---(80Åmm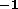 ).
Both of these extremes produced problems: the
former because the size of the data sets (typically 25,000 by 4)
was too small by a factor of 3--4.
and the latter because of the difficulty in automatically predicting the
position of an arc line in a crowded spectrum accurately enough for it
to be measured automatically. The latter problem was harder to solve.
The storage problem required the switch to the VAX.
In the mid-1980s, when the Reticon became available, it was easy to convert
the software to deal with it, particularly when the detector was
linear.
).
Both of these extremes produced problems: the
former because the size of the data sets (typically 25,000 by 4)
was too small by a factor of 3--4.
and the latter because of the difficulty in automatically predicting the
position of an arc line in a crowded spectrum accurately enough for it
to be measured automatically. The latter problem was harder to solve.
The storage problem required the switch to the VAX.
In the mid-1980s, when the Reticon became available, it was easy to convert
the software to deal with it, particularly when the detector was
linear.
The thrust of the observing programs has been twofold: (1) to measure
velocities of stars, and (2) to measure the line strengths, or equivalent
widths (EW) of spectral lines. In the former case the measurements are
quite routine for single stars or galaxies, since there are rarely any
complications. A simple fit to the peak of the
cross-correlation-function (CCF) will generally suffice, though
a red-shifted emission-line galaxy spectrum might pose
problems of interpretation. For binary stars the spectra are more
complex, and a successful measurement demands a
composite CCF or a series of spectral lines, depending on what you are
doing. It is an exacting task to extract this information, even with a
high signal-to-noise (S/N) CCF or line profile. The critical
problem is matching line-shapes to the fitted function. When I first
began the measurement of highly blended profiles, typified by W UMa
systems, I fitted Gaussian profiles to the CCFs. They gave good mass
ratios, but the systemic velocities from the two orbits taken
independently almost always differed. Once realistic shapes were used
to measure the CCFs, however, the systemic
velocities became consistent and the precision of the velocity measures
improved. It then became possible to measure masses to the 1--3% accuracy
that one desires for the study of stellar evolution (Andersen 1991). I
refer the reader to some recent papers on V566 Oph (Hill et al. 1989b) and
V599 Aql (Hill & Khalesseh 1991).
These developments drove me
toward more realistic fitting functions, mostly defined by
the data themselves and not, as before, simply chosen by
virtue of being analytic. This approach parallels the
point-spread-function (PSF) concept used in direct imaging. The same
problem is encountered in measuring line profiles. Here the
observations have not been smoothed and added, like that of a CCF, and
S/N is usually a problem. Again, without a realistic profile shape,
an EW measurement may not be very good. The ability to measure
EWs with excellent precision for blended spectra has been enhanced by
the work of Bagnuolo & Geis (1991), who developed a useful algorithm to
separate out the component spectra. The tomographic method they employ
derives from medicine, and has proven most useful, as shown by Hill &
Khalesseh (1993) for V1425 Cyg, Hill & Holmgren (1994) for Y Cyg, and
Hill et al. (1994) for CC Cas. Another method, developed by Simon & Sturm
(1994), promises to be even better.
Another spur to software development was the availability of data with high
S/N (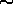 2000:1). Naturally, EW measurements are easier, but such
high quality data need to be matched to stellar
atmosphere models to derive directly the effective temperature (T
2000:1). Naturally, EW measurements are easier, but such
high quality data need to be matched to stellar
atmosphere models to derive directly the effective temperature (T ),
surface gravity (log g), rotational velocity
),
surface gravity (log g), rotational velocity 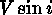 ,
abundance (log Fe/H), and microturbulence (
,
abundance (log Fe/H), and microturbulence (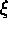 ). To do, this the
Model atmospheres of Kurucz, calculated over a suitable grid (every 500K
from 7500--11,500K, 0.5 dex steps in log g from 3.0--4.5, unequal steps of
0.3--0.5dex in log Fe/H from -1 to +1, and at 0, 1, 2, and 4km
). To do, this the
Model atmospheres of Kurucz, calculated over a suitable grid (every 500K
from 7500--11,500K, 0.5 dex steps in log g from 3.0--4.5, unequal steps of
0.3--0.5dex in log Fe/H from -1 to +1, and at 0, 1, 2, and 4km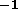 for
for
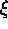 ) are required. The size of this grid, when coupled with a
requirement for spectral coverage of at least 500Å (sampled at
0.01Å), produces some difficulties in memory size. At high dispersion
with the Reticon, we typically sample 1870 points and cover only
70Å. Any analysis would require something larger than that to
enable H
) are required. The size of this grid, when coupled with a
requirement for spectral coverage of at least 500Å (sampled at
0.01Å), produces some difficulties in memory size. At high dispersion
with the Reticon, we typically sample 1870 points and cover only
70Å. Any analysis would require something larger than that to
enable H to be examined. (Note that in an A-star the hydrogen
lines might extend over 100Å and still not
reach the continuum). From these figures, we need about 260MB
of memory to handle just 20Å of spectrum. We are not there yet;
our current need, without including log Fe/H as an unknown, is 50MB.
to be examined. (Note that in an A-star the hydrogen
lines might extend over 100Å and still not
reach the continuum). From these figures, we need about 260MB
of memory to handle just 20Å of spectrum. We are not there yet;
our current need, without including log Fe/H as an unknown, is 50MB.
While the CCD and Reticon have simplified spectroscopy, they have also
produced the potential for inaccuracy, since wavelength
calibrations are made at different times. Unlike a photographic
plate, where all the information needed to analyze it is carried on it
(arcs, star, clear plate and calibration data), the digital detectors
generate sequential files which must be tracked. It is, of
course, a problem for the observer and not one intrinsic to the
detector. With non-coudé systems, arcs should be
taken before and after each stellar exposure. For coudé systems,
where the system is stable, it is not necessary to get arcs with the
In addition we need bias frames (CCD), darks perhaps,
and certainly flat-fields. An echelle observation creates a particular
difficulty, as well as an opportunity, but we do not have such a
spectrograph at the DAO (thank God!). Shortridge's FIGARO software,
however, is particularly effective in processing echelle spectra.
My philosophy has largely been defined by my
experience. As someone who started programming in FORTRAN in the early
1960s I have had many years to develop bad habits as well as to gain a good
knowledge of the language. This, coupled with a structured approach
and excellent software editors, has meant that a new program can be developed
remarkably quickly for each new application. With the
simplifications that came to us from the VAXs acquired throughout the
early 1980s, I discovered that monolithic programs were far too
inefficient. Generalizing problems seemed to get me into more trouble
than it was worth. For that reason I have adopted the philosophy of
writing independent programs to do different tasks. This
philosophy covers graphics, as well as the application itself.
Initially I wrote a ``catch-all'' plotting package, where one or two calls
would define the whole graph, but I quickly abandoned it as being
awkward and unwieldy. Now each application has its own graphics.
This has simplified program
development a great deal, since one does not need a manual to revise the
graphics. Smaller programs are easier to understand and modify.
I have concluded that the software must be interactive, driven by the cursor
and keywords---questions and answers must be minimized. It took a
while before I realized that a system of keywords and associated values,
tasks, etc., would be very useful. I developed my own decoding software to
enable the strings to be interpreted (see Hill & Fisher 1986a,b). It
really made program operation much easier. One could measure a velocity in
about 15 minutes using ARCTURUS, so the computer had to give answers quickly.
The programs must be easy to use, i.e., they all must have the same ``look''
or ``feel.'' With the system of keywords and graphics, with mostly identical
cursor commands, I have largely achieved this goal. All the software has
manuals. But converting from printed (dedicated word-processor) to on-line
manuals has been particularly burdensome.
Many of the repetitive tasks (measuring arcs,
linearization, measuring velocities of single stars) are organized to
work from a file of file names which can be processed in sequence,
either automatically or manually. My favorite automatic feature is the
playback mode, which stems from the robot welding on the Japanese
assembly lines. Hard copy is a factor here since I have always felt it
necessary to be able to retrace the reduction steps, particularly
during the analysis process. For the automatic processing hard copy is
therefore integral to the process.
Graphics have always been a problem. Initially the software was
developed for a Tektronix 4012 terminal (768 by 1024) and its hard-copy
unit. From Tektronix's PLOT 10, higher level graphics routines were
written to facilitate program development ( TGRAPHLIB, Hill
1986). With the growth of laser printers and PostScript, this software
became inadequate, so I converted to Lick Mongo (Allen &
Pogge 1991). This, too, created difficulties in exporting my software
because Lick Mongo is not widely available.
I am currently converting to PGPLOT (Pearson 1989), which is
simpler to implement off-site.
The hardware platform also has an effect on things. The swing from VAXs to
SUNs leaves software developers caught between two stools since one's clients
are not all shifting at once. Thus I have been stuck with trying to maintain
two systems (even the switch from VAXes to Alphas is not routine). Fortunately
some simplifications have occurred along the way: the general adoption of a
single hardware platform, FITS (Wells et al. 1981), and later, the large
software packages IRAF and FIGARO (Shortridge 1987). But for
reductions as specialized and as difficult as found in the binary star
arena, ``canned,'' generalized software cannot do the job.
In this section I deal with all the
steps leading up to measuring a digital spectrum;
analysis will be covered in the next section. Prior to that, the way
that I do book-keeping is noted.
Typically, a datafile name is based on the detector, telescope,
year, and sequence number of the observation. A CCD image (number 1780)
taken with the 1.22 m telescope in 1994 would have a file name
C122941780. In addition to this, I follow the convention defined by
Gulliver (1976) and Irwin (1978); this simple scheme
facilitates
record-keeping since each type of file or each reduction process
simply alters the prefix. The arcs, clear plates, etc., are therefore
uniquely identified with the stellar observations. The exact
processing path depends on whether one has photographic or
CCD (or Reticon) data. For photographic spectroscopy, the data are
produced by a PDS machine which scans both arcs, the stellar spectrum,
and a predetermined stretch of clear plate. The calibration is also
scanned at this time. Such a series of scans yields the
files listed in Table 1. As noted in the table, some of these steps are
omitted for the digital detector.

Table: File-naming convention for plate or file 122941780
The original DAO disk FITS file system was
written by Poeckert in 1981, and has seen many incarnations since then.
Each processing step that a spectrum undergoes is logged in the
header to show what has happened to the data. This, along
with the above file-naming sequence, allows the user to know the status
of their reductions in an instant.
These are routine since the scans all have related names.
In dealing
with Reticon data, we try to emulate the photographic procedure. Given a
long string of observations, the program RET72 allows one to
produce a similar set of files. The data are plotted and examined,
the flats are identified for a given night, and an average defined.
Given the starting and ending file numbers, the data are
normalized by the flats. RET72 automatically identifies
arcs straddling stellar spectra and renames them, prefixing them with
an ``F'' under the name of each stellar spectrum. The result for each
stellar file is an ``F-file''
comprising the straddling files abutted end to end (2 dimensions).
Incidentally, the arcs are automatically identified by a skewness value
 1000, but the algorithm will fail for emission-line spectra.
The whole process can be done manually.
1000, but the algorithm will fail for emission-line spectra.
The whole process can be done manually.
A similar scheme is planned to convert the CCD data that I am now
acquiring at the DAO to one-dimensional (1-D) form. When using data
from the AAT or WHT, I use the FIGARO software to produce the 1-D
files that feed the reduction software. The arcs are measured by
REDUCE (Hill et al. 1982a), an interactive program based on the
method uses to measure arcs with ARCTURUS. The heart of the
scheme is a standard plate---the prediction of a position x in
micron---for a given 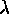 , based on the spectrograph parameters. In
essence, it is a differential method for finding the correction of each
line from a predicted position. One must first
identify one line with a given pixel (hardly an onerous
task); that value is contained in the F-file which RET72
produces. Once a spectrum has been measured, the keystrokes are
recorded and later measures are done in a playback mode. The same arcs,
which might also straddle other stellar observations, are not re-measured
but are updated according to the velocity correction to the sun.
, based on the spectrograph parameters. In
essence, it is a differential method for finding the correction of each
line from a predicted position. One must first
identify one line with a given pixel (hardly an onerous
task); that value is contained in the F-file which RET72
produces. Once a spectrum has been measured, the keystrokes are
recorded and later measures are done in a playback mode. The same arcs,
which might also straddle other stellar observations, are not re-measured
but are updated according to the velocity correction to the sun.
Once the arcs are measured, the spectra are linearized in 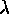 .
The conversion is based on an interpolation using INTEP (Hill
1982b), which uses cubic splines to interpolate a reasonable
curve through the data. It is an extraordinarily effective
workhorse in all the reduction and analysis programs.
.
The conversion is based on an interpolation using INTEP (Hill
1982b), which uses cubic splines to interpolate a reasonable
curve through the data. It is an extraordinarily effective
workhorse in all the reduction and analysis programs.
As noted in Section 2.1 the types of measures we need to make are:
Done either line-by-line, or all together. With binary
stars, the measures may be very difficult;
These are also very difficult, and are
generally only made for single stars;
The measures of line strengths and rotational velocities
are also line-by-line and very difficult. The spectra often have low S/N;
For high dispersion work we
are looking at the physical parameters of single stars, which is a much
easier, but CPU-intensive task. To date we have only worked on high S/N data
(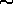 2500:1) and small 20Å stretches of spectrum. The software is
ready to deal with spectra of B--A stars to measure T
2500:1) and small 20Å stretches of spectrum. The software is
ready to deal with spectra of B--A stars to measure T , log
, log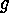 ,
,
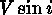 , log Fe/H and
, log Fe/H and 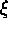 .
.
All of these applications require wavelength linearized spectra,
normalized to the continuum. The format of choice is FITS, although I
occasionally write conversion software to provide the desired FITS
format (the conversion from ASCII already exists). In this section I
outline the programs in regular use at the DAO.
RET72 allows
the user to plot raw data, average the flat field observations,
normalize and assemble files in the desired forms of arc (F-files,
2-D) and stellar (S) files. It produces FITS files that can be
measured for arc, linearized, and then rectified to the continuum
by REDUCE. FIGARO performs the same function when we are
dealing with CCD results from the WHT or AAT. RET72 is routinely
used at the telescope, where it enables the observer to monitor the night's
work very closely. Monitoring has been done off-site from Manitoba.
VLINE measures up to 12 lines
simultaneously. It requires a file of line identifications, and will fit
either Gaussian, Lorentzian, rotational, or digital (PSF) profiles to
selected non-contiguous pieces of the data.
VCROSS measures RV by cross-correlating selected pieces of
spectrum with a reference spectrum or template. The reference spectrum
may be real or synthetic (see Hill et al. 1993). It can fit analytic or
digital profiles to the CCF, produce PSF digital profiles for
use, create artificial binaries for testing, and combine inhomogeneous
(data sampled at different wavelength intervals) FITS files.
The 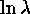 conversion is done automatically. The last
two features are transparent to the user. It can run from a list of file
names interactively or automatically (only
recommended for single stars).
conversion is done automatically. The last
two features are transparent to the user. It can run from a list of file
names interactively or automatically (only
recommended for single stars).
VLINESUM measures RV by summing lines identified from a line list.
It simulates an RV scanner, and is useful for working on visual binaries
where the separations are small, and where the blended profiles will be
further masked by the smoothing effect of a cross-correlation.
VLINE measures up to 12 lines simultaneously, and will fit either
Gaussian, Lorentzian, rotational, or digital (PSF) profiles to selected
non-contiguous pieces of the data yielding EW, FWHM, and 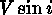 .
LINEMEAS is a less sophisticated version of VLINE, and
only measures single (unblended) lines. It fits various profiles and is
fast to use.
.
LINEMEAS is a less sophisticated version of VLINE, and
only measures single (unblended) lines. It fits various profiles and is
fast to use.
TOMOGRAPHY separates a series of composite spectra into two
components. Given a series of spectra measured for RV (both
components), it will deconvolve them into separate components. When
cross-correlated with a reference spectrum, the resultant CCF provides
the CCF PSF-profiles with which to re-measure the material, and hence to
repeat the process.
Given files of RV and JD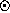 , RVORBIT calculates the
spectroscopic orbit for any combination of parameters. It handles
either single or double-lined spectroscopic binaries using either
Sterne's (1941) method or the method of Lehmann-Filhés (1894).
Errors are calculated by the usual error-matrix analysis and by
Monte-Carlo or bootstrap statistics.
, RVORBIT calculates the
spectroscopic orbit for any combination of parameters. It handles
either single or double-lined spectroscopic binaries using either
Sterne's (1941) method or the method of Lehmann-Filhés (1894).
Errors are calculated by the usual error-matrix analysis and by
Monte-Carlo or bootstrap statistics.
ROTATION generates spectra from large files of synthetic
intensity spectra derived from Kurucz's atmosphere models.
The assembly of
these spectra into a data-base is ongoing.
Models are based on Roche geometry and Collin's (1963) formulation.
Integration is based on the Gauss-Legendre scheme used by Collins and
by Hill (1979) in LIGHT2 . The synthesized spectra are compared
to the observations and then automatically solved for T , log
, log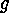 ,
,
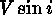 , log Fe/H and
, log Fe/H and 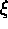 . In certain cases (stars
rotating at
. In certain cases (stars
rotating at 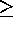 50% of breakup speed, with
50% of breakup speed, with 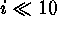 ^o), the
inclination can be determined. It will be become extraordinarily
useful for deriving physical parameters of ``normal'' stars, since it will
happily interpolate automatically in four unknowns.
^o), the
inclination can be determined. It will be become extraordinarily
useful for deriving physical parameters of ``normal'' stars, since it will
happily interpolate automatically in four unknowns.
VSUN calculates the velocity correction to the sun (RV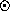 ),
as well as the
heliocentric correction and Julian date. I usually use it to log the
observations as I make them, and certainly use it at the end of the observing
run.
The file it produces, when combined with those generated from earlier
observing, provides the data-base for PHASES (see below).
),
as well as the
heliocentric correction and Julian date. I usually use it to log the
observations as I make them, and certainly use it at the end of the observing
run.
The file it produces, when combined with those generated from earlier
observing, provides the data-base for PHASES (see below).
EPHEMERIS provides planning software for binary star observing.
Given the site, date, UT range needed, and the ephemerides for the
binary stars, the program outputs a table of phases for each night. It
is possible to limit the phases (e.g., ranges around quadrature or
eclipse), and to restrict observations above a given airmass
(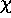 ). It is also possible to pre-select a list of stars with
varying phase constraints. This requires a constraint file of hour angle
(HA) as a function of declination (not the same for all
telescopes, even at the same latitude). The tables can be listed
star-by-star over the nights desired or all stars on
each night. Auxiliary tables giving HA,
). It is also possible to pre-select a list of stars with
varying phase constraints. This requires a constraint file of hour angle
(HA) as a function of declination (not the same for all
telescopes, even at the same latitude). The tables can be listed
star-by-star over the nights desired or all stars on
each night. Auxiliary tables giving HA, 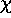 , and RV
, and RV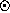 may also
be printed.
may also
be printed.
PHASES calculates the phases from the spectroscopic data-base
produced by VSUN, and sorts and summarizes the data. Histograms
of acquired phase data for each star help in the planning of an
observing run.
Given a file of light-curve data (magnitude vs. phase or
JD) LIGHT2 will solve for any combination of parameters, e.g., relative radii
and polar temperatures of either or both stars, and i. It can also
provide line profiles for W UMa systems for use with VCROSS. It uses
modified black-body intensities and linear limb darkening derived from
theoretical models. It can be modified to use the intensity data
ROTATION uses, once all the atmospheres have been calculated. It
is described by Hill (1979, 1985) and by Hill & Rucinski (1993).
CURFIT is Bevington's (1969) venerable optimizing
program---still remarkably potent. The algorithm has proven to be
wonderfully flexible, and I use it throughout the software described
above. It
has been modified to enable the user to freely vary the parameters.
All non-linear optimizing schemes have their warts
when it comes to local or global minima, but, if used judiciously CURFIT
does the job for these applications. In ROTATION we buttress the
method by doing an extensive search through parameter space to verify
the derived minima. In LIGHT2 I use differing starting points.
CURFIT is used to measure the arc lines in REDUCE and to
perform all of the fitting in VLINE and VCROSS.
INTEP is an interpolation program based on cubic splines
(Tsipouras & Cormier 1973) which has proven to be remarkably useful.
It is stable, and fits a ``reasonable'' curve through data without
the enhanced wiggles one sees in high order polynomials. The software
for this, with some examples, is given by Hill (1982b).
It has proven to be very reliable
for the fitting of continua, unlike
least-squares spline fits which do not go through the data. It is used
for the re-binning of data, e.g.,
in the linearizing process, and within VCROSS when it is used to
homogenize data prior to calculating the CCF.
The calculation of errors is often the bane of
any analysis, particularly when the parameters are correlated. In
spectroscopic orbits, the classic problem involves the derivation of the
longitude of periastron and the time of periastron passage. In
addition CURFIT, as described by Bevington, has a bug in its
error matrix analysis. I find that fits to CCFs often
produce unrealistically low errors, even though the relative values
derived from a list of measures are likely to be accurate. To get
alternative estimates of the errors I have used
Monte-Carlo and bootstrap statistics (e.g., Hill et al. 1989b).
These are easy to
implement---simply take the derived parameters, generate data for each time or
phase, add the observational noise, and solve again. Make
100--1000 solutions, and then calculate the errors in each parameter.
These are equally easy to use, although it becomes impractical
for CPU-bound analyses, such as solving a light curve or using
ROTATION to calculate i for Vega (Gulliver et al. 1994).
It would be interesting to see whether the DEC
Alphas could do the job. The algorithm is straightforward: if you
have n data points, take a random selection of n points from your data
and analyze them. Repeat 100--1000 times, and sort the parameters in
order. The values at the 16-th and 84-th percentile give twice the
error.
Acknowledgments:
I am indebted to my long-time friend and colleagues Drs. Ron Hilditch
and Austin Gulliver for their support and help over the years. Without
this close collaboration the software would never have been written.
References:
Allen, S., & Pogge, R. 1991, Lick Mongo Manual (Santa Cruz,
Univ. of California)
Andersen, J. 1991, A&AR, 3, 91
Baker, A. E. 1925, Proc. RAS Edinburgh, 45, 166
Bevington, P. R. 1969, Data Reduction and Error Analysis
for the Physical Sciences (New York, McGraw-Hill)
Bagnuolo, W. G., & Geis, D. R. 1991, ApJ, 376, 266
Collins, G. W. 1963, ApJ, 138, 1134
de Vaucouleurs, G. 1968, AO, 7, 1513
Gulliver, A. F. 1976, Ph.D. Thesis, University of Toronto
Gulliver, A. F., Hill, G., & Adelman, S. J. 1994, ApJ, 429,
L81
Hill, G. 1979, Publ. Dominion Astrophysical Observatory, 15, 297
Hill, G. 1982a, Publ. Dominion Astrophysical Observatory, 16, 59
Hill, G. 1982b, Publ. Dominion Astrophysical Observatory, 16, 67
Hill, G. 1985, LIGHT2 User Manual
Hill, G. 1986, TGRAPHLIB User Manual (Dominion Astrophysical
Observatory)
Hill, G., Adelman, S. J., & Gulliver, A. F. 1993, PASP,
105, 748
Hill, G., & Fisher, W. A. 1986a, Publ. Dominion Astrophysical
Observatory, 16, 159
Hill, G., & Fisher, W. A. 1986b, The Command System User
Manual, DAO
Hill, G., Fisher, W. A., & Holmgren, D. 1989a, A&A, 211,
81
Hill, G., Fisher, W. A., & Holmgren, D. 1989b, A&A, 218,
152
Hill, G., Hilditch, R. W., Aikman, G. C. L., & Khalesseh,
B. 1994, A&A, 282, 455
Hill, G., & Holmgren, D. 1994, A&A, in press
Hill, G., & Khalesseh, B. 1991, A&A, 245, 517
Hill, G., & Khalesseh, B. 1993, A&A, 276, 57
Hill, G., Ramsden, D., Fisher, W. A., & Morris, S. C.
1982a, Publ. Dominion Astrophysical Observatory 16, 11
Hill, G., & Rucinski, S. M. 1993, in Light Curve Modeling
of Eclipsing Binary Stars, ed. E. F. Milone (New York, Springer-Verlag)
Hill, G., Poeckert, R., & Fisher, W. A. 1982b, Publ. Dominion
Astrophysical Observatory, 16, 27
Hill, G., Poeckert, R., & Fisher, W. A. 1982c, Publ. Dominion
Astrophysical Observatory, 16, 43
Irwin, A. 1978, Ph.D. Thesis, University of Toronto
Lehmann-Filhés, R. 1894, AN, 136, 17
McLean, B. J. 1981a, Ph.D. Thesis, University of St
Andrews.
McLean, B. J. 1981b, MNRAS 195, 931
Pearson, T. J. 1989, PGPLOT User Manual (Pasadena,
California Institute of Technology)
Shortridge, K. 1987, FIGARO Users Guide
(Chilton, Rutherford Appleton Laboratory)
Simon, K. P., & Sturm, E. 1994, A&A, 281, 286
Tsipouras, J., & Cormier, R. V. 1973, Airforce Surveys in
Geophysics, No. 272
Wells, D. C., Greisen, E. W., & Harten, R. H. 1981, A&AS,
44, 363




 120 kB PostScript reprint
120 kB PostScript reprint
Next: Interactive Fitting of
Up: Data Modeling and
Previous: Data Modeling and
adass4_editors@stsci.edu
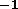 ,
and (under-)sampled every 7--8micron. Later, the software
was modified to handle low dispersion spectra---(80Åmm
,
and (under-)sampled every 7--8micron. Later, the software
was modified to handle low dispersion spectra---(80Åmm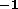 ).
Both of these extremes produced problems: the
former because the size of the data sets (typically 25,000 by 4)
was too small by a factor of 3--4.
and the latter because of the difficulty in automatically predicting the
position of an arc line in a crowded spectrum accurately enough for it
to be measured automatically. The latter problem was harder to solve.
The storage problem required the switch to the VAX.
In the mid-1980s, when the Reticon became available, it was easy to convert
the software to deal with it, particularly when the detector was
linear.
).
Both of these extremes produced problems: the
former because the size of the data sets (typically 25,000 by 4)
was too small by a factor of 3--4.
and the latter because of the difficulty in automatically predicting the
position of an arc line in a crowded spectrum accurately enough for it
to be measured automatically. The latter problem was harder to solve.
The storage problem required the switch to the VAX.
In the mid-1980s, when the Reticon became available, it was easy to convert
the software to deal with it, particularly when the detector was
linear.
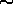 2000:1). Naturally, EW measurements are easier, but such
high quality data need to be matched to stellar
atmosphere models to derive directly the effective temperature (T
2000:1). Naturally, EW measurements are easier, but such
high quality data need to be matched to stellar
atmosphere models to derive directly the effective temperature (T ),
surface gravity (log g), rotational velocity
),
surface gravity (log g), rotational velocity 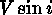 ,
abundance (log Fe/H), and microturbulence (
,
abundance (log Fe/H), and microturbulence (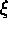 ). To do, this the
Model atmospheres of Kurucz, calculated over a suitable grid (every 500K
from 7500--11,500K, 0.5 dex steps in log g from 3.0--4.5, unequal steps of
0.3--0.5dex in log Fe/H from -1 to +1, and at 0, 1, 2, and 4km
). To do, this the
Model atmospheres of Kurucz, calculated over a suitable grid (every 500K
from 7500--11,500K, 0.5 dex steps in log g from 3.0--4.5, unequal steps of
0.3--0.5dex in log Fe/H from -1 to +1, and at 0, 1, 2, and 4km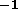 for
for
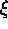 ) are required. The size of this grid, when coupled with a
requirement for spectral coverage of at least 500Å (sampled at
0.01Å), produces some difficulties in memory size. At high dispersion
with the Reticon, we typically sample 1870 points and cover only
70Å. Any analysis would require something larger than that to
enable H
) are required. The size of this grid, when coupled with a
requirement for spectral coverage of at least 500Å (sampled at
0.01Å), produces some difficulties in memory size. At high dispersion
with the Reticon, we typically sample 1870 points and cover only
70Å. Any analysis would require something larger than that to
enable H to be examined. (Note that in an A-star the hydrogen
lines might extend over 100Å and still not
reach the continuum). From these figures, we need about 260MB
of memory to handle just 20Å of spectrum. We are not there yet;
our current need, without including log Fe/H as an unknown, is 50MB.
to be examined. (Note that in an A-star the hydrogen
lines might extend over 100Å and still not
reach the continuum). From these figures, we need about 260MB
of memory to handle just 20Å of spectrum. We are not there yet;
our current need, without including log Fe/H as an unknown, is 50MB.

 1000, but the algorithm will fail for emission-line spectra.
The whole process can be done manually.
1000, but the algorithm will fail for emission-line spectra.
The whole process can be done manually.
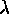 , based on the spectrograph parameters. In
essence, it is a differential method for finding the correction of each
line from a predicted position. One must first
identify one line with a given pixel (hardly an onerous
task); that value is contained in the F-file which RET72
produces. Once a spectrum has been measured, the keystrokes are
recorded and later measures are done in a playback mode. The same arcs,
which might also straddle other stellar observations, are not re-measured
but are updated according to the velocity correction to the sun.
, based on the spectrograph parameters. In
essence, it is a differential method for finding the correction of each
line from a predicted position. One must first
identify one line with a given pixel (hardly an onerous
task); that value is contained in the F-file which RET72
produces. Once a spectrum has been measured, the keystrokes are
recorded and later measures are done in a playback mode. The same arcs,
which might also straddle other stellar observations, are not re-measured
but are updated according to the velocity correction to the sun.
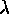 .
The conversion is based on an interpolation using INTEP (Hill
1982b), which uses cubic splines to interpolate a reasonable
curve through the data. It is an extraordinarily effective
workhorse in all the reduction and analysis programs.
.
The conversion is based on an interpolation using INTEP (Hill
1982b), which uses cubic splines to interpolate a reasonable
curve through the data. It is an extraordinarily effective
workhorse in all the reduction and analysis programs.
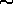 2500:1) and small 20Å stretches of spectrum. The software is
ready to deal with spectra of B--A stars to measure T
2500:1) and small 20Å stretches of spectrum. The software is
ready to deal with spectra of B--A stars to measure T , log
, log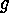 ,
,
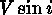 , log Fe/H and
, log Fe/H and 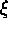 .
.
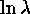 conversion is done automatically. The last
two features are transparent to the user. It can run from a list of file
names interactively or automatically (only
recommended for single stars).
conversion is done automatically. The last
two features are transparent to the user. It can run from a list of file
names interactively or automatically (only
recommended for single stars).
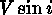 .
LINEMEAS is a less sophisticated version of VLINE, and
only measures single (unblended) lines. It fits various profiles and is
fast to use.
.
LINEMEAS is a less sophisticated version of VLINE, and
only measures single (unblended) lines. It fits various profiles and is
fast to use.
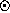 , RVORBIT calculates the
spectroscopic orbit for any combination of parameters. It handles
either single or double-lined spectroscopic binaries using either
Sterne's (1941) method or the method of Lehmann-Filhés (1894).
Errors are calculated by the usual error-matrix analysis and by
Monte-Carlo or bootstrap statistics.
, RVORBIT calculates the
spectroscopic orbit for any combination of parameters. It handles
either single or double-lined spectroscopic binaries using either
Sterne's (1941) method or the method of Lehmann-Filhés (1894).
Errors are calculated by the usual error-matrix analysis and by
Monte-Carlo or bootstrap statistics.
 , log
, log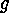 ,
,
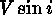 , log Fe/H and
, log Fe/H and 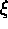 . In certain cases (stars
rotating at
. In certain cases (stars
rotating at 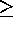 50% of breakup speed, with
50% of breakup speed, with 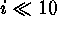 ^o), the
inclination can be determined. It will be become extraordinarily
useful for deriving physical parameters of ``normal'' stars, since it will
happily interpolate automatically in four unknowns.
^o), the
inclination can be determined. It will be become extraordinarily
useful for deriving physical parameters of ``normal'' stars, since it will
happily interpolate automatically in four unknowns.
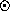 ),
as well as the
heliocentric correction and Julian date. I usually use it to log the
observations as I make them, and certainly use it at the end of the observing
run.
The file it produces, when combined with those generated from earlier
observing, provides the data-base for PHASES (see below).
),
as well as the
heliocentric correction and Julian date. I usually use it to log the
observations as I make them, and certainly use it at the end of the observing
run.
The file it produces, when combined with those generated from earlier
observing, provides the data-base for PHASES (see below).
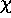 ). It is also possible to pre-select a list of stars with
varying phase constraints. This requires a constraint file of hour angle
(HA) as a function of declination (not the same for all
telescopes, even at the same latitude). The tables can be listed
star-by-star over the nights desired or all stars on
each night. Auxiliary tables giving HA,
). It is also possible to pre-select a list of stars with
varying phase constraints. This requires a constraint file of hour angle
(HA) as a function of declination (not the same for all
telescopes, even at the same latitude). The tables can be listed
star-by-star over the nights desired or all stars on
each night. Auxiliary tables giving HA, 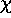 , and RV
, and RV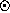 may also
be printed.
may also
be printed.