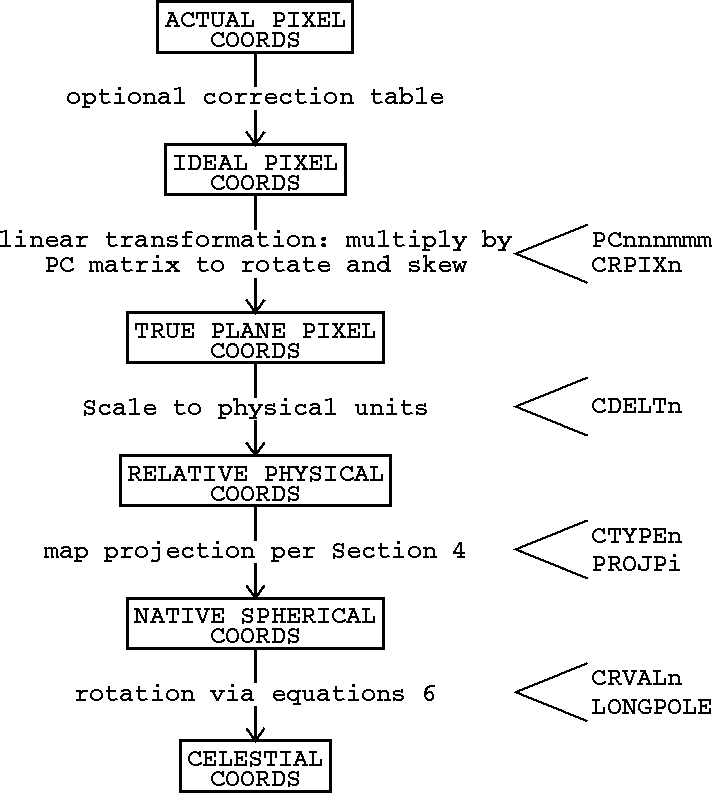
Figure: Conversion of pixel to celestial spherical coordinates Original PostScript figure (3 kB)
E. W. Greisen
National Radio Astronomy Observatory
M. Calabretta
Australia Telescope National Facility
The initial paper describing the Flexible Image Transport System, or FITS format, (Wells, Greisen, & Harten 1981) proposed keywords to describe the physical coordinates of the image. They were CRPIX n for the reference pixel location on pixel axis n, CRVAL n for the coordinate value at that pixel, CDELT n for the increment at that pixel in the coordinate value, and CTYPE n for the type of coordinate. Coordinate rotation---of an unspecified nature---was allowed, and a few possible values for CTYPE n were proposed. The original authors chose to defer discussion of the technical details of coordinate specification until the basic FITS format was accepted generally and until a deeper understanding of image coordinate specification and computation could be obtained.
The time for that discussion is now. While participating in the development of the AIPS software package of the National Radio Astronomy Observatory, Greisen (1983) developed FITS-like syntax and semantics to define both velocity and celestial coordinates. The latter have been widely used for interchanging imagery from a number of instruments at widely differing spectral domains and are fundamental to the present proposal. Greisen defined the reference pixel for celestial coordinates to be the tangent point of the projection. He specified that the first four characters of CTYPE n should be used to give the type of celestial coordinate while the next four characters specified the type of projection (e.g., DEC--TAN). Greisen (1983) gave the mathematics for four projections: orthographic ( SIN), gnomic ( TAN), zenithal equidistant ( ARC), and a special coordinate used by East-West radio interferometers ( NCP). In a second paper, Greisen (1986) added specifications for the stereographic ( STG), sinusoidal ( GLS), Hammer-Aitoff ( AIT), and Mercator ( MER) projections. The current proposal (Greisen and Calabretta, 1994) extends these earlier, widely tested proposals to clarify the logical process by which celestial coordinates are computed, and to specify a very wide range of possible projections. In addition, the current proposal specifies a method to define skew, offset rotations, and even rotations of axes of different physical type into each other. It also specifies a method to describe the units of the coordinates and to provide a second coordinate description for an axis.

Figure: Conversion of pixel to celestial spherical coordinates
Original PostScript figure (3 kB)
In the current proposal, we regard the conversion from simple pixel
counts to a full coordinate description as a multi-step process
containing one optional and four required steps. These steps are
indicated conceptually in Figure ![]() . The first and
optional step is used to correct the actual image pixel numbers into
those which would have been recorded by an ideal instrument. The
corrections in this ``pixel regularization table'' are expected to be
rather small, so that they may be ignored except in high precision
computations. In the second step, for all types of coordinates, the
vector of reference pixels is subtracted from the vector of pixel
numbers and the result multiplied by a pixel conversion ( PC
iiijjj) matrix to convert from pixel numbers to offsets from the
reference pixel along physical axes but still in pixel units. The
third step is a multiplication by a diagonal matrix ( CDELT
i) to convert to relative coordinate in physical units.
. The first and
optional step is used to correct the actual image pixel numbers into
those which would have been recorded by an ideal instrument. The
corrections in this ``pixel regularization table'' are expected to be
rather small, so that they may be ignored except in high precision
computations. In the second step, for all types of coordinates, the
vector of reference pixels is subtracted from the vector of pixel
numbers and the result multiplied by a pixel conversion ( PC
iiijjj) matrix to convert from pixel numbers to offsets from the
reference pixel along physical axes but still in pixel units. The
third step is a multiplication by a diagonal matrix ( CDELT
i) to convert to relative coordinate in physical units.
The fourth step in the process of finding the true coordinates depends
on the type of axis given in CTYPE n. For simple linear
axes, the true coordinate is found by adding the offset found above to
the reference pixel value given by CRVAL n. Otherwise,
some function of the offset(s), the CRVAL n, and, perhaps,
other parameters must be established by convention and agreement. For
celestial coordinates, the proposed fourth step involves converting
the linear offsets into longitudes and latitudes in the ``native
coordinate system'' for the specified type of projection. These are
rotated, in the fifth step, by the usual spherical formulæ to
longitudes and latitudes in the desired standard coordinates (e.g.,
Equatorial, Galactic, etc.) The native coordinate
system is, for azimuthal and conical projections, one which has its
north pole at the reference pixel. For cylindrical and conventional
projections, the native coordinate system has its origin at the
reference pixel. The rotation from native to standard coordinates is
illustrated in Figure ![]() . The keyword LONGPOLE is
proposed to specify the native longitude of the north pole of the
standard system. The default value for LONGPOLE is to be 180
degrees to support current usage. Extra keywords PROJP j
are defined to provide additional parametric information needed by
some of the projections.
. The keyword LONGPOLE is
proposed to specify the native longitude of the north pole of the
standard system. The default value for LONGPOLE is to be 180
degrees to support current usage. Extra keywords PROJP j
are defined to provide additional parametric information needed by
some of the projections.
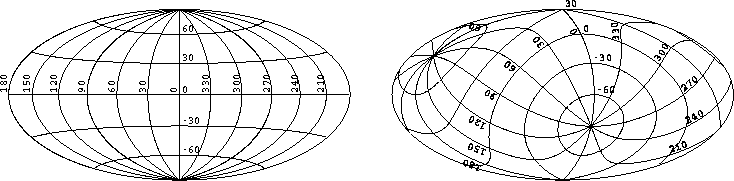
Figure: Conversion of native (left) to standard (right) spherical
coordinates for the Hammer-Aitoff projection.
Original PostScript figure (6 kB)
The original FITS paper (Wells, Greisen, & Harten 1981) naively assumed that the units along each axis could be implied simply by the contents of the CTYPE n keyword and that they would be in the basic SI units. Outside of celestial coordinates, both of these assumptions have apparently failed in practice. Therefore we propose that a new character-valued keyword CUNIT n be added to describe the units used for coordinates on axis n. For celestial angular coordinates, following the proposed projection conventions, these units will be degrees ( 'deg '). Additional discussion and agreements will be needed to determine how one will represent other coordinate types.
In some cases, the axes of an image may be described as having more than one coordinate. An example of this would be the frequency, velocity, and wavelength along a spectral axis (only one of which, of course, could be linear). To allow up to 8 additional descriptions of each axis, we propose the addition of the follow optional, but now reserved, keywords.

where 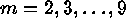 for the second through ninth
alternate axis coordinate and
for the second through ninth
alternate axis coordinate and 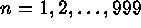 for axis 1
through 999.
for axis 1
through 999.
To improve the use of these coordinates for astrometric purposes, three new keywords are proposed. EQUINOX replaces EPOCH for the epoch of the mean equator and equinox in years. MJD-OBS gives the modified Julian date of observation in days and RADECSYS gives the frame of reference of equatorial coordinates as FK4, FK4-NO-E, FK5, GAPPT.
Greisen, E. W. 1986, AIPS Memo No. 46 (Charlottesville, National Radio Astronomy Observatory)
Greisen E. W., Calabretta, M. 1994, in preparation
Wells, D. C., Greisen, E. W., & Harten, R. H. 1981, A&AS, 44, 363