



 6200 kB PostScript reprint
6200 kB PostScript reprint
Next: Distributed Software for
Up: Network Information Systems
Previous: Network Information Systems
Astronomical Data Analysis Software and Systems IV
ASP Conference Series, Vol. 77, 1995
Book Editors: R. A. Shaw, H. E. Payne, and J. J. E. Hayes
Electronic Editor: H. E. Payne
N. Brummell and J. Toomre
Joint Institute for Laboratory Astrophysics, Department of
Astrophysical, Planetary and Atmospheric Sciences, University of Colorado,
Boulder, CO 80309-0440
Abstract:
Numerical simulations of highly turbulent flows in astrophysics benefit
greatly from recent advances in high performance computing. Yet such
three-dimensional modelling raises major problems in
capturing, moving, and analyzing the resulting massive data sets necessary
to sample the evolving intricate dynamics. Thus archiving, networking, and
visualization are as essential as the actual act of computing when it comes
to real scientific progress.
An interdisciplinary team of researchers at several institutions
(Universities of Colorado, Chicago, and Minnesota, Michigan State University,
and National Center for Atmospheric Research) is working jointly on problems in
geophysical and astrophysical fluid dynamics (GAFD) to utilize
massively-parallel architectures to increase the spatial resolution in
three-dimensional simulations of GAFD turbulence. Within our ``grand
challenge'' team efforts, we are employing variously pseudo-spectral,
finite-difference, multi-grid, and piecewise-parabolic method (PPM)
approaches in studying the intense turbulence encountered in both planetary
and stellar settings. The scale of these simulations requires
corresponding progress in the computational sciences, both in order to
develop and optimize software for massively-parallel computers and to
capture and visualize the resulting massive data sets.
Our research related to astrophysics has so far concentrated largely on
turbulent compressible convection within stars. In particular, the
vigorous turbulence that results from convective instability within
rotating stars not only serves to transport heat but also to redistribute
angular momentum and chemical species, and can yield magnetic dynamo
action. A hallmark of such turbulence constrained by rotation and
stratification is that large-scale coherent structures and strong mean
flows can coexist with the intense smaller-scale turbulence. Our work
with three-dimensional direct simulations of turbulent compressible
convection influenced by rotation is motivated by trying to understand how
stars and giant planets rotate differentially, and in particular to examine
the redistribution of angular momentum that leads to differential rotation
within a star like the sun. As one example, these studies seek to resolve
a major challenge raised recently by helioseismology, wherein acoustic
oscillations of the sun are used to probe the structure and dynamics of the
solar convection zone. Preliminary results from helioseismology (cf. Gough
& Toomre 1991) suggest that the sun is rotating differentially with depth
and latitude in a manner very different from predictions based on earlier
numerical simulations. Those spherical shell simulations of rotating
anelastic convection (e.g., Gilman & Miller 1986; Glatzmaier 1987) dealt
with effectively laminar convective flows, whereas our recent work suggests
that fully turbulent compressible flows appear to yield very
different transport properties for angular momentum. This holds out the
hope that in due course simulations of GAFD turbulence carried out in
appropriate spherical geometries and with the inclusion of adequate stellar
physics (realistic equations of state and opacities, ionization effects)
may help to resolve the basic dynamical puzzle now being raised by
helioseismology. However, understanding such nonlinear dynamics at a
fundamental level raises formidable challenges because of the broad range
of physical scales that must be resolved. High-performance computing
offers the opportunity to make substantial inroads for studying the
properties of such astrophysical turbulence.
The basic difficulty with trying to model turbulence in most natural
settings, and certainly so in a stellar convection zone, is that the active
dynamical scales of convection encompass a formidable range.
Turning to the sun, we expect that the largest-scale turbulent flows deep
within the convection zone should possess scales comparable to the overall
depth of that zone (occupying the outer 30 percent by radius, or about
200,000km in depth). Yet the density scale height near the top of the
zone is only about 100km, and one readily observes there intense turbulent
convection in the form of granulation with horizontal scales of order 1,000
km. Detectable there, too, are supergranulation flow patterns with scales of
order 30,000km. However, we can estimate that viscous dissipation is
operating at scales of order 0.1km or smaller, suggesting that the active
dynamical scales of turbulence in such a zone range at least from 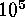 to
to
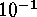 km, or thus over six decades in each physical dimension. The
most intricate three-dimensional turbulence simulations to date have just
begun dealing with order
km, or thus over six decades in each physical dimension. The
most intricate three-dimensional turbulence simulations to date have just
begun dealing with order 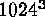 spatial modes, capturing three decades in
each dimension. As we will discuss below, such
spatial modes, capturing three decades in
each dimension. As we will discuss below, such 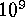 spatial zone
calculations to study the evolution of turbulence for typically
spatial zone
calculations to study the evolution of turbulence for typically 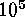 time
steps make rather interesting demands on processors, memory, communications,
and data capture. Though we may have to wait for quite some time before
time
steps make rather interesting demands on processors, memory, communications,
and data capture. Though we may have to wait for quite some time before
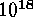 zone simulations become tractable (if ever), we can take some
comfort in realizing that the hints of structured turbulence first realized
with
zone simulations become tractable (if ever), we can take some
comfort in realizing that the hints of structured turbulence first realized
with 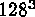 simulations are now seen in fascinating detail with the
simulations are now seen in fascinating detail with the
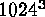 ``hero'' calculations of the day. Another three decades of
resolution (and degrees of freedom) in each physical dimension may
well herald other surprises in the resulting turbulent dynamics. The
optimism of theoretical physics encourages great extrapolations to be made,
and in that spirit we hope that the turbulence calculations of
``hero'' calculations of the day. Another three decades of
resolution (and degrees of freedom) in each physical dimension may
well herald other surprises in the resulting turbulent dynamics. The
optimism of theoretical physics encourages great extrapolations to be made,
and in that spirit we hope that the turbulence calculations of
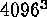 -class likely by the end of this decade and century may provide
substantial clues about the inner workings of a real star like the sun.
Yet we recognize that all such modelling is of the large-eddy simulation
(LES) variety, requiring some manner of sub-grid-scale (SGS) representation
of the unresolved scales.
-class likely by the end of this decade and century may provide
substantial clues about the inner workings of a real star like the sun.
Yet we recognize that all such modelling is of the large-eddy simulation
(LES) variety, requiring some manner of sub-grid-scale (SGS) representation
of the unresolved scales.
The nature of our computational challenges are revealed by considering some
of the attributes of a 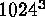 -mode turbulence simulation. For fully
compressible convection, we typically use as working variables the three
components of velocity
-mode turbulence simulation. For fully
compressible convection, we typically use as working variables the three
components of velocity 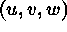 , pressure p, and temperature T.
This implies that the memory requirements are 160 GB, based on
, pressure p, and temperature T.
This implies that the memory requirements are 160 GB, based on 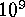 spatial zones
spatial zones  5 variables
5 variables  factor 4 of working space, for
a total of about 20 Gwords. On a 1024-node massively parallel processor
(mpp) system, we effectively need 160MB of memory per node. Turning to
estimates of operation counts for these simulations, the floating point
operation (flop) count per zone per time step range from about 200 for
pseudo-spectral codes to about 4000 for PPM codes. Since the intricate
dynamics needs to be evolved for about 100,000 times steps, the total
operation count for a given simulation are
factor 4 of working space, for
a total of about 20 Gwords. On a 1024-node massively parallel processor
(mpp) system, we effectively need 160MB of memory per node. Turning to
estimates of operation counts for these simulations, the floating point
operation (flop) count per zone per time step range from about 200 for
pseudo-spectral codes to about 4000 for PPM codes. Since the intricate
dynamics needs to be evolved for about 100,000 times steps, the total
operation count for a given simulation are 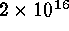 flop using
pseudo-spectral codes and
flop using
pseudo-spectral codes and 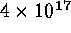 flop using PPM codes. Once a
real Tflops
flop using PPM codes. Once a
real Tflops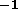 machine (1000 Gflops
machine (1000 Gflops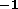 ) is realized, such a pseudo-spectral run
could be accomplished in
) is realized, such a pseudo-spectral run
could be accomplished in 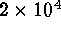 s (about 6 hours), whereas the PPM
run requires
s (about 6 hours), whereas the PPM
run requires 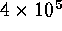 s (about 110 hours). At the sustained 20
Gflops
s (about 110 hours). At the sustained 20
Gflops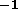 that is about the best performance now, these numbers translate into
that is about the best performance now, these numbers translate into
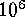 s (280 hours) and
s (280 hours) and 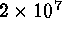 s (5500 hours).
s (5500 hours).
The choice of computational fluid dynamics algorithms to be favored on a
given mpp architecture is considerably influenced by the effective internal
communication speed between processors. The use of fully explicit and
spatially local methods, such as PPM, places the least demands on such
communication. With PPM, our 3--D simulations on regular grids can be
subdivided into many subvolumes, with only values of variables on boundary
zones a few layers deep having to be exchanged after each time step between
processors working on adjacent subvolumes. If the operation count is high,
this is a relatively infrequent event. In contrast, pseudo-spectral codes
assign successive physical planes to the processors, and carry out fast
transforms on these planes within processors, followed by data transposes
when calculations are required in the final dimension. Alternatively, the
transforms may be carried out in parallel across processors, with either
approach requiring fairly intensive data movement. Since the operation
counts with pseudo-spectral codes are typically far more modest than with
PPM, communication currently places major constraints upon the actual
performance realized with the principal mpp contenders.
Of greater concern is how to extract and capture sufficient data to be used
for subsequent visualization and analysis of these intricate turbulent
flows. A single data snapshot of five fields and two tracers at
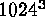 -resolution yields 56GB per dump. If we sample the time evolution
fairly sparsely after every 100 time steps (or
-resolution yields 56GB per dump. If we sample the time evolution
fairly sparsely after every 100 time steps (or 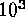 samples per run),
then the full data set is about 56TB per run. Not only is that number
rather large given most current mass storage facilities, but the data flow
rate will also be problematic as the computing machines get faster. On
current 20Gflops
samples per run),
then the full data set is about 56TB per run. Not only is that number
rather large given most current mass storage facilities, but the data flow
rate will also be problematic as the computing machines get faster. On
current 20Gflops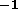 machines, the required data outflow for the PPM code is a
tractable 2.8MBs
machines, the required data outflow for the PPM code is a
tractable 2.8MBs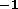 , and for the pseudo-spectral code (with about 20-fold
fewer operations per time step) a more difficult 56MBs
, and for the pseudo-spectral code (with about 20-fold
fewer operations per time step) a more difficult 56MBs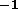 . Present multi-TB
mass stores have sustained transfer rates of 3 to 20MBs
. Present multi-TB
mass stores have sustained transfer rates of 3 to 20MBs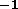 . Data output
from a Tflops
. Data output
from a Tflops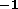 machine would in turn be 0.14GBs
machine would in turn be 0.14GBs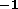 (for PPM) and 2.8GBs
(for PPM) and 2.8GBs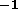 (for pseudo-spectral), or thus at worst a factor
(for pseudo-spectral), or thus at worst a factor 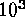 greater than
current mass store rates. Substantial improvements in rates of data output
and capture are anticipated, but it is likely that such data movement
places the severest restraints on efficient simulations of turbulence. The
options to help survive this looming data crunch are to sample full dumps
less often, or to take compressed dumps, or used weighted averages of the
data, or to do smaller problems. More acceptable is to recognize that
investments must be made for data movement and capture that may turn out to
be comparable in cost to that of the mpp itself.
greater than
current mass store rates. Substantial improvements in rates of data output
and capture are anticipated, but it is likely that such data movement
places the severest restraints on efficient simulations of turbulence. The
options to help survive this looming data crunch are to sample full dumps
less often, or to take compressed dumps, or used weighted averages of the
data, or to do smaller problems. More acceptable is to recognize that
investments must be made for data movement and capture that may turn out to
be comparable in cost to that of the mpp itself.

Figure: Perspective full domain view of vertical velocity at one instant
in time in 3-D turbulent convection simulation (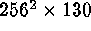 ). Here
). Here
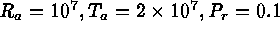 , with the rotating f-plane
domain at latitude
, with the rotating f-plane
domain at latitude 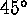 . The rendering has upward-flowing, hot
fluid as bright, with downward-flowing, cold fluid as darker tones. Note
the curvaceous network at the upper surface and the smaller-scale
turbulence at the bottom.
Original PostScript figure (1496 kB)
. The rendering has upward-flowing, hot
fluid as bright, with downward-flowing, cold fluid as darker tones. Note
the curvaceous network at the upper surface and the smaller-scale
turbulence at the bottom.
Original PostScript figure (1496 kB)
Our goals have been to first study the dynamics of increasingly turbulent
states in simplified ``local area'' geometries with the influence of rotation
incorporated via f--plane modelling, and then to proceed toward a more
physical ``global'' geometry encompassing an entire rotating spherical shell
of fluid. Our local-area models consist of a planar layer of fluid
positioned tangentially to a rotating sphere at a latitude 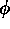 . The
model configuration for the fully compressible treatments is essentially
that of Cattaneo et al. (1991). The physics of the model is simplified by
employing a perfect gas, and fluid properties such as the specific heats,
shear viscosity, and thermal conductivity are also assumed constant. The
flow is confined between two horizontal, impenetrable, stress-free
boundaries, and the fields are assumed to be periodic in the horizontal.
The upper boundary is held at a given temperature, whereas the heat flux is
prescribed on the lower boundary. We then proceed to solve as an initial
value problem the partial differential equations for the conservation of
mass, momentum, and energy, along with the equation of state. The
simulations are characterized by several nondimensional parameters: the
Prandtl number
. The
model configuration for the fully compressible treatments is essentially
that of Cattaneo et al. (1991). The physics of the model is simplified by
employing a perfect gas, and fluid properties such as the specific heats,
shear viscosity, and thermal conductivity are also assumed constant. The
flow is confined between two horizontal, impenetrable, stress-free
boundaries, and the fields are assumed to be periodic in the horizontal.
The upper boundary is held at a given temperature, whereas the heat flux is
prescribed on the lower boundary. We then proceed to solve as an initial
value problem the partial differential equations for the conservation of
mass, momentum, and energy, along with the equation of state. The
simulations are characterized by several nondimensional parameters: the
Prandtl number 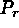 , the ratio of viscosity to thermal conductivity, the
Taylor number
, the ratio of viscosity to thermal conductivity, the
Taylor number 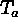 , the ratio of Coriolis to diffusive terms, the Rayleigh
number
, the ratio of Coriolis to diffusive terms, the Rayleigh
number 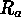 , the ratio of buoyancy forcing to viscous and thermal
dissipation, and the Rossby number
, the ratio of buoyancy forcing to viscous and thermal
dissipation, and the Rossby number 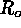 , the ratio of nonlinear advective
to Coriolis forces.
, the ratio of nonlinear advective
to Coriolis forces.
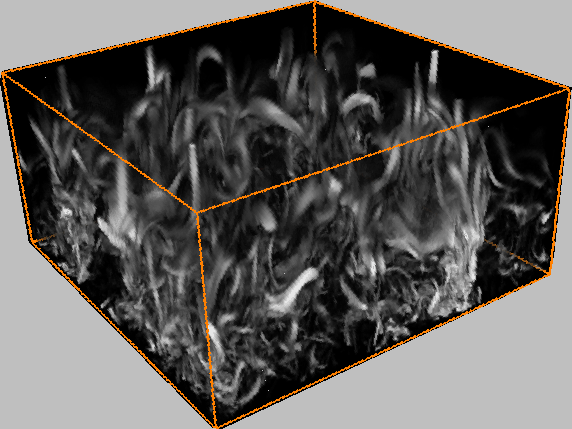
Figure: Perspective 3--D view of enstrophy (vorticity squared) at one
instant in time as a companion to Figure 1. High enstrophy is bright and
opaque whereas low enstrophy is dark and translucent. Distinctive
enstrophy structures are present, with evolving cellular flows near the top
of the layer yielding sheets and tubes of vorticity, whereas in the intense
turbulence at greater depths the vorticity is often organized into
randomly aligned tubes. Large coherent tube-like structures intermingle
with small-scale random vortex tubing in the interior.
Original PostScript figure (1136 kB)
Our main computations shown here involve the solution of the fully
compressible equations using a hybrid finite-difference and pseudo-spectral
code. The vertical structure is treated by fourth-order finite differences
in the interior. The horizontal components are treated by a pseudo-spectral
method that calculates all linear operations and derivatives in spectral
space 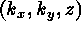 and performs the nonlinear multiplications in
configuration space
and performs the nonlinear multiplications in
configuration space 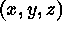 , with the transform between spaces achieved
by fast transform methods. The time discretization is based on an explicit
two-level Adams-Bashforth scheme, and the thermal conduction terms are
treated implicitly with a Crank-Nicholson method.
, with the transform between spaces achieved
by fast transform methods. The time discretization is based on an explicit
two-level Adams-Bashforth scheme, and the thermal conduction terms are
treated implicitly with a Crank-Nicholson method.
We have studied the basic features of fully-developed rotating compressible
turbulence, with special regard to the types of flow structures,
topologies, mean-flow generation, and energy balances that may be achieved.
The simulations typically involve a density contrast across the layer of
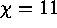 , spanning roughly 5 pressure scale heights. Other parameters
fixed are the ratio of the specific heats,
, spanning roughly 5 pressure scale heights. Other parameters
fixed are the ratio of the specific heats, 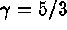 , and the aspect
ratio of the box, at
, and the aspect
ratio of the box, at 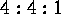 . A series of runs has been made sparsely
populating the four-dimensional parameter space (
. A series of runs has been made sparsely
populating the four-dimensional parameter space (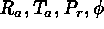 ) of
the model but revealing a rich set of results. We will briefly sample some
of the characteristics of such turbulent convection.
) of
the model but revealing a rich set of results. We will briefly sample some
of the characteristics of such turbulent convection.
Let us first comment on the effects of rotation on the structure and topology
of the turbulent convective flows. We find that convective flows in the
upper thermal boundary layer consist of a nearly laminar, cellular network,
atop a fully turbulent interior, punctuated by vertically-coherent
structures emanating from the upper surface (e.g., Brummell, Hurlburt,
& Toomre 1993, 1995a,b). There is pronounced asymmetry between the strong,
narrow downdrafts and the weak, broad upflows. This is evident in Figure 1,
which shows the local-area computational domain with the vertical velocity
on the visible surfaces shaded according to its strength (see also Figure
5). A plane close to the lower surface of the domain has been removed to
show clearly the difference in scales between the fully-developed
turbulence there and the laminar upper surface. The smoothness of the
upflow regions near the surface is achieved by rapid horizontal expansion
of the ascending fluid elements which will tend to smooth out any
small-scale fluctuations. The cell packing near the top is irregular, and
cells are born and obliterated in an intricate time-dependent fashion. The
Coriolis forces of rotation have changed the characteristics of both the
surface network and the turbulent interior from that of earlier nonrotating
models (Cattaneo et al. 1991). The surface network has become more
curvaceous, less connected and more time-dependent with the addition of
rotational constraints. These changes are due to inertial oscillations of
surface flows induced by the underlying rotation which mobilizes the
network, and to the enhancement of a mechanism for cell destruction and
creation by the background pool of vorticity. In the latter, vorticity
concentrated at the interstices of the downflow network lanes is amplified
by the rotational influence to produce vortices which are strong enough to
evacuate their interiors, thus causing a reversal of the vertical flow and
the eventual destabilization of the vortex itself. These ``spinners'' break
apart the network at the junctions and allow new upflowing cells to form
there.
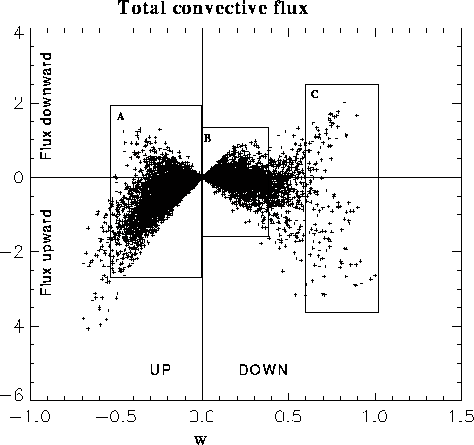
Figure: Phase diagram of pointwise convective flux 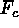 as function of
the vertical velocity in a horizontal plane near midlayer for turbulent
convection with
as function of
the vertical velocity in a horizontal plane near midlayer for turbulent
convection with 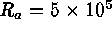 ,
, 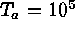 and
and 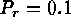 , with
, with
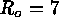 . The boxes A, B and C delineate horizontal sites of upflow,
downflow, and strong downflow within the horizontal sampling plane.
Original PostScript figure (1670 kB)
. The boxes A, B and C delineate horizontal sites of upflow,
downflow, and strong downflow within the horizontal sampling plane.
Original PostScript figure (1670 kB)
We find that the nature of the flows in the turbulent interior are subtly
altered by rotation. The Coriolis forces provide a linear mechanism for
coupling the vertical and horizontal motions, and thus with rotation the
isotropy of energy and enstrophy is enhanced. This manifests itself as the
concentration of vorticity into distinctive tube-like structures with a
very random orientation in the interior of the flow. These vortex tubes
are illustrated in Figure 2, which displays the enstrophy (vorticity squared)
field in a volume rendering. Near the surface, the laminar cellular flow
is dominated by vortex tubes where the coherent downflows form, and by
weaker sheets of vorticity generated by the downflow lanes. At greater
depths, the small-scale turbulence is characterized by intricately
interwoven small intense vortex tubes. Larger structures with vertical
coherence are always in existence, and their presence in conjunction with
Coriolis effects can lead to enhanced Reynolds stresses and thus a
generation of mean flows (cf. Brummell, Xie, Toomre, & Baillie 1995). The
vortex interactions of the small-scale turbulent tubes and the
larger-scale vertically-coherent strong downflowing structures provide a
horizontal mixing mechanism which retards the vertical mixing by the
convection, yielding a mean thermal stratification in the vertical which is
substantially nonadiabatic over much of the interior. This has the
important and surprising consequence that with rotation, buoyancy driving
of such turbulence will be experienced throughout the layer depth, and not
just dominantly in the thermal boundary layers near the top and bottom of
the layer.
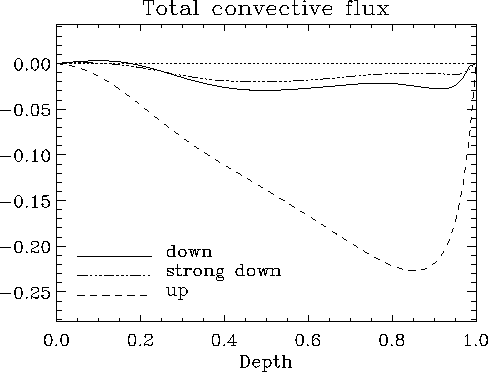
Figure: Horizontally-averaged convective flux 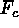 as function of depth
for the case sampled in Figure 3, revealing that the near cancellation of
enthalpy and kinetic fluxes within the downflows leads to the upflows
dominantly carrying the convective flux.
Original PostScript figure (25 kB)
as function of depth
for the case sampled in Figure 3, revealing that the near cancellation of
enthalpy and kinetic fluxes within the downflows leads to the upflows
dominantly carrying the convective flux.
Original PostScript figure (25 kB)

Figure: Vertical velocity w (left) and convective flux 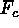 (right)
shown in three horizontal slices near the upper surface, middle and lower
surface in single snapshot of vigorous turbulent convection for
(right)
shown in three horizontal slices near the upper surface, middle and lower
surface in single snapshot of vigorous turbulent convection for 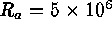 ,
,  ,
, 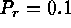 , and
, and 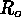 = 2.24. Upflows are
lighter tones, downflows are darker tones. The change from smooth, nearly
laminar flows at the top to disordered, turbulent flows deeper down is
clearly evident. For
= 2.24. Upflows are
lighter tones, downflows are darker tones. The change from smooth, nearly
laminar flows at the top to disordered, turbulent flows deeper down is
clearly evident. For 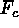 , regions of upflow are blanked out with neutral
grey, and downflow regions encoded either as white or black according to
the sense of
, regions of upflow are blanked out with neutral
grey, and downflow regions encoded either as white or black according to
the sense of 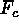 . Figure 4 indicates that horizontal averaging of these
spatially intermittent fluxes in downflows leads to near cancellation.
Original PostScript figure (1908 kB)
. Figure 4 indicates that horizontal averaging of these
spatially intermittent fluxes in downflows leads to near cancellation.
Original PostScript figure (1908 kB)
There is a distinctive transition from laminar to turbulent flows at
greater depths when the Prandtl number 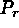 in the simulations was
decreased below a value of about one-third. The flows are vigorously time
dependent and turbulent, yet they exhibit coherent flow patterns
recognizable over several scale heights, contrary to the assumptions of
mixing-length approaches. Further, the surface appearance of the
convection, always being cellular and irregular, does not belie whether the
deeper structures are laminar or turbulent. The transition to turbulence
also results in remarkable changes in how the convection transports the
energy. Namely, in the laminar cases the strong downflows serve to both
carry most of the enthalpy flux upward and a significant kinetic energy
flux downward: the upflow sites make only a modest contribution to both
fluxes. However, once there is transition to turbulence at the greater
depths, there is a prominent change in the role of the downflows, in which
the (upward) enthalpy and (downward) kinetic flux contributions now nearly
cancel each other, leaving the disorganized turbulent motions outside of
those coherent structures to effect most of the overall energy transport.
Thus whereas the larger scales control the convective patterns and their
evolution, the transport is left to the smaller turbulent scales. This is
a striking example of how transports achieved by convection can be
radically modified by transitions to turbulence. Further, there are major
fluctuations in the total convective flux (sum of enthalpy and kinetic
fluxes) from site to site across any given horizontal plane, as the phase
diagram of vertical velocity w and convective flux
in the simulations was
decreased below a value of about one-third. The flows are vigorously time
dependent and turbulent, yet they exhibit coherent flow patterns
recognizable over several scale heights, contrary to the assumptions of
mixing-length approaches. Further, the surface appearance of the
convection, always being cellular and irregular, does not belie whether the
deeper structures are laminar or turbulent. The transition to turbulence
also results in remarkable changes in how the convection transports the
energy. Namely, in the laminar cases the strong downflows serve to both
carry most of the enthalpy flux upward and a significant kinetic energy
flux downward: the upflow sites make only a modest contribution to both
fluxes. However, once there is transition to turbulence at the greater
depths, there is a prominent change in the role of the downflows, in which
the (upward) enthalpy and (downward) kinetic flux contributions now nearly
cancel each other, leaving the disorganized turbulent motions outside of
those coherent structures to effect most of the overall energy transport.
Thus whereas the larger scales control the convective patterns and their
evolution, the transport is left to the smaller turbulent scales. This is
a striking example of how transports achieved by convection can be
radically modified by transitions to turbulence. Further, there are major
fluctuations in the total convective flux (sum of enthalpy and kinetic
fluxes) from site to site across any given horizontal plane, as the phase
diagram of vertical velocity w and convective flux 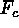 in Figure 3
reveals. In the upflows (A), the pointwise
in Figure 3
reveals. In the upflows (A), the pointwise 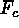 values are sufficiently
skewed that there is a net upward flux (negative) when averaged over all
points, whereas the distribution is more nearly symmetrical for the
moderate downflows (B) and so too for the strong downflows (C), with only a
small value for the net transport emerging after averaging. This is indeed
seen in Figure 4 of the horizontally-averaged
values are sufficiently
skewed that there is a net upward flux (negative) when averaged over all
points, whereas the distribution is more nearly symmetrical for the
moderate downflows (B) and so too for the strong downflows (C), with only a
small value for the net transport emerging after averaging. This is indeed
seen in Figure 4 of the horizontally-averaged 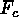 with depth as
contributed in turn by the upflows and the moderate and strong downflow
regions. The contributions from the upflows dominate in the convective
transport.
with depth as
contributed in turn by the upflows and the moderate and strong downflow
regions. The contributions from the upflows dominate in the convective
transport.
The results shown in Figure 4 are extraordinary, implying that throughout
the turbulent layer nearly all the convective flux is carried by the
upflowing material and not the downflows, despite the fact that the
downflows are much more coherent in space and time compared to the random
fluctuations of the smaller scale upflows. The near-zero horizontal
average value in the downflow at any depth is due to a cancellation of the
two components of the convective flux, i.e., the enthalpy flux and the
kinetic flux. Cattaneo et al. (1991) proposed a theory as to why that
might be, suggesting that cancellation of the constituent fluxes at each
point in the downflows is due to a Bernoulli-like balance achieved in the
dynamics, provided that the motion is nearly steady, the mean
stratification is nearly adiabatic, and viscous and thermal conduction are
negligible. These conditions are reasonably well met in the turbulent
simulations. Figure 5, however, points out that this theory may be overly
simplistic. Shown is the vertical velocity and measures of the convective
flux 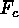 for three depths at a typical time in the simulation. The
convective flux is shown only in the downflows (the upflows are obscured
with a grey mask) with black marking regions of positive convective flux
and white marking regions of negative flux. This rendering reveals that
the cancellation is neither pointwise nor even local. If it conformed to
the theory, then the whole downflow regions would be colored neutrally
gray, or at least would have a very high frequency speckling between small
black and white values. Instead, we see interleaved patches of black and
white where the values of
for three depths at a typical time in the simulation. The
convective flux is shown only in the downflows (the upflows are obscured
with a grey mask) with black marking regions of positive convective flux
and white marking regions of negative flux. This rendering reveals that
the cancellation is neither pointwise nor even local. If it conformed to
the theory, then the whole downflow regions would be colored neutrally
gray, or at least would have a very high frequency speckling between small
black and white values. Instead, we see interleaved patches of black and
white where the values of 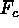 are actually quite large and definitely
non-zero. Surprisingly, however, the horizontal average (i.e., the sum of
all the black and white patches) is nearly zero. The cancellation of the
convective flux appears to be more a phenomenon related to major
intermittency in the flux production, both in time and space, rather than
by pointwise cancellation as was first thought. These are rather subtle
matters, emphasizing that highly turbulent flows can possess transport
properties very different from those of laminar flows.
are actually quite large and definitely
non-zero. Surprisingly, however, the horizontal average (i.e., the sum of
all the black and white patches) is nearly zero. The cancellation of the
convective flux appears to be more a phenomenon related to major
intermittency in the flux production, both in time and space, rather than
by pointwise cancellation as was first thought. These are rather subtle
matters, emphasizing that highly turbulent flows can possess transport
properties very different from those of laminar flows.
This work was supported in part by NSF through grant ECS--9217394
and by NASA through grants NAG5--2218 and NAG5--2256. The simulations were
carried out at the Pittsburgh Supercomputer Center under grant MCA93S005P.
References:
Brummell, N. H., Hurlburt, N. E., & Toomre, J., 1993, in GONG
1992: Seismic Investigation of the Sun and Stars,
ASP Conf. Ser., Vol. 42, ed. T. M. Brown (San Francisco, ASP), p.
61
Brummell, N. H., Hurlburt, N. E., & Toomre, J., 1995a,b, ApJ,
submitted
Brummell, N. H., Xie, X., Toomre, J., & Baillie, C. 1995, in
Proc. GONG'94, Helio- and Asteroseismology,
ASP Conf. Ser.,
ed. R. K. Ulrich (San Francisco, ASP),
in press
Cattaneo, F., Brummell, N. H., Toomre, J., Malagoli, A., &
Hurlburt, N. E. 1991, ApJ, 370, 282
Gilman, P. A., & Miller, J. 1986, ApJ, 61, 585
Glatzmaier, G. A. 1987, in The Internal Solar Angular Velocity,
eds. B. R. Durney & S. Sofia (Dordrecht, Reidel), p. 263
Gough, D. O., & Toomre, J. 1991, ARA&A, 29, 627




 6200 kB PostScript reprint
6200 kB PostScript reprint
Next: Distributed Software for
Up: Network Information Systems
Previous: Network Information Systems
adass4_editors@stsci.edu
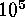 to
to
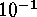 km, or thus over six decades in each physical dimension. The
most intricate three-dimensional turbulence simulations to date have just
begun dealing with order
km, or thus over six decades in each physical dimension. The
most intricate three-dimensional turbulence simulations to date have just
begun dealing with order 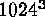 spatial modes, capturing three decades in
each dimension. As we will discuss below, such
spatial modes, capturing three decades in
each dimension. As we will discuss below, such 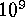 spatial zone
calculations to study the evolution of turbulence for typically
spatial zone
calculations to study the evolution of turbulence for typically 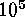 time
steps make rather interesting demands on processors, memory, communications,
and data capture. Though we may have to wait for quite some time before
time
steps make rather interesting demands on processors, memory, communications,
and data capture. Though we may have to wait for quite some time before
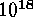 zone simulations become tractable (if ever), we can take some
comfort in realizing that the hints of structured turbulence first realized
with
zone simulations become tractable (if ever), we can take some
comfort in realizing that the hints of structured turbulence first realized
with 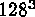 simulations are now seen in fascinating detail with the
simulations are now seen in fascinating detail with the
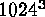 ``hero'' calculations of the day. Another three decades of
resolution (and degrees of freedom) in each physical dimension may
well herald other surprises in the resulting turbulent dynamics. The
optimism of theoretical physics encourages great extrapolations to be made,
and in that spirit we hope that the turbulence calculations of
``hero'' calculations of the day. Another three decades of
resolution (and degrees of freedom) in each physical dimension may
well herald other surprises in the resulting turbulent dynamics. The
optimism of theoretical physics encourages great extrapolations to be made,
and in that spirit we hope that the turbulence calculations of
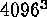 -class likely by the end of this decade and century may provide
substantial clues about the inner workings of a real star like the sun.
Yet we recognize that all such modelling is of the large-eddy simulation
(LES) variety, requiring some manner of sub-grid-scale (SGS) representation
of the unresolved scales.
-class likely by the end of this decade and century may provide
substantial clues about the inner workings of a real star like the sun.
Yet we recognize that all such modelling is of the large-eddy simulation
(LES) variety, requiring some manner of sub-grid-scale (SGS) representation
of the unresolved scales.
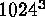 -mode turbulence simulation. For fully
compressible convection, we typically use as working variables the three
components of velocity
-mode turbulence simulation. For fully
compressible convection, we typically use as working variables the three
components of velocity 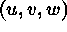 , pressure p, and temperature T.
This implies that the memory requirements are 160 GB, based on
, pressure p, and temperature T.
This implies that the memory requirements are 160 GB, based on 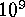 spatial zones
spatial zones  5 variables
5 variables  factor 4 of working space, for
a total of about 20 Gwords. On a 1024-node massively parallel processor
(mpp) system, we effectively need 160MB of memory per node. Turning to
estimates of operation counts for these simulations, the floating point
operation (flop) count per zone per time step range from about 200 for
pseudo-spectral codes to about 4000 for PPM codes. Since the intricate
dynamics needs to be evolved for about 100,000 times steps, the total
operation count for a given simulation are
factor 4 of working space, for
a total of about 20 Gwords. On a 1024-node massively parallel processor
(mpp) system, we effectively need 160MB of memory per node. Turning to
estimates of operation counts for these simulations, the floating point
operation (flop) count per zone per time step range from about 200 for
pseudo-spectral codes to about 4000 for PPM codes. Since the intricate
dynamics needs to be evolved for about 100,000 times steps, the total
operation count for a given simulation are 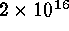 flop using
pseudo-spectral codes and
flop using
pseudo-spectral codes and 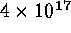 flop using PPM codes. Once a
real Tflops
flop using PPM codes. Once a
real Tflops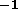 machine (1000 Gflops
machine (1000 Gflops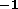 ) is realized, such a pseudo-spectral run
could be accomplished in
) is realized, such a pseudo-spectral run
could be accomplished in 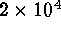 s (about 6 hours), whereas the PPM
run requires
s (about 6 hours), whereas the PPM
run requires 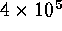 s (about 110 hours). At the sustained 20
Gflops
s (about 110 hours). At the sustained 20
Gflops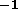 that is about the best performance now, these numbers translate into
that is about the best performance now, these numbers translate into
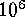 s (280 hours) and
s (280 hours) and 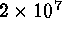 s (5500 hours).
s (5500 hours).
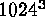 -resolution yields 56GB per dump. If we sample the time evolution
fairly sparsely after every 100 time steps (or
-resolution yields 56GB per dump. If we sample the time evolution
fairly sparsely after every 100 time steps (or 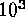 samples per run),
then the full data set is about 56TB per run. Not only is that number
rather large given most current mass storage facilities, but the data flow
rate will also be problematic as the computing machines get faster. On
current 20Gflops
samples per run),
then the full data set is about 56TB per run. Not only is that number
rather large given most current mass storage facilities, but the data flow
rate will also be problematic as the computing machines get faster. On
current 20Gflops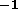 machines, the required data outflow for the PPM code is a
tractable 2.8MBs
machines, the required data outflow for the PPM code is a
tractable 2.8MBs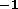 , and for the pseudo-spectral code (with about 20-fold
fewer operations per time step) a more difficult 56MBs
, and for the pseudo-spectral code (with about 20-fold
fewer operations per time step) a more difficult 56MBs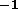 . Present multi-TB
mass stores have sustained transfer rates of 3 to 20MBs
. Present multi-TB
mass stores have sustained transfer rates of 3 to 20MBs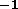 . Data output
from a Tflops
. Data output
from a Tflops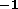 machine would in turn be 0.14GBs
machine would in turn be 0.14GBs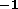 (for PPM) and 2.8GBs
(for PPM) and 2.8GBs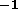 (for pseudo-spectral), or thus at worst a factor
(for pseudo-spectral), or thus at worst a factor 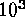 greater than
current mass store rates. Substantial improvements in rates of data output
and capture are anticipated, but it is likely that such data movement
places the severest restraints on efficient simulations of turbulence. The
options to help survive this looming data crunch are to sample full dumps
less often, or to take compressed dumps, or used weighted averages of the
data, or to do smaller problems. More acceptable is to recognize that
investments must be made for data movement and capture that may turn out to
be comparable in cost to that of the mpp itself.
greater than
current mass store rates. Substantial improvements in rates of data output
and capture are anticipated, but it is likely that such data movement
places the severest restraints on efficient simulations of turbulence. The
options to help survive this looming data crunch are to sample full dumps
less often, or to take compressed dumps, or used weighted averages of the
data, or to do smaller problems. More acceptable is to recognize that
investments must be made for data movement and capture that may turn out to
be comparable in cost to that of the mpp itself.

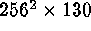 ). Here
). Here
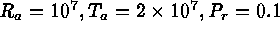 , with the rotating f-plane
domain at latitude
, with the rotating f-plane
domain at latitude 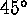 . The rendering has upward-flowing, hot
fluid as bright, with downward-flowing, cold fluid as darker tones. Note
the curvaceous network at the upper surface and the smaller-scale
turbulence at the bottom.
. The rendering has upward-flowing, hot
fluid as bright, with downward-flowing, cold fluid as darker tones. Note
the curvaceous network at the upper surface and the smaller-scale
turbulence at the bottom.
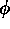 . The
model configuration for the fully compressible treatments is essentially
that of Cattaneo et al. (1991). The physics of the model is simplified by
employing a perfect gas, and fluid properties such as the specific heats,
shear viscosity, and thermal conductivity are also assumed constant. The
flow is confined between two horizontal, impenetrable, stress-free
boundaries, and the fields are assumed to be periodic in the horizontal.
The upper boundary is held at a given temperature, whereas the heat flux is
prescribed on the lower boundary. We then proceed to solve as an initial
value problem the partial differential equations for the conservation of
mass, momentum, and energy, along with the equation of state. The
simulations are characterized by several nondimensional parameters: the
Prandtl number
. The
model configuration for the fully compressible treatments is essentially
that of Cattaneo et al. (1991). The physics of the model is simplified by
employing a perfect gas, and fluid properties such as the specific heats,
shear viscosity, and thermal conductivity are also assumed constant. The
flow is confined between two horizontal, impenetrable, stress-free
boundaries, and the fields are assumed to be periodic in the horizontal.
The upper boundary is held at a given temperature, whereas the heat flux is
prescribed on the lower boundary. We then proceed to solve as an initial
value problem the partial differential equations for the conservation of
mass, momentum, and energy, along with the equation of state. The
simulations are characterized by several nondimensional parameters: the
Prandtl number 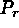 , the ratio of viscosity to thermal conductivity, the
Taylor number
, the ratio of viscosity to thermal conductivity, the
Taylor number 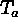 , the ratio of Coriolis to diffusive terms, the Rayleigh
number
, the ratio of Coriolis to diffusive terms, the Rayleigh
number 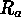 , the ratio of buoyancy forcing to viscous and thermal
dissipation, and the Rossby number
, the ratio of buoyancy forcing to viscous and thermal
dissipation, and the Rossby number 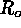 , the ratio of nonlinear advective
to Coriolis forces.
, the ratio of nonlinear advective
to Coriolis forces.

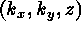 and performs the nonlinear multiplications in
configuration space
and performs the nonlinear multiplications in
configuration space 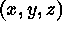 , with the transform between spaces achieved
by fast transform methods. The time discretization is based on an explicit
two-level Adams-Bashforth scheme, and the thermal conduction terms are
treated implicitly with a Crank-Nicholson method.
, with the transform between spaces achieved
by fast transform methods. The time discretization is based on an explicit
two-level Adams-Bashforth scheme, and the thermal conduction terms are
treated implicitly with a Crank-Nicholson method.
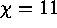 , spanning roughly 5 pressure scale heights. Other parameters
fixed are the ratio of the specific heats,
, spanning roughly 5 pressure scale heights. Other parameters
fixed are the ratio of the specific heats, 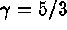 , and the aspect
ratio of the box, at
, and the aspect
ratio of the box, at 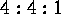 . A series of runs has been made sparsely
populating the four-dimensional parameter space (
. A series of runs has been made sparsely
populating the four-dimensional parameter space (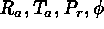 ) of
the model but revealing a rich set of results. We will briefly sample some
of the characteristics of such turbulent convection.
) of
the model but revealing a rich set of results. We will briefly sample some
of the characteristics of such turbulent convection.

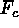 as function of
the vertical velocity in a horizontal plane near midlayer for turbulent
convection with
as function of
the vertical velocity in a horizontal plane near midlayer for turbulent
convection with 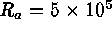 ,
, 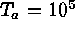 and
and 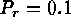 , with
, with
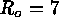 . The boxes A, B and C delineate horizontal sites of upflow,
downflow, and strong downflow within the horizontal sampling plane.
. The boxes A, B and C delineate horizontal sites of upflow,
downflow, and strong downflow within the horizontal sampling plane.

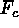 as function of depth
for the case sampled in Figure 3, revealing that the near cancellation of
enthalpy and kinetic fluxes within the downflows leads to the upflows
dominantly carrying the convective flux.
as function of depth
for the case sampled in Figure 3, revealing that the near cancellation of
enthalpy and kinetic fluxes within the downflows leads to the upflows
dominantly carrying the convective flux.

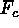 (right)
shown in three horizontal slices near the upper surface, middle and lower
surface in single snapshot of vigorous turbulent convection for
(right)
shown in three horizontal slices near the upper surface, middle and lower
surface in single snapshot of vigorous turbulent convection for 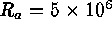 ,
,  ,
, 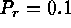 , and
, and 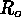 = 2.24. Upflows are
lighter tones, downflows are darker tones. The change from smooth, nearly
laminar flows at the top to disordered, turbulent flows deeper down is
clearly evident. For
= 2.24. Upflows are
lighter tones, downflows are darker tones. The change from smooth, nearly
laminar flows at the top to disordered, turbulent flows deeper down is
clearly evident. For 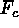 , regions of upflow are blanked out with neutral
grey, and downflow regions encoded either as white or black according to
the sense of
, regions of upflow are blanked out with neutral
grey, and downflow regions encoded either as white or black according to
the sense of 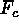 . Figure 4 indicates that horizontal averaging of these
spatially intermittent fluxes in downflows leads to near cancellation.
. Figure 4 indicates that horizontal averaging of these
spatially intermittent fluxes in downflows leads to near cancellation.
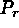 in the simulations was
decreased below a value of about one-third. The flows are vigorously time
dependent and turbulent, yet they exhibit coherent flow patterns
recognizable over several scale heights, contrary to the assumptions of
mixing-length approaches. Further, the surface appearance of the
convection, always being cellular and irregular, does not belie whether the
deeper structures are laminar or turbulent. The transition to turbulence
also results in remarkable changes in how the convection transports the
energy. Namely, in the laminar cases the strong downflows serve to both
carry most of the enthalpy flux upward and a significant kinetic energy
flux downward: the upflow sites make only a modest contribution to both
fluxes. However, once there is transition to turbulence at the greater
depths, there is a prominent change in the role of the downflows, in which
the (upward) enthalpy and (downward) kinetic flux contributions now nearly
cancel each other, leaving the disorganized turbulent motions outside of
those coherent structures to effect most of the overall energy transport.
Thus whereas the larger scales control the convective patterns and their
evolution, the transport is left to the smaller turbulent scales. This is
a striking example of how transports achieved by convection can be
radically modified by transitions to turbulence. Further, there are major
fluctuations in the total convective flux (sum of enthalpy and kinetic
fluxes) from site to site across any given horizontal plane, as the phase
diagram of vertical velocity w and convective flux
in the simulations was
decreased below a value of about one-third. The flows are vigorously time
dependent and turbulent, yet they exhibit coherent flow patterns
recognizable over several scale heights, contrary to the assumptions of
mixing-length approaches. Further, the surface appearance of the
convection, always being cellular and irregular, does not belie whether the
deeper structures are laminar or turbulent. The transition to turbulence
also results in remarkable changes in how the convection transports the
energy. Namely, in the laminar cases the strong downflows serve to both
carry most of the enthalpy flux upward and a significant kinetic energy
flux downward: the upflow sites make only a modest contribution to both
fluxes. However, once there is transition to turbulence at the greater
depths, there is a prominent change in the role of the downflows, in which
the (upward) enthalpy and (downward) kinetic flux contributions now nearly
cancel each other, leaving the disorganized turbulent motions outside of
those coherent structures to effect most of the overall energy transport.
Thus whereas the larger scales control the convective patterns and their
evolution, the transport is left to the smaller turbulent scales. This is
a striking example of how transports achieved by convection can be
radically modified by transitions to turbulence. Further, there are major
fluctuations in the total convective flux (sum of enthalpy and kinetic
fluxes) from site to site across any given horizontal plane, as the phase
diagram of vertical velocity w and convective flux 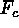 in Figure 3
reveals. In the upflows (A), the pointwise
in Figure 3
reveals. In the upflows (A), the pointwise 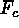 values are sufficiently
skewed that there is a net upward flux (negative) when averaged over all
points, whereas the distribution is more nearly symmetrical for the
moderate downflows (B) and so too for the strong downflows (C), with only a
small value for the net transport emerging after averaging. This is indeed
seen in Figure 4 of the horizontally-averaged
values are sufficiently
skewed that there is a net upward flux (negative) when averaged over all
points, whereas the distribution is more nearly symmetrical for the
moderate downflows (B) and so too for the strong downflows (C), with only a
small value for the net transport emerging after averaging. This is indeed
seen in Figure 4 of the horizontally-averaged 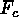 with depth as
contributed in turn by the upflows and the moderate and strong downflow
regions. The contributions from the upflows dominate in the convective
transport.
with depth as
contributed in turn by the upflows and the moderate and strong downflow
regions. The contributions from the upflows dominate in the convective
transport.
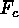 for three depths at a typical time in the simulation. The
convective flux is shown only in the downflows (the upflows are obscured
with a grey mask) with black marking regions of positive convective flux
and white marking regions of negative flux. This rendering reveals that
the cancellation is neither pointwise nor even local. If it conformed to
the theory, then the whole downflow regions would be colored neutrally
gray, or at least would have a very high frequency speckling between small
black and white values. Instead, we see interleaved patches of black and
white where the values of
for three depths at a typical time in the simulation. The
convective flux is shown only in the downflows (the upflows are obscured
with a grey mask) with black marking regions of positive convective flux
and white marking regions of negative flux. This rendering reveals that
the cancellation is neither pointwise nor even local. If it conformed to
the theory, then the whole downflow regions would be colored neutrally
gray, or at least would have a very high frequency speckling between small
black and white values. Instead, we see interleaved patches of black and
white where the values of 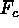 are actually quite large and definitely
non-zero. Surprisingly, however, the horizontal average (i.e., the sum of
all the black and white patches) is nearly zero. The cancellation of the
convective flux appears to be more a phenomenon related to major
intermittency in the flux production, both in time and space, rather than
by pointwise cancellation as was first thought. These are rather subtle
matters, emphasizing that highly turbulent flows can possess transport
properties very different from those of laminar flows.
are actually quite large and definitely
non-zero. Surprisingly, however, the horizontal average (i.e., the sum of
all the black and white patches) is nearly zero. The cancellation of the
convective flux appears to be more a phenomenon related to major
intermittency in the flux production, both in time and space, rather than
by pointwise cancellation as was first thought. These are rather subtle
matters, emphasizing that highly turbulent flows can possess transport
properties very different from those of laminar flows.