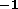 , in the geocentric inertial coordinate system. The observer must
find and extract the appropriate file(s) from the archive and interpolate the
HST state vector data to the relevant times of the observations.
, in the geocentric inertial coordinate system. The observer must
find and extract the appropriate file(s) from the archive and interpolate the
HST state vector data to the relevant times of the observations.
T. B. Ake
Astronomy Programs, Computer Sciences Corporation, Code 681/CSC,
Goddard Space Flight Center, Greenbelt, MD 20771
Many precise measurements with the Hubble Space Telescope ( HST) require knowledge of its position and velocity during the observations. Orbital parallax, velocity aberration, Doppler shift, and light-travel time can all be significant when converting HST observations to the geocentric system, and from there to the barycenter of the solar system. In addition, the quality of observations are affected by the near-earth environment in which HST operates. An observer would be wise to understand such effects as scattered earth light, radiation background, and geomagnetically-induced motion on the data.
One way to determine the motion of HST during an observation is through
the definitive orbit files that are archived at the Space Telescope Science
Institute (ST ScI). Every other day the Flight Dynamics Facility (FDF) at
Goddard Space Flight Center computes the position and velocity of the
HST for the previous two days based on ranging measurements of the
spacecraft. This information is forwarded to the ST ScI in the form of a list
of HST state vectors for each minute of time, with each record giving
the J2000 rectangular components of the position, in km, and velocity, in
kms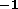 , in the geocentric inertial coordinate system. The observer must
find and extract the appropriate file(s) from the archive and interpolate the
HST state vector data to the relevant times of the observations.
, in the geocentric inertial coordinate system. The observer must
find and extract the appropriate file(s) from the archive and interpolate the
HST state vector data to the relevant times of the observations.
An easier method is to use the onboard ephemeris parameters that are provided with the data sets themselves. When the definitive orbit file is generated by the FDF, a set of ephemeris coefficients is created. The HST flight software uses these coefficients for various spacecraft control functions. During pipeline processing at the ST ScI, these are archived in the *.shh (non-astrometry) or *.dbm (astrometry) header file for each observation. We summarize using this information to compute the position and velocity of the HST.
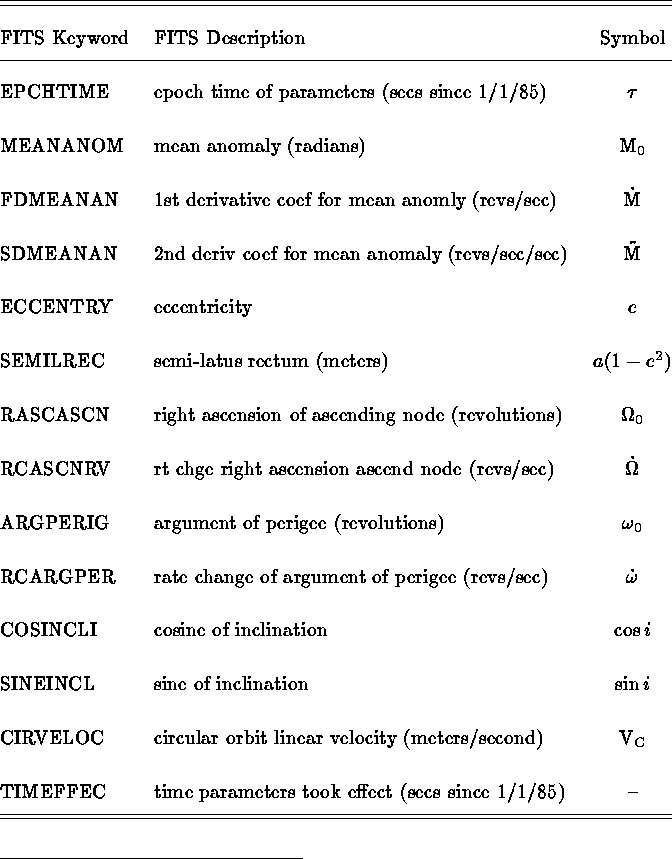
Table: Onboard Ephemeris Model Parameters
The HST travels in a nearly circular orbit, with an altitude of about 600km
and velocity of 7.5kms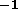 . The orbital model used onboard is based on a
simple two-body system, with perturbations to certain Keplerian elements due to
the proximity of the earth. In Table 1 we list the relevant FITS keywords
and descriptions that can be found in the header files, as well as the symbols
used in the equations below.
. The orbital model used onboard is based on a
simple two-body system, with perturbations to certain Keplerian elements due to
the proximity of the earth. In Table 1 we list the relevant FITS keywords
and descriptions that can be found in the header files, as well as the symbols
used in the equations below.
The steps to compute the geocentric, rectangular coordinates for the HST using the parameters in Table 1 are as follows. First, the observer should verify that the correct onboard ephemeris has been archived with the data. The TIMEFFEC keyword specifies the beginning time at which the parameters are valid and its value should be within 2--3 days before the start of the observations.
For a time of interest, t, calculate the mean anomaly, M, from the initial
position, M , at the epoch time of the parameters,
, at the epoch time of the parameters, 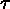 ,
,
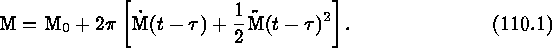
Compute the true anomaly,  , using the equation of center to solve Kepler's
equation. This is typically expressed as a series in
, using the equation of center to solve Kepler's
equation. This is typically expressed as a series in 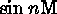 and e.
For small e, terms only up to
and e.
For small e, terms only up to 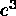 are needed (e.g., Smart 1965, equation V-85),
are needed (e.g., Smart 1965, equation V-85),
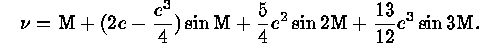
Since trigonometric functions are computationally expensive, HST uses a
different form of this equation involving only 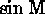 and
and 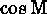 .
Collecting like terms of
.
Collecting like terms of 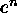 and expanding
and expanding 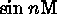 , one can show
, one can show
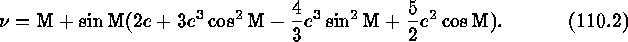
Once the true anomaly is known, then the distance from the center of the earth, r, is
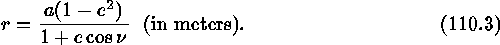
The main perturbation on the orbital elements due to the non-spherical mass
distribution of the earth is the regression of the ascending node,  ,
and the progression of perigee,
,
and the progression of perigee, 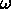 , (Wertz 1978). The instantaneous
values at t are
, (Wertz 1978). The instantaneous
values at t are
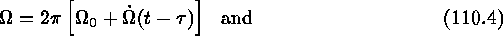

The geocentric HST position, in J2000 rectangular coordinates in meters, is then
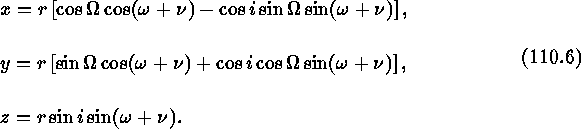
The corresponding equations for radial velocity can be derived by differentiating those for position. Starting with x,
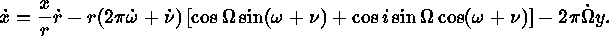
To eliminate the 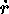 and
and 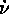 terms, we use a well-known property
of elliptical orbits that the velocity can be represented as the vector sum of
two constant velocities (Smart 1965). These are the velocity,
terms, we use a well-known property
of elliptical orbits that the velocity can be represented as the vector sum of
two constant velocities (Smart 1965). These are the velocity, 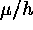 ,
perpendicular to the radius vector and,
,
perpendicular to the radius vector and, 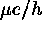 , perpendicular to the
semimajor axis, where
, perpendicular to the
semimajor axis, where 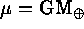 and
and 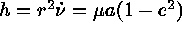 .
Designating V
.
Designating V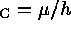 as the circular velocity, we have
as the circular velocity, we have
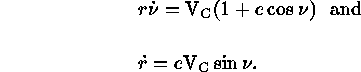
The rectangular velocities can now be determined from the onboard ephemeris parameters. Defining the auxiliary variables
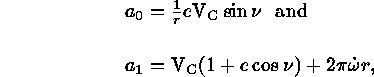
we have
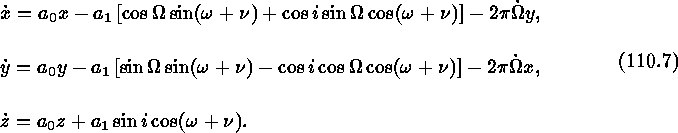
Equations (1)--(7) yield the geocentric state vectors for HST.
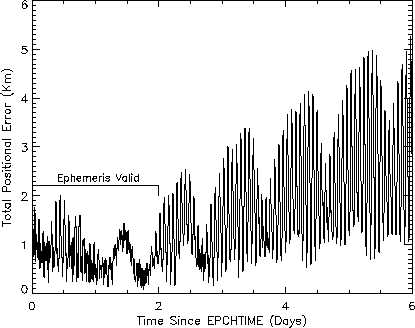
Figure: Typical positional errors from an on-board ephemeris.
Original PostScript figure (82 kB)
We can compare the results from the ephemeris model directly with the
definitive orbit data. In Figure 1 we show the total error in position for
several days during the first week of 1994 April. In this example the error
is below 2km for the two days during which the ephemeris is active. After this
time, the error slowly increases, reaching about 5km a week outside the
two-day range of the model. The error in velocity was found to be only
0.01kms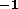 over the whole period investigated. Comparisons for other weeks
indicates that the positional error can be as high as 4km, but the velocity
error is always very small, since the orbit is nearly circular.
over the whole period investigated. Comparisons for other weeks
indicates that the positional error can be as high as 4km, but the velocity
error is always very small, since the orbit is nearly circular.
Results using the onboard ephemeris are accurate enough for most needs. A
positional error of 4km translates to an uncertainty of 1mas at 5.5AU from
the earth, so parallax errors are small for all but nearby passing asteroids
and comets. The geographic position of HST can be determined to
better than 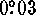 , much more accurately than needed to compute effects due
to the orbital environment. The error in velocity is much smaller than can be
measured with the HST instruments. We conclude that using the onboard
ephemeris eliminates the need to import definitive orbit data. This
exemplifies the value of providing users with self-documenting data sets so
that further analyses can be performed without resorting to additional outside
information.
, much more accurately than needed to compute effects due
to the orbital environment. The error in velocity is much smaller than can be
measured with the HST instruments. We conclude that using the onboard
ephemeris eliminates the need to import definitive orbit data. This
exemplifies the value of providing users with self-documenting data sets so
that further analyses can be performed without resorting to additional outside
information.
Wertz, J. R. 1978, in Spacecraft Attitude Determination and Control (Dordrecht, Reidel), p. 65