This paper describes our GAMMS (Gravitational Adaptive Mesh Multigrid Solver) code, which is a numerical gravitational solver, based upon a multigrid (MG) algorithm and a local refining mesh strategy (AMR, Adaptive Mesh Refinement). MG allows for an efficient ad accurate evaluation of the gravitational field, while AMR provides high resolution computations exactly where needed. GAMMS is an open source code which takes advantage of the open source, based upon MPI, DAGH parallel library. Our code can be easily integrated with both N-body and fluid-dynamics code, in order to perform high resolution astrophysical simulations.
Many astrophysical problems deal with the computation of gravitational
forces.
Usually, this task can be performed only by computer simulations.
A large computational domain is to be treated,
and good spatial resolution is required.
Cosmological problems are distinguished examples.
A cosmological structure formation process involves an extremely large
dynamical range.
As large as the universe volumes are featured (![]() Mpc), yet
one must solve the problem of resolving star formation regions in galaxies,
which are typically at the 1 pc scale.
The spatial dynamical range per dimension required is as large as
Mpc), yet
one must solve the problem of resolving star formation regions in galaxies,
which are typically at the 1 pc scale.
The spatial dynamical range per dimension required is as large as
![]() , well beyond the maximum value,
, well beyond the maximum value, ![]() , that nowadays
can be managed on supercomputers.
, that nowadays
can be managed on supercomputers.
A solution to this range problem relies upon combining
the Multigrid (MG) method
(Brandt 1977, Suisalu & Saar 1995)
with local refinement techniques.
Multigrid solves differential equations
using a set of multilevel grids,
for an optimal ![]() computational cost.
Moreover, MG allows for efficiently tracking
errors, and it can be effectively combined with local refinement techniques.
We exploited
Adaptive Mesh Refinement (AMR), which allows for
dynamically defining and managing the computational
meshes;
they can be either refined, where high resolution is required, or
coarsened, where low resolution is enough.
Hence, the treatment of any interesting
physical process is performed at its proper spatial resolution,
whereas it would be too expensive by uniform grid treatment.
computational cost.
Moreover, MG allows for efficiently tracking
errors, and it can be effectively combined with local refinement techniques.
We exploited
Adaptive Mesh Refinement (AMR), which allows for
dynamically defining and managing the computational
meshes;
they can be either refined, where high resolution is required, or
coarsened, where low resolution is enough.
Hence, the treatment of any interesting
physical process is performed at its proper spatial resolution,
whereas it would be too expensive by uniform grid treatment.
The ensuing code, GAMMS (Gravitational Adaptive Mesh Multigrid Solver) is described in the sequel.
Let us consider Poisson's equation
The linear system is solved using a relaxation method, which
computes ![]() on each node by considering only the
adjacent ones, hence they
efficiently reduce the error only at high frequency modes,
while performing bad on smooth error components,
which live at a whole domain scale.
Slow convergence would emerge.
On the other hand, large scale smooth errors
can be read as local errors on
coarser grids, where they can be smoothed out using the same
relaxation technique.
Hence, several discretization levels of the
same continuous problem can be used to smooth out errors
at different scales.
This is the basic idea of MG,
which enrolls a hierarchy of coarser and coarser
grids to reduce the error at larger and
larger scales, thus providing fast convergence.
Traversing the hierarchy is called performing a V-cycle.
Figure 1 sketches a sample V-cycle.
on each node by considering only the
adjacent ones, hence they
efficiently reduce the error only at high frequency modes,
while performing bad on smooth error components,
which live at a whole domain scale.
Slow convergence would emerge.
On the other hand, large scale smooth errors
can be read as local errors on
coarser grids, where they can be smoothed out using the same
relaxation technique.
Hence, several discretization levels of the
same continuous problem can be used to smooth out errors
at different scales.
This is the basic idea of MG,
which enrolls a hierarchy of coarser and coarser
grids to reduce the error at larger and
larger scales, thus providing fast convergence.
Traversing the hierarchy is called performing a V-cycle.
Figure 1 sketches a sample V-cycle.
To go up and down along the grid hierarchy, two problem-dependent operators must be devised: a restriction operator, which allows to map onto a coarser grid any GF given on a fine grid; a prolongation operator, in order to map any GF given on a coarse grid, onto a one-level higher, finer grid.
The problem is eventually
solved only at a coarse grid level, the upper levels being
resolved by exploiting the prolongation operator.
Since coarsening produce
smaller algebraic systems, the computational cost
of solving a linear system on a coarse grid is low.
One can prove that MG has an ![]() computational cost,
computational cost,
![]() being the number of grid nodes.
MG can also easily manage locally refined grids.
being the number of grid nodes.
MG can also easily manage locally refined grids.
The AMR technique
(Berger & Oliger 1984)
allows for refining any region in the computational volume, by
building a nonuniform grid, which is the
union of uniform sub-grids ![]() ,...,
,...,![]() , each one featuring its
mesh size
, each one featuring its
mesh size
![]() ,
,
![]() ;
;
![]() being a given value.
being a given value.
Inside our GAMMS code, each adaptive mesh is built and controlled
using the DAGH (Distributed
Adaptive Grid Hierarchy) library
(see http://www.caip.rutgers.edu/~parashar/DAGH).
DAGH provides data abstractions and all the tools required in order to define
and manage grid values on a nonuniform, dynamically evolving mesh.
DAGH is an open source package and features a parallel implementation,
based upon a standard MPI library.
At the present stage, MG and AMR are not fully combined. We tested them separately.
Tests on our MG implementation proved that the algorithm converges in few relaxation sweeps, when a moderate number of V-cycles is performed. Figure 2 shows that the computational cost of our MG code increases linearly with the number of grid points, as theory predicts.
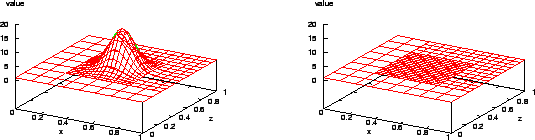 |
Tests on our AMR code show that it can efficiently handle an adaptive mesh. Figure 3 shows a three-level local refinement driven by a Gaussian function, which was set initially on the coarsest, uniform grid. The grid was locally refined according to the magnitude of the derivative: larger magnitude requires finer resolution.
A detailed description of the codes and tests can be found in the Degree Thesis of R. Peruzzo (2003) and U. Zuccon (2003).
Brandt A., Math. Comp., 1977, 31, 333
Suisalu I., Saar E., 1995, MNRAS, 274, 287S
Berger M. J., Oliger J., 1984, J. Comp. Phys., 484, 54
Peruzzo R."Implementazione Object Orented Implementation of the AMR technique to calculate the gravitational field", Degree Thesis, 2003, University of Venice
Zuccon U. "Implementation of a 3D algorithm to calculate the gravitational field" Degree Thesis, 2003, University of Venice