ADASS 2003 Conference Proceedings

We discuss a number of new and upcoming programs in NEMO software toolkit that can be used to fit particle distributions (e.g. from N-body simulations, but also grid based simulations) to observations. Non-linear fitting, especially those with many complex parameters, present themselves with many problems. Genetic programming is one such solution. The fitting programs in this paper are mainly applicable to analyzing velocity fields of individual galaxies and interacting galaxies, and apply new techniques such as genetic programming. We also discuss how these packages can be of use to a theory component in a Virtual Observatory.

1. Introduction

Detailed mass models for galaxies give important clues about their possible past formation and future evolution. The observed light distribution gives many clues about the different components disk galaxies seem to be made up of (bulge, disk, bars etc.), though it was not until the velocity field of tracer material such as HI in the outer parts of disk galaxies was studied (see Sofue & Rubin, 2001, for an excellent recent review), that an unseen component was postulated to exist. The earliest velocity observations were mostly single optical slit spectra, and with the assumption of circular orbits the inversion from a rotation curve to a mass distribution was fairly straightforward. With different components and degrees of flattening (assumed!) this is still a non-linear fitting process with typically 4 parameters, and traditional non-linear optimization techniques can work well on some of these problems. Charbonneau (1995) introduced our community to an approach using genetic programming (see also Gomez et al, 2004). With the advent of radio and Fabry-Perot interferometers, and more recently Integrated Field Spectrometers, two dimensional velocities fields are now commonplace and accurately measured. This made it possible to fit a single rotation curve to the whole velocity field (e.g. van Moorsel & Wells 1985) or alternatively for each ``ring'' in the disk independently fit the position angle, inclination and rotation speed. The geometry itself requires 5 fitting parameters (position angle, inclination, X-center, Y-center and V-center), whereas the former adds an N-parameter (typically 4 parameters) family of rotation curves, and the latter a non-parametric lookup table for a rotation curve as function of radius.

Beam smearing can add a large uncertainty to the fitted rotation curve. Add to this the complexity of non-circular motions, such as due to bars and spiral arms (see e.g. Barnes & Sellwood 2003) and you have a recipe for disaster. One can thus see that inverting the observations to get to the original intrinsic dynamics can be tricky. Takamiya & Sofue (2002) have recently attempted to iterate over a position-velocity diagram (PVD) and thus recover the intrinsic rotation curve that is consistent with a that 2-dimensional PVD. Swaters (1999) on the other hand started a full blown 3-dimensional recovery, by simulating the observation and comparing the results to the observations.

2. Velocity Fields

Velocity fields are commonly derived from a datacube by fitting gaussians or taking moments. They both suffer from biases in the computed velocity, depending on the surface density distribution and amount of beam smearing. The result is that the velocity errors are not gaussian, which invalidates any normal fitting procedure.

**Figure 1:** Left: Tilted ring fit with only rotation speed, inclination and position angle of the disk fitted. Notice the bad fit in the inner portions. Right: improvement in the kinematic determination of the inclination of a disk galaxy of the functional disk fit (FS) vs. the tilted ring (TR) method. The upper panel shows the ratio of the formal error bars to be around 10 in the inner portions to 5 in the outer disk.
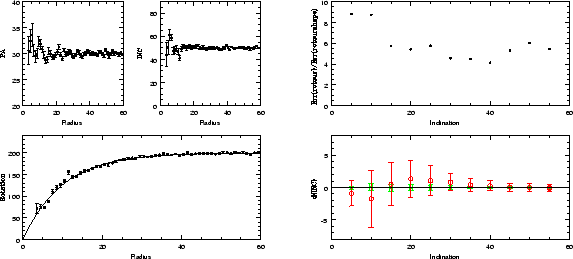
$\begin{figure} \plottwo{P7-6_f1a.ps}{P7-6_f1b.ps} \end{figure}$

Traditionally galaxy disk modeling is done by either fitting the velocity in a set of ring (tilted ring fitting, TR), see e.g. Begeman (1989), or by fitting a functional form to the rotation curve in the disk (FD), see e.g. van Moorsel & Wells (1985). The TR method (first implemented in GIPSY's rotcur program) is more flexible, since it allows for geometry to vary as function of radius, and thus handle more general cases like warped galaxies. But it has a drawback that in each ring the "rotation curve" does not vary as function of radius, making it look like a step function. In addition to the small number of points in rings near the center, the velocity gradients in those rings can clearly not be neglected (see Figure 1, where some rings near the center did not even converge in this particular example). The FD method (first implemented in AIPS' vel program, allows for a more accurate determination of the inclination (the kinematic inclination). This is illustrated in the simulations of NEMO's rotcur and rotcurfit in Figure 1.

**Figure 2:** Tilted ring fitting of simulated disks. From top left to bottom right the fitted values of intrinsic and observed rotation speed, the position angle and inclination of the disk are shown. The center and systemic velocity were fixed at the known answer in this example. The solid line represents the correct answer. Notice that this particular example has created a warped galaxy!
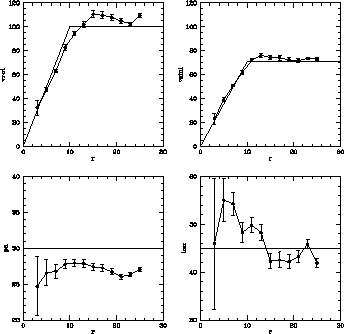$\begin{figure} \epsscale{0.6} \plotone{P7-6_f2.ps} \end{figure}$

3. BIMA Simulations of Velocity Fields

As an example of a more complex simulation, we took simulated observations of a disk galaxy with the BIMA interferometer. Since such interferometers create maps with limited spatial information, advanced deconvolution techniques are necessary to obtain the true distribution of the gas in a datacube. Because a rotating disk has a different distribution in the cube depending on the recession velocity, deconvolution can be biased if the observation did not have an optimal distribution of antenna pair orientations, e.g. because the observation was a snapshot, the galaxy was at an unfavorable declination, or if the array configuration was not optimal. The simulated observations, modeled after the BIMA SONG survey, were performed with MIRIAD (Sault et al, 1995), including their velocity fields. These were then analyzed with the tilted ring fitting method in NEMO, of which the results for one particular case are summarized in Figure 2.

4. Genetic Programming

An excellent introduction to Genetic Programming can be found in Charbonneau (1995)'s paper, and references therein. Genetic programming also do not need to know the derivatives of the cost function w.r.t. its parameters, which can not only be a huge save, but also practically impossible in other situations (see e.g. Theis & Kohle 2001 for an application to fit galaxy-galaxy interactions). Our simulations with a complex dynamical model, the distribution of gas and beam smearing has a large number of complex parameters which do seem to be ideally suited to this approach, and work work on this is in progress.

5. Theory in a Virtual Observatory

Packages like NEMO and Starlab are ideally suited to help integrating theory and observations in a Virtual Observatory (see also Teuben et al. 2002). One can either find (or re-compute) models that should represent observations, run them through a set of programs that simulate an observation, and compare the results to a true observation, or simulate the effects of an observation.

Acknowledgments

References

Sault, R. J., Teuben, P. J. & Wright, M. C. H., 1995, in ASP Conf. Ser., Vol. 77, Astronomical Data Analysis Software and Systems IV, ed. R. A. Shaw, H. E. Payne, & J. J. E. Hayes (San Francisco: ASP), 433

Teuben, P.J. 1995, in ASP Conf. Ser., Vol. 77, Astronomical Data Analysis Software and Systems IV, ed. R. A. Shaw, H. E. Payne, & J. J. E. Hayes (San Francisco: ASP), 398

Genetic Programming and other fitting techniques in Galactic Dynamics

Abstract: