Boxiness, the fourth order cosine coefficient of Fourier harmonics, is known to be an important photometric parameters in study of early type galaxies (e.g. Kormendy & Djorgovski 1989) The boxiness parameter is, however, not measured in recent huge survey data. One of the reason would be the fact that standard boxiness measurement process is complicated and takes time; fit ellipse, take residual, iterate if needed, and fit trigonometric functions. Another reason could be that fitting method is usually not full-automatic, and requires manual interactive operation, which disables us from constructing pipeline analysis.
About 2nd-order Fourier components, such as major/minor axis, many surface photometry packages estimate the parameters from 2nd-order Cartesian moments (e.g. Stobie 1980), and therefore automatic measurement is implemented. Extending the idea, I developed a procedure to estimate the boxiness from 2nd and 4th order non-weighted Cartesian moments.
In this study, I follow the formalization of
the general ellipse by Stobie (1980);
setting original coordinate as (x,y),
and coordinate along the major and minor axis of
the best fit ellipse as (X,Y),
| (1) | |||
| (2) |
| (3) |
I define a moment of a shape as non-weighted,
![]() .
With such moment, estimated major/minor axis can be written as
.
With such moment, estimated major/minor axis can be written as
| (5) |
| (6) |
As ![]() is usually less than 10% (e.g. Bender et al. 1988),
one can neglect
is usually less than 10% (e.g. Bender et al. 1988),
one can neglect ![]() and approximate as
and approximate as
![]() .
With this approximation,
.
With this approximation, ![]() of Eqn. (4) is written as
of Eqn. (4) is written as
| (8) |
The Eqn. 7 is implemented in standard C
as a code for measuring boxiness profile, ![]() .
Rapid flooding method (Treuenfels 1994) is adopted
for extracting isophotal shape profile.
And in moment calculation, ``single visit with
temporal mean method'' is adopted, which uses recurrence formulae;
.
Rapid flooding method (Treuenfels 1994) is adopted
for extracting isophotal shape profile.
And in moment calculation, ``single visit with
temporal mean method'' is adopted, which uses recurrence formulae;
![]() .
As rapid flooding method visit once for each pixel,
and single visit with temporal mean method can
calculate moment by the single visit,
the combination succeeds in quick boxiness estimation.
For boxiness estimation only, the code is
about 20 times faster than IRAF/STSDAS
ellipse task (Busko 1996) tested on Solaris/SPARC
architecture.
.
As rapid flooding method visit once for each pixel,
and single visit with temporal mean method can
calculate moment by the single visit,
the combination succeeds in quick boxiness estimation.
For boxiness estimation only, the code is
about 20 times faster than IRAF/STSDAS
ellipse task (Busko 1996) tested on Solaris/SPARC
architecture.
The error is estimated by applying the code to simulated images.
For large (![]() ) images,
relative error of
) images,
relative error of ![]() is always less than 10%,
with no systematic error with rotation angle.
All except rounder (Q=0.9) image have
absolute error less than 0.001.
For smaller images, error correlates with
is always less than 10%,
with no systematic error with rotation angle.
All except rounder (Q=0.9) image have
absolute error less than 0.001.
For smaller images, error correlates with
![]() .
Error is smaller than 0.005(rms) for
.
Error is smaller than 0.005(rms) for ![]() pix,
and smaller than 0.01(rms) for
pix,
and smaller than 0.01(rms) for ![]() pix.
pix.
The implementation is applied to real image of
23 E/S0 galaxies taken from Frei (1996) R-band data.
Our result is consistent with other studies
within relative error of 10% or absolute error of 0.01.
The accuracy is as expected from model analysis,
and enough for boxy/disky discrimination.
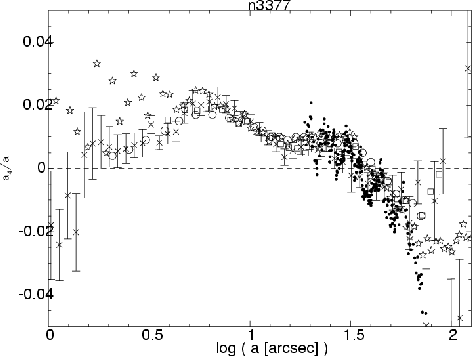
Figure 1 shows an example of the result.
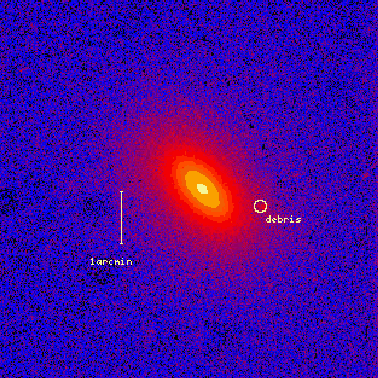
Some inconsistency is found around log(a)![]() 1.8,
where star debris is seen in the image.
It could be the difference of the image quality,
preprocessing of the image, or post-processing of
the boxiness profile.
1.8,
where star debris is seen in the image.
It could be the difference of the image quality,
preprocessing of the image, or post-processing of
the boxiness profile.
As a next step, I plan to investigate flux-weighted moments, preprocessing (e.g. Unsharpmasking) of images, and interpolation of internal parts or interpolation of moments at small radii.
 |
 |
Bender, R., Döbereiner, S. & Möllenhoff, C. 1988, A&AS, 74, 385
Busko, I. 1996, in ASP Conf. Ser., Vol. 101, Astronomical Data Analysis Software and Systems V, ed. G. H. Jacoby & J. Barnes (San Francisco: ASP), 139
Frei, Z., Guhathakurta, P., Gunn, J. E. & Tyson, J. A. 1996, AJ, 111, 174
Jedrzejewski, R. I. 1987, MNRAS, 226, 747
Kormendy, J. & Djorgovski, S. 1989, ARA&A, 27 235
Milvang-Jensen, B. & Jørgensen, I. 1999, BaltA, 8, 535
Michard, R. & Marchal, J. 1994, A&AS, 105, 481
Peletier, R. F., Davies, R. L., Illingworth, G. D., Davies, L. E. & Cawson, M. 1990, AJ, 100, 1091
Stobie, R. S. 1980, JBIS, 33, 323
Treuenfels, A. 1994, C Users Journal, 12, 8, 39