Next: Non-linear transient models and transient corrections methods for IR low-background photo-detectors
Up: Surveys, Archives & VO
Previous: Image Centering with a Maximum Likelihood Estimator: Application to Infrared Astronomical imaging
Table of Contents -
Subject Index -
Author Index -
Search -
PS reprint -
PDF reprint
Grumm, D. & Casertano, S. 2003, in ASP Conf. Ser., Vol. 314 Astronomical Data
Analysis Software and Systems XIII, eds. F. Ochsenbein, M. Allen, & D. Egret (San Francisco: ASP), 562
Refinements to the Iterative Self-Calibration Program for the SIRTF GOODS Legacy Project
David Grumm, Stefano Casertano
Space Telescope Science Institute
Abstract:
A self-calibration program for processing data from the upcoming SIRTF GOODS Legacy Project has
been developed to derive the sky and flat field for idealized data. The actual on-orbit data will
doubtless suffer from geometric distortion and cosmic rays at some level, while calibration is
required to simultaneously derive the sky and flat field in the presence of these effects to a level of
better than a part in 10,000. Because this translates to the requirement that the calibration be
shot-noise limited, routines to remove both of these effects within an iterative version of the
self-calibration code have been developed. Results of tests using these routines will be discussed.
The algorithm applied to correct geometric distortion is a new method that allows arbitrary
transformations with sub-pixel shifts - a substantial improvement over clipping techniques and
other distortion removal techniques currently in use. This enhanced self-calibration program is
general, allowing it to be used for high-quality calibration of data from JWST and other future
missions. The development of these methods demonstrates the feasibility and effectiveness of
enhancing the powerful technique of iterative self-calibration to reduce or eliminate anticipated
effects in realistic data.
The original iterative self-calibration program has been described in the poster ``Self Calibration for
the GOODS Legacy Project'' presented at ADASS 2002 (Grumm & Casertano 2003) . In short, the
iterative routine simultaneously
solves for the sky and gain for ideal data (integer pixel shifts, no geometric distortion, no cosmic rays).
The new refinements to this program as described here were tested on data generated by the
simulators for SIRTF's IRAC and MIPS instruments, as on-orbit data was not yet available.
Geometric distortion will be present at some level for both the IRAC and MIPS instruments on SIRTF.
For MIPS, this distortion has been measured, and is on the order of one pixel at the edge of the 128x128
array. Distortion was added to the simulated data using
the ``drizzle'' routine described later. We have investigated two types of algorithms for the
self-calibration to remove the distortion. In the first, outlier clipping is done so that the effect of the
distortion will be reduced because the pixels in the brightest sources (which would be expected to
have the largest effect in the self-calibration) will be masked. In the second, the variable pixel
linear reconstruction task ``drizzle'' (Hook & Fruchter 1997, Fruchter & Hook 2002) is used to effectively
remove the distortion .
As this method makes use of all of the data, it is preferable in instances where the distortion is well known
and characterized. The results of routines applying each of these two methods are discussed.
Clipping will reduce the impact of the brightest sources on the self calibration, and does not require
a quantitative characterization of the distortion. In this approach, an initial flat field was determined
by running the program for several iterations. The data was then flat-fielded, and data pixels
exceeding a given threshold were masked. The self-calibration program was then run on this
masked dataset until convergence. The threshold was set by specifying a value that exceeds the
mean by a given fractional amount. In this way the rms of the derived flat field was determined as a
function of the threshold. It would be expected that as the threshold is reduced the rms would at
first improve due to the lower impact of the distortion, and then worsen due to an insufficient
number of available pixels.
For a distorted set of noiseless images, the rms of the gain image was minimized with a value of
4.55E-5 when the threshold was set to 2.5%
above the flat-fielded average, at which point 2%
of the
pixels were masked. Without masking, the rms is 2.62E-4. For a set with shot noise, the rms had a
shallow minimum of 4.77E-4 when the threshold was set 1.5%
above the mean. Without masking
the rms is 5.37E-4. The results are shown in Table 1; the `base' rms pertains to the fit without
clipping, and the efficiency shown in brackets is the fraction of equivalent noise removed. Results
for undistorted datasets are shown for comparison.
![\begin{deluxetable}{ccccc}
\scriptsize\tablecaption{Clipping and drizzle results...
...s & 5.37E-4 & 4.77E-4 [0.44] & 4.11E-4 [0.92] \nl
\enddata
\par\end{deluxetable}](img1.gif)
In instances where the distortion is well known and characterized, the variable pixel linear
reconstruction task ``drizzle'' is preferable to remove the distortion. The data is projected onto the
sky using drizzle, and the inverse routine ``blot'' is used to project the sky back to the detector. The
distortion is specified by a distortion coefficient file, which allows fairly general (cubic and higher
order polynomial) specification. For the same datasets as were used for the clipping routine, the
results are shown in Table 1. The drizzle-based self-calibration can be seen to better remove the distortion,
even in the presence of noise.
As cosmic rays will appear in the data at some level, routines to reject them were developed, based on
the assumption that they may not be completely removed by the standard pipeline. To simulate
cosmic rays within the data, templates based on ground-level data containing cosmic rays were used.
A typical template contains several dozen cosmic rays. Cosmic rays are rejected using an outlier
rejection scheme as follows:
- data containing the cosmic rays are run through the self-calibration routine.
- from the derived sky and gain, a 2nd set of observations is created.
- pixels in this 2nd observation set that differ from those in the original observations by more
than
a defined threshold are considered pixels containing cosmic rays, so are masked; neighboring pixels
are also masked, creating a 3rd observation set.
- the 3rd observation set is input to the self-calibration routine.
The results of the rejection routines on undistorted datasets with and without shot noise are
summarized in Table 2. The threshold value used for rejection was
 ), with
), with 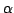 =3.0 and
=3.0 and 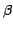 =0.01. From the 3 noiseless cases shown, it can be seen
that 96%
of the equivalent noise (additional rms due to cosmic rays) is removed.
=0.01. From the 3 noiseless cases shown, it can be seen
that 96%
of the equivalent noise (additional rms due to cosmic rays) is removed.
![\begin{deluxetable}{ccccc}
\scriptsize\tablecaption{Cosmic Ray rejection results...
...E-4 & NA \nl
Yes & Yes & 2.43E-4 & 2.09E-4 [0.81] \nl
\enddata
\end{deluxetable}](img5.gif)
The results of simultaneously using both the distortion-removal and rejection routines are shown in Table 3
for all combinations of shot noise, cosmic rays, and added distortion for 720-frame datasets. For cases with
distorted datasets, the distortion removal routine was used.
![\begin{deluxetable}{cccccc}
\scriptsize\tablecaption{Cosmic Ray rejection result...
...NA \nl
Yes & Yes & Yes & 2.43E-4 & 2.08E-4 [0.85] \nl
\enddata
\end{deluxetable}](img6.gif)
Tests using realistic simulated SIRTF data show that if geometric distortion is well characterized, it can be
removed by the drizzle-based self-calibration to almost the shot-noise level. If the distortion has not been
quantified, the use of clipping can reduce the effect of the distortion by roughly half. The use of an outlier
rejection method within the self-calibration allows cosmic rays to be rejected to nearly the shot-noise level.
Currently we are investigating a low-level aliasing in some of our results. It is evident as alternating high
and low pixels in the derived sky and gain, and is most noticeable in areas of the sky having relatively low
exposure. This aliasing seems to be due to the combination of undersampling and the iterative nature of the
algorithm. Various methods are being investigated to eliminate or reduce this effect.
Acknowledgments
The authors would like to thank Richard Hook and the other members of the GOODS team.
References
Fruchter, A.S. & Hook R.N. 2002, PASP, 114, 144
Grumm, D. & Casertano, S. 2003, in ASP Conf. Ser., Vol. 295, Astronomical Data Analysis Software and Systems
XII,
ed. H. E. Payne, R. I. Jedrzejewski, & R. N. Hook (San Francisco: ASP), xii:P7-6199
Hook, R. & Fruchter, A.
1997, in ASP Conf. Ser., Vol. 125, Astronomical Data Analysis
Software and Systems VI, ed. G. Hunt & H. E. Payne
(San Francisco: ASP), vi:P9-6147
© Copyright 2004 Astronomical Society of the Pacific, 390 Ashton Avenue, San Francisco, California 94112, USA
Next: Non-linear transient models and transient corrections methods for IR low-background photo-detectors
Up: Surveys, Archives & VO
Previous: Image Centering with a Maximum Likelihood Estimator: Application to Infrared Astronomical imaging
Table of Contents -
Subject Index -
Author Index -
Search -
PS reprint -
PDF reprint
![\begin{deluxetable}{ccccc}
\scriptsize\tablecaption{Clipping and drizzle results...
...s & 5.37E-4 & 4.77E-4 [0.44] & 4.11E-4 [0.92] \nl
\enddata
\par\end{deluxetable}](img1.gif)
![\begin{deluxetable}{ccccc}
\scriptsize\tablecaption{Cosmic Ray rejection results...
...E-4 & NA \nl
Yes & Yes & 2.43E-4 & 2.09E-4 [0.81] \nl
\enddata
\end{deluxetable}](img5.gif)