Next: Refinements to the Iterative Self-Calibration Program for the SIRTF GOODS Legacy Project
Up: Surveys, Archives & VO
Previous: JPEG 2000 Compression for the Downlink and Archiving of Astronomical Data
Table of Contents -
Subject Index -
Author Index -
Search -
PS reprint -
PDF reprint
Gratadour, D., Mugnier, L. M., & Rouan, D. 2003, in ASP Conf. Ser., Vol. 314 Astronomical Data
Analysis Software and Systems XIII, eds. F. Ochsenbein, M. Allen, & D. Egret (San Francisco: ASP), 558
Image Centering with a Maximum Likelihood Estimator: Application to Infrared Astronomical imaging
Damien Gratadour
DOTA / ONERA, BP 72, 92322 Châtillon cedex, France.
Laurent M. Mugnier
LESIA / Observatoire de Paris-Meudon, 92195 Meudon, France
Daniel Rouan
DOTA / ONERA, BP 72, 92322 Châtillon cedex, France.
Abstract:
We present a new, Maximum Likelihood (ML) based,
method for the estimation of the shift between two images. It notably outperforms the classical cross-correlation method especially in the case of low photon levels. Moreover, it is arbitrarily subpixel, without any resampling of the image, through the maximisation of a criterion.
The method was tested with simulations and was applied to the case of infrared astronomical imaging where the signal is usually very weak. We have also extended our method to the joint estimation of the shifts in a sequence of N images, and preliminary results are presented in last section.
An accurate centering of a sequence of images is mandatory in thermal IR astrophysics to increase SNR while preserving the resolution of an instrument. A classical method to estimate the translation parameters is the linear
cross-correlation of noisy images with a reference
(Vanderlugt 1964, Kumar et al. 1992). Downie and Walkup
(1994) showed that taking into account the noise
statistic can greatly improve the accuracy. Carfantan & Rougé have studied
the case of the subpixel estimation of the maximum of the intercorrelation of
two images with various interpolation for a stationnary gaussian noise (Carfantan and Rougé 2001). Finally Guillaume et al. have studied the pixel accurate shift estimation problem in the case of poissonian noise at low photon level (Guillaume et al. 1998).
We have developped a new, Maximum Likelihood (ML) based,
method for the estimation of the shift between two images. It is arbitrarily subpixel, without any resampling of the image, through the maximisation of a criterion.
We describe in section 2 the theoretical basis of the method. Then in section 3, we present the results obtained with simulated images for different types of noise (pure gaussian additive or mixture of stationnary gaussian and poissonian noise). Results on real data are presented in section 4. We have also extended our method to the joint estimation of the shifts in a sequence of N images, and preliminary results are presented in last section.
If we assume a reference 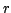 , the intensity at pixel
, the intensity at pixel 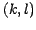 of the
observed translated image
of the
observed translated image 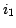 can be written as:
can be written as:
![\begin{displaymath}
i_1(k,l)={\left[r(x,y) \ast \delta(x-x_1,y-y_1)\right]}_{\mbox{\cyr sh}} (k,l)+b_1(k,l)
\end{displaymath}](img4.gif) |
(1) |
where 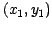 are the translation parameters,
are the translation parameters, 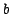 is an
additive noise, and
is an
additive noise, and
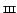 is the sampling operateur. If the image is Nyquist sampled, one can reconstruct, via the Fourier domain, a shifted version of the image for any subpixel shift.
If we approximate the noise in the image, i.e. a mixture of gaussian (detector) and poissonian noise, as a non-stationnary gaussian noise, then the anti log-likelihood of observing an intensity
is the sampling operateur. If the image is Nyquist sampled, one can reconstruct, via the Fourier domain, a shifted version of the image for any subpixel shift.
If we approximate the noise in the image, i.e. a mixture of gaussian (detector) and poissonian noise, as a non-stationnary gaussian noise, then the anti log-likelihood of observing an intensity 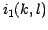 for the
reference intensity
for the
reference intensity 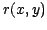 and for the hypothesis
and for the hypothesis
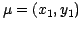 is given by:
is given by:
![\begin{displaymath}
\displaystyle \mathcal{J} (x_1,y_1) =\sum_{k,l}
\frac{1}{2\s...
... \delta(x-x_1,y-y_1)\right]}_{\mbox{\cyr sh}} (k,l)\big\vert^2
\end{displaymath}](img11.gif) |
(2) |
where 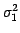 is the noise variance which can be directly
estimated on the image. It is easy to show that, following the two hypothesis of stationnarity of the noise and of periodicity of the reference, the ML estimate of the translation between the two images is the
maximum of the linear cross-correlation of the images. When the reference is not known, one has to consider a noisy frame as a reference.
is the noise variance which can be directly
estimated on the image. It is easy to show that, following the two hypothesis of stationnarity of the noise and of periodicity of the reference, the ML estimate of the translation between the two images is the
maximum of the linear cross-correlation of the images. When the reference is not known, one has to consider a noisy frame as a reference.
![\begin{displaymath}
i_1(k,l)={\left[i_0(x,y)\ast \delta(x-x_1,y-y_1)\right]}_{\mbox{\cyr sh}}+b(k,l)
\end{displaymath}](img13.gif) |
(3) |
Where 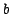 includes both the noise in the image used as a reference and the noise in the image to be recentered. Then the anti log-likelihood to be minimize has the same
expression as in equation 2 changing
includes both the noise in the image used as a reference and the noise in the image to be recentered. Then the anti log-likelihood to be minimize has the same
expression as in equation 2 changing 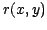 into
into 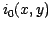 and
and
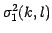 into
into
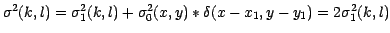 :
:
![\begin{displaymath}
\displaystyle \mathcal{J} (x_1,y_1) =\sum_{k,l}
\frac{1}{4\s...
...(x,y)-{\left[i_0(x-x_1,y-y_1)\right]}_{\mbox{\cyr sh}}\vert^2
\end{displaymath}](img17.gif) |
(4) |
To find the minimum of this criterion, we used a gradient type
adaptive step minimization algorithm, issued from a collaboration
of our team with the Groupe des Problemes Inverses at Laboratoire
des Signaux et Systemes (GPI 1997). However, one has to notice that the
criterion, in the case of unknown reference and considering the real noise
variance contains a lot of local minima. This make the minimization difficult
and so should decrease the performance of the method in this case.
The method has been tested with
simulations in the case of
a mixture of gaussian (detector) and poissonian
noise.
The gaussian noise variance is constant (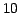 ) and the photon level in the images ranges from
) and the photon level in the images ranges from 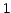 to
to 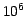 . The cross-correlation of the two images is interpolated around its maximum to provide a sub-pixel estimation.
In the case of the known reference, our method, considering a constant noise variance, outperforms the cross-correlation at very low photon level (i.e. number of photons smaller or equal to variance of the detector noise). When we consider the real noise variance, our method gives more accurate results and slightly outperforms the cross-correlation at high photon levels.
. The cross-correlation of the two images is interpolated around its maximum to provide a sub-pixel estimation.
In the case of the known reference, our method, considering a constant noise variance, outperforms the cross-correlation at very low photon level (i.e. number of photons smaller or equal to variance of the detector noise). When we consider the real noise variance, our method gives more accurate results and slightly outperforms the cross-correlation at high photon levels.
In the case of an unknown reference, the performance of our method is quite identical considering or not the real noise distribution since the criterion contains a lot of local minima in the first case. It notably outperforms the cross-correlation at low photon level and allows subpixel accuracy as soon as the number of photon per pixel is greater than the variance of the detector noise as the accuracy of the interpolated cross correlation is worst than the pixel.
The method has also been tested and used
with a set of raw images of Arp 220 from NAOS-CONICA (NACO) at VLT.
Arp 220 is a typical Ultra Luminous Infrared Galaxy, caracterised by a very powerfull emission in infrared bands but very faint counterpart at the visible wavelengths. NACO is the only adaptive optics system that allows to servo infrared source and so achieve diffraction limited images at a large telescope of such galaxies. A series of 85 images of this galaxy have been aquired in the L-band in March 2003. The background dynamics of each image is around 80000 photons per pixel and the source dynamic at the maximum is around 200 photons per pixel. This is the case where the classical correlation of images is inefficient. Our method allows to recenter each frame with a subpixel accuracy, and so to obtain the image displayed on Fig. 1. The resolution of this image on the sky is about 0.1 ", i.e. diffraction limited for a 8-m telescope in the L-band.
Figure 1:
Adaptive optics image of ARP 220 in the L-band with NACO at VLT. Left image, frames registred with a classical cross-correlation method and averaged, right, frames registred with our algorithm and averaged..
 |
This allows to compare this image to the one obtain with the space telescope in other bands giving insightfull astophysical interpretations (see Gratadour et al. 2003).
If we consider now a series of images 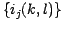 randomly shifted, and if we try to find simultaneously the shift parameters
randomly shifted, and if we try to find simultaneously the shift parameters
 and the reference image
and the reference image 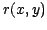 , then the anti log-likelihood can be written as:
, then the anti log-likelihood can be written as:
One can show that minimizing
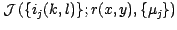 on
on 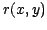 and
and
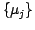 is equivalent to minimize:
is equivalent to minimize:
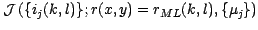 on
on 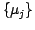 , with:
, with:
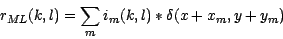 |
(5) |
It can additionnaly be shown (Blanc et al. 2003) that this joint ML solution on 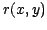 and
and 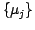 is identical to the ML solution on the sole
is identical to the ML solution on the sole 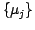 assuming a gaussian prior probability on
assuming a gaussian prior probability on 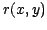 .
The preliminary results show that, as in the previous method (estimation of
the shift between two images) the criterion which considers the real noise
variance contains a lot of local minima. This induce low performance of the
method in this case. But, if we consider a constant noise variance, and we use
the shift estimated with the previous method as guess for the minimization of
this joint criterion, the performance are better in the low photon level
domain (10 to 100).
.
The preliminary results show that, as in the previous method (estimation of
the shift between two images) the criterion which considers the real noise
variance contains a lot of local minima. This induce low performance of the
method in this case. But, if we consider a constant noise variance, and we use
the shift estimated with the previous method as guess for the minimization of
this joint criterion, the performance are better in the low photon level
domain (10 to 100).
No References!
References
Blanc, A. & Mugnier, L. M. & Idier, J. 2003, JOSA A, 20, 6
Carfantan, H. & Rougé, B. 2001, GRETSI XVIII, 849
Downie & Walkup 1994, JOSA A, 11, 1599
Gratadour, D. & Rouan, D. & Clenet, Y. & Gendron, E. &
Lacombe, F. 2003 IAU Symp. 221, 265
Groupe des Problèmes Inverses, ``GPAV une grande oeuvre collective'' internal report, LSS, 1997
Guillaume, M. & Melon, P. & Refregier, P. & Llebaria, A. 1998, JOSA A, 15, 2841
Slocumb, B. & Snyder, D. 1990, Acqu. Track. and Point. IV, 1304, 165
Vander Lugt, A. 1964, IEEE Transactions on information theory, 10, 139
Vijaya Kumar, B. & Dickey F. & DeLaurentis J. 1992, JOSA A, 9, 678
© Copyright 2004 Astronomical Society of the Pacific, 390 Ashton Avenue, San Francisco, California 94112, USA
Next: Refinements to the Iterative Self-Calibration Program for the SIRTF GOODS Legacy Project
Up: Surveys, Archives & VO
Previous: JPEG 2000 Compression for the Downlink and Archiving of Astronomical Data
Table of Contents -
Subject Index -
Author Index -
Search -
PS reprint -
PDF reprint

![\begin{eqnarray*}
\displaystyle \mathcal{J}\left(\{i_j(k,l)\};r(x,y),\{\mu_j\}\r...
...\ast \delta(x-x_m,y-y_m)\big]_{\mbox{\cyr sh}}(k,l) \big\vert^2
\end{eqnarray*}](img24.gif)